6 3 Permutation groups and cyclic groups Example

6. 3 Permutation groups and cyclic groups ¡ Example: Consider the equilateral triangle with vertices 1，2，and 3. Let l 1, l 2, and l 3 be the angle bisectors of the corresponding angles, and let O be their point of intersection。 ¡ Counterclockwise rotation of the triangle about O through 120°, 240°, 360° (0°)

¡ f 2: 1 2，2 3，3 1 ¡ f 3: 1 3，2 1，3 2 ¡ f 1 : 1 1，2 2，3 3 ¡ reflect the lines l 1, l 2, and l 3. ¡ g 1: 1 1，2 3，3 2 ¡ g 2: 1 3，2 2，3 1 ¡ g 3: 1 2，2 1，3 3

¡ 6. 3. 1 Permutation groups ¡ Definition 9: A bijection from a set S to itself is called a permutation of S ¡ Lemma 6. 1：Let S be a set. ¡ (1) Let f and g be two permutations of S. Then the composition of f and g is a permutation of S. ¡ (2) Let f be a permutation of S. Then the inverse of f is a permutation of S.

¡ Theorem 6. 9：Let S be a set. The set of all permutations of S, under the operation of composition of permutations, forms a group A(S). ¡ Proof: Lemma 6. 1 implies that the rule of multiplication is well-defined. ¡ associative. ¡ the identity function from S to S is identity element ¡ The inverse permutation g of f is a permutation of S

¡ Theorem 6. 10: Let S be a finite set with n elements. Then A(S) has n! elements. ¡ Definition 10: The group Sn is the set of permutations of the first n natural numbers. The group is called the symmetric group on n letters, is called also the permutation group.

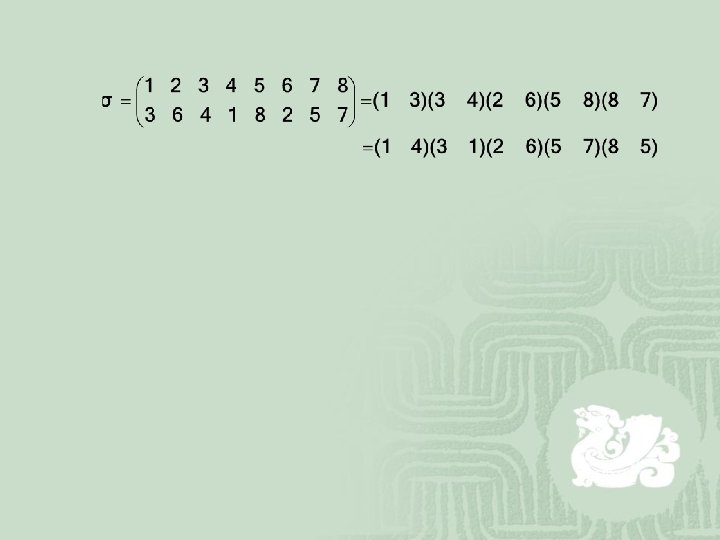
¡ Definition 11: Let |S|=n, and let Sn. We say that is a d-cycle if there are integers i 1; i 2; … ; id such that (i 1) =i 2, (i 2) = i 3, … , and (id) =i 1 and fixes every other integer, i. e.

¡ =(i 1, …, id): ¡ A 2 -cycle is called transposition. ¡ Theorem 6. 11. Let be any element of Sn. Then may be expressed as a product of disjoint cycles. ¡ Corollary 6. 1. Every permutation of Sn is a product of transpositions.

¡ Theorem 6. 12: If a permutation of Sn can be written as a product of an even number of transpositions, then it can never be written as a product of an odd number of transpositions, and conversely. ¡ Definition 12： A permutation of Sn is called even it can be written as a product of an even number of transpositions, and a permutation of Sn is called odd if it can never be written as a product of an odd number of transpositions.

¡ (i 1 i 2 …ik)=(i 1 i 2)(i 2 i 3)…(ik-2 ik-1)(ik-1 ik) ¡ k-1

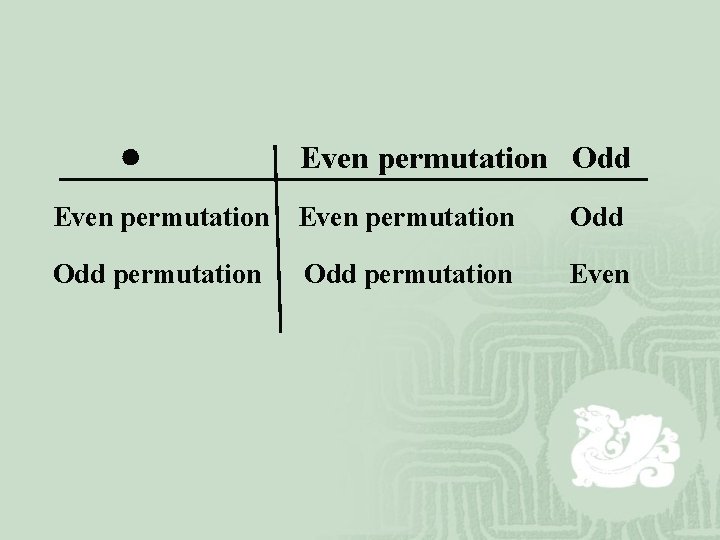
Even permutation Odd permutation Odd permutation Even

Even permutation Odd permutation ¡ Sn= On∪An ¡ On∩An= ¡ [An; ] is a group。 odd permutation Odd permutation Even permutation

¡ Theorem 6. 13: The set of even permutations forms a group, is called the altemating group of degree n and denoted by An. The order of An is n!/2( where n>1) ¡ |An|=? ¡ n=1，|An|=1。 ¡ n>1, ¡ |An|=|On|=n!/2

¡Next: cyclic groups, Subgroups, Normal subgroups ¡Exercise ¡P 212 (Sixth) OR P 195(Fifth) 8, 9, 12, 15, 21