6 3 Electrode Potentials n The producing of






![[H+] = 1 mol/L T = 298 K PH 2 = 1 atm Figure: [H+] = 1 mol/L T = 298 K PH 2 = 1 atm Figure:](https://slidetodoc.com/presentation_image/464b25d950fc24be7e64a833e726c4db/image-9.jpg)
















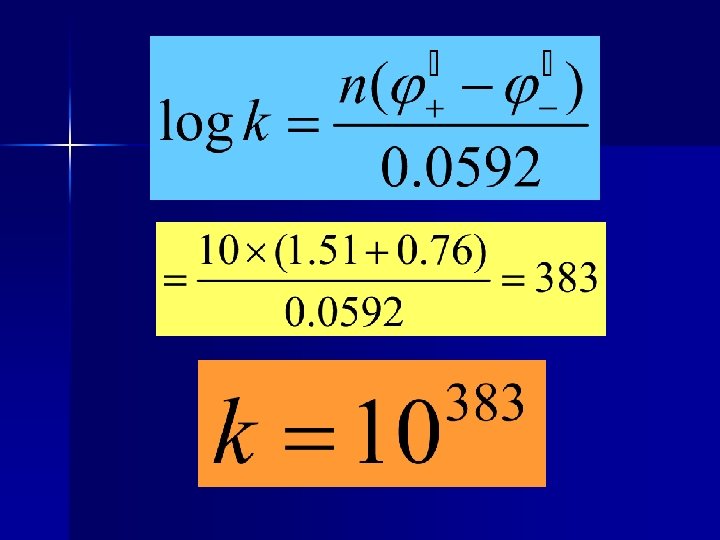















![n=5 O [Mn. O-4][H+]8 =1. 036 (v) n=5 O [Mn. O-4][H+]8 =1. 036 (v)](https://slidetodoc.com/presentation_image/464b25d950fc24be7e64a833e726c4db/image-44.jpg)









![E= φ+-φ-= 0. 0592 log[H+]-(-0. 4189) = 0. 389 V [H+]=0. 3125 mol/L E= φ+-φ-= 0. 0592 log[H+]-(-0. 4189) = 0. 389 V [H+]=0. 3125 mol/L](https://slidetodoc.com/presentation_image/464b25d950fc24be7e64a833e726c4db/image-54.jpg)

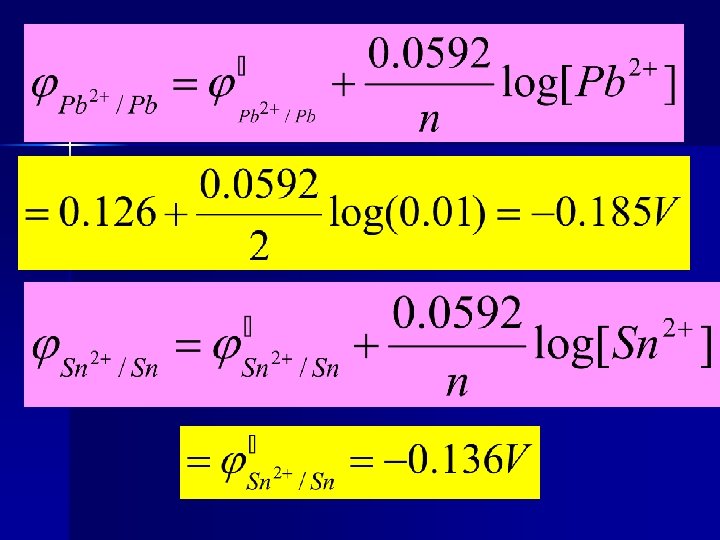










- Slides: 71

6 -3 Electrode Potentials n The producing of Electrode Potentials n Standard electrode potential n Standard hydrogen electrode (SHE) n Application of standard electrode potential

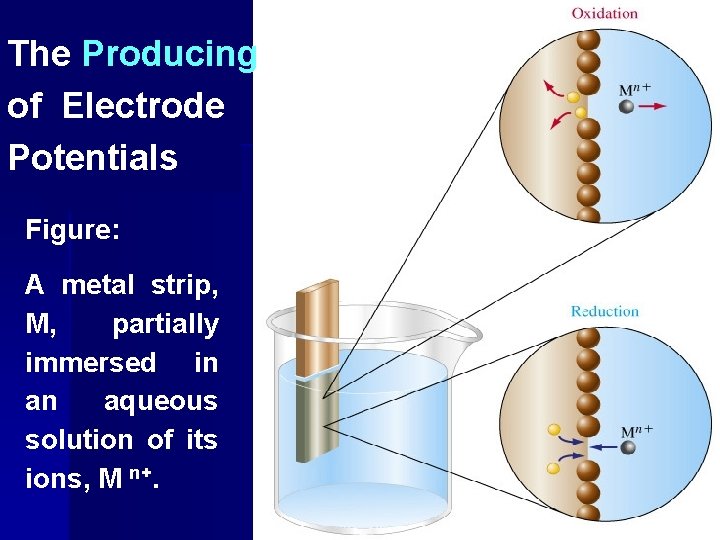
6 -3. 1 Generating Electrode Potentials A strip of mental, M, is called an electrode. An electrode, immersed in a solution containing the metal ions, M n+. Two kinds of interactions are possible between metal atoms on the electrode and metal ions in solution.

The Producing of Electrode Potentials Figure: A metal strip, M, partially immersed in an aqueous solution of its ions, M n+.

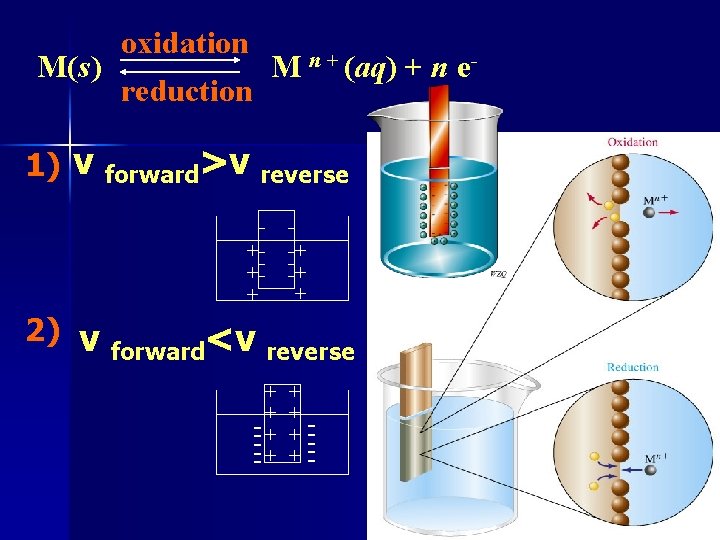
1. A mental atom M on the electrode may lose n electrons and enter the solution as the ion M n+. The metal atom is oxidized. 2. A mental ion M n+ may collide with the electrode, gain n electrons, and be converted to a metal atom M. The ion is reduced. An equilibrium is quickly established between the metal and the solution, which we can represent as oxidation M(s) M n + (a q) + n ereduction

oxidation M(s) M n + (aq) + n ereduction 1) v forward>v reverse + + + 2) v + + + forward<v reverse + + -- + - + + ---

If the oxidation tendency is strong, we expect a very slight negative charge density to accumulate on the electrode. The greater the tendency for the metal to become oxidized, the greater this negative charge density. In turn, the solution develops a very slight buildup in concentration of M n+ ions and a slight positive charge density. If the reduction tendency is strong, we expect the reverse situation-a very slight positive charge density on the electrode and negative charge density in the solution.


6 -3. 2 Determination of Standard Electrode Potentials (Φ°) (-) SHE Standard Electrode (+) E =φ+ - φ- Φ°SHE= 0 =E ● Standard Hydrogen Electrode (SHE)
![H 1 molL T 298 K PH 2 1 atm Figure [H+] = 1 mol/L T = 298 K PH 2 = 1 atm Figure:](https://slidetodoc.com/presentation_image/464b25d950fc24be7e64a833e726c4db/image-9.jpg)
[H+] = 1 mol/L T = 298 K PH 2 = 1 atm Figure: A standard hydrogen electrode. φ°SHE = 0 v H+(l. 0 M)|H 2(1 atm)|Pt

● Standard Electrode Potentials The standard electrode potential, it is designated by a superscript degree sign: φ° A standard electrode refers to an electrode in which the concentration of ions and the pressure of gases are equal to 1 at 25℃.

Examples: Determination of standard zinc electrode potential. (-) Zn Zn 2+(1) E =φ+ - φΦSHE=0 SHE (+) φ°= - E 0

Zn 2+ /Zn versus H+/H 2 Zn/Zn 2+ half-cell combined with a SHE. Eo for the cell is +0. 76 V

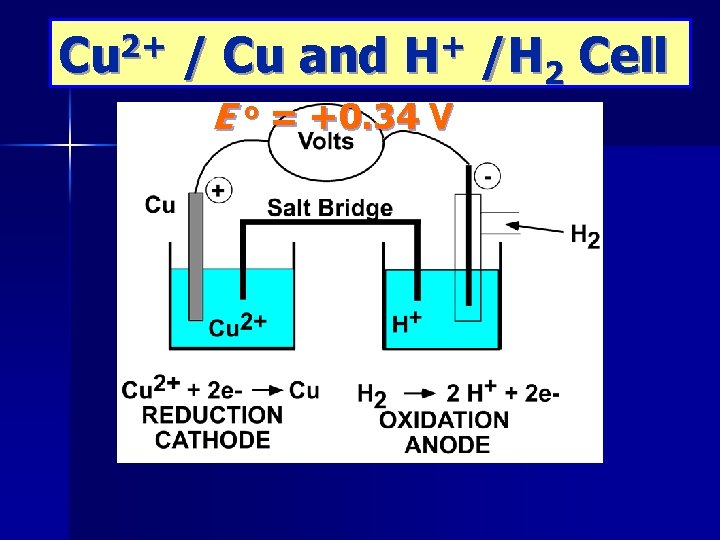
Examples: Determination of standard copper electrode potential. (-) SHE E =φ+ - φΦ°SHE=0 Cu 2+(1) Cu (+) Φ+ ° = E 0

Cu 2+ / Cu and H+ /H 2 Cell E o = +0. 34 V

Cu 2+ (a q) + H 2(g) Cu(s) + 2 H+(a q) n Measured E o = +0. 34 V n n Therefore, Φ°for Cu 2+ + 2 e- Cu is +0. 34 V


6 -3. 3 Applications of Standard Electrode Potentials ● Strength of Oxidizing or Reducing Agents The more positive φ°is, the stronger the oxidizing agent. The more negative φ°is, the stronger the reducing agent.

Example: Oxidizing ability of ion Half-Reaction φ° Cu 2+ + 2 e- Cu + 0. 34 2 H+ + 2 e- H 2 0. 00 Zn 2+ + 2 e- Zn -0. 76 BEST Oxidizing agent ? Cu 2+ BEST Reducing agent ? Zn Reducing ability of element

Example : Which of the following is the most powerful oxidizing agent? Cr 3+(aq) , Br 2(l) , Cu(s) Solution: Look at the values for φ° for the reduction of each of the above species: the largest value is the most powerful oxidizing agent Cr 3+(a q) +3 e → C r(s) φ° = -0. 74 V Cu 2+ + 2 e → Cu(s) φ° = 0. 34 V Br 2(l ) + 2 e → 2 Br -(a q) φ° = +1. 07 V

● E °and Spontaneity ─ Predicting the direction of a redox reaction from the φ° E o > 0, indicates the reaction is spontaneous E o < 0, then the reaction is nonspontaneous Reaction is spontaneous in the reverse direction. E o = 0, at equilibrium E °= φox° - φ red°

If E o is positive, φox° > φ red°, a reaction occurs spontaneously in the forward direction. If E o is negative, φox° < φ red°, a reaction occurs spontaneously in the reverse direction. If E o = 0, φox° =φred°, a reaction is at equilibrium.

Example Consider the reaction Zn 2+(a q)+2 Fe 2+(a q)→ Zn(s)+2 Fe 3+(a q) Does the reaction go spontaneously in the direction indicated, under standard conditions? Solution:

Thus, the electrode potential is greater for Fe 3+/Fe 2+, so that Fe 3+ is the stronger oxidizing agent. The nonspontaneous as written. reaction is

● Calculation of equilibrium constant ─ K , K sp From electrochemistry ΔG°= - n F E° In addition, ΔG°is related to the equilibrium constant (K) through ΔG° = - RT ln K so we conclude that RT ln. K = n. FE°

● Calculation of equilibrium constant ─ K , K sp

Example Calculate the equilibrium constant of the redox reaction at 25℃. 2 Mn. O 4 - (a q) +5 Zn(s) + 16 H+(a q) → 2 Mn 2+ (a q) +5 Zn 2+(a q) + 8 H 2 O ( l ) Solution:
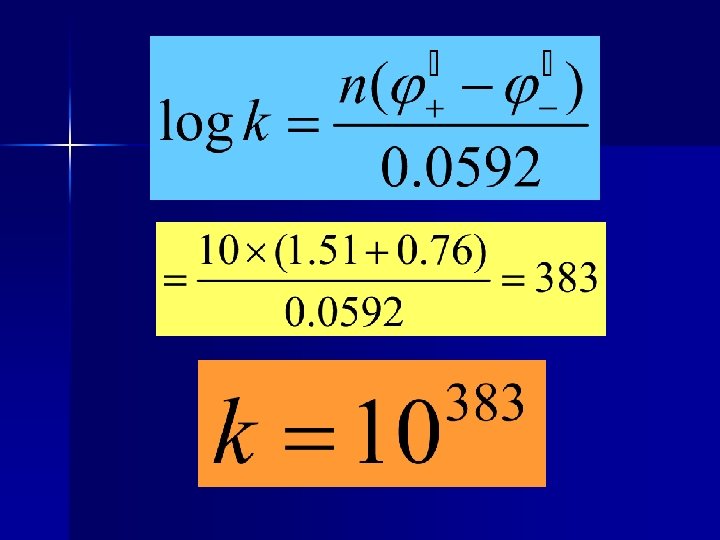

Example Estimate the extent of the following redox reaction at 25℃. Z n + Cu 2+ Z n 2+ + Cu Solution: log k =16. 9× 2 ×(0. 337+0. 76)=37. 18 K = 1. 5 × 10 37 The reaction is very completely from left to right.

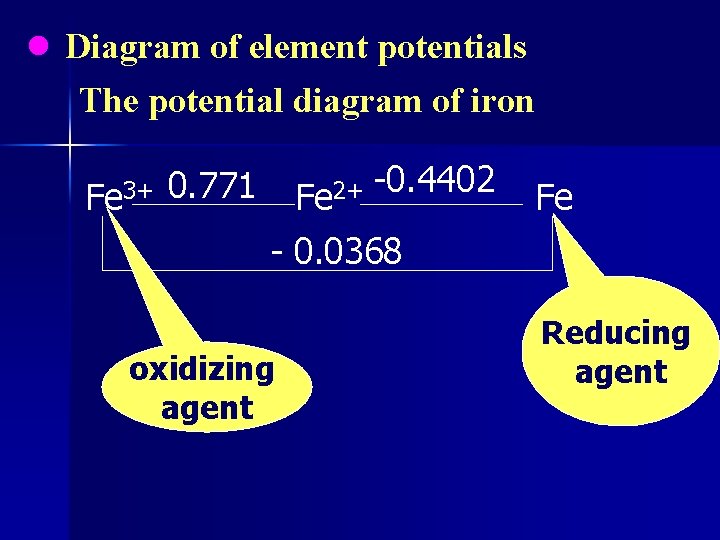
6 -3. 4 Diagram and Its Applications of Element Potentials Fe 3+ + e → Fe 2+ φ°= 0. 77 V Fe 2+ + 2 e → Fe(s) φ° = - 0. 41 V Fe 3+ + 3 e → Fe φ°= - 0. 0368 V Electrode potentials diagram (Diagram of element potentials) Diagrams display the standard reduction potentials (φ°) connecting various oxidation states of an element.

● Diagram of element potentials The potential diagram of iron Fe 3+ 0. 771 Fe 2+ -0. 4402 Fe - 0. 0368 oxidizing agent Reducing agent

● Applications of diagram of element potentials ─ Calculate unknown φ° M 2+ φ1 ° M+ φ2 ° φ3 ° n 3φ3°= n 1φ1°+ n 2φ2° M


Example According to the diagram, calculate Cu 2+ 0. 16 Cu+ ? Solution: 0. 52 Cu

─ Disproportionation is a process in which a single chemical species is both oxidized and reduced. Cu 2+(a q) + e → Cu+(a q) φ°=0. l 6 V Cu+(a q) + e → Cu(s) φ°=0. 52 V 2 Cu+(a q) → Cu 2+(a q) + Cu(s) E °=φ°+ - φ°- =0. 52– 0. 16=0. 36 V

Example Use data in Appendix φ°to decide whether the iron(Ⅱ) ion is unstable with respect to disproportionation under standard conditions. Solution: Fe 3+ + e → Fe 2+ φ° = 0. 770 V Fe 2+ + e → Fe (s) φ°=- 0. 409 V The Fe 2+appears on the left in one and on the right in the other half-reaction. The Fe 2+ ion is stable against disproportionation under standard conditions.

Example Decide whether the following substance can occur disproportionation under standard 2+ conditions: H 2 O , Hg 2 0. 6 2 (1) O 2 (2) Hg 2+ Solution: 8 0. 9 05 H 2 O 2 1. 77 H 2 O Hg 22+ 0. 796 Hg H 2 O 2 can occur disproportionation , but Hg 22+ can not occur disproportionation.

6 -4 Electrode Potentials for Nonstandard C o n d i t i o n s The Nernst Equation The Application of Nernst Equation

• The Nernst Equation The Nernst equation can be used to calculate E values at other conditions. For a reduction half-reaction Oxidation state + n e reduction state

This is famous Nernst equation, where: φ is the electrode potential at nonstandard condition; R is the gas constant, R=8. 314 J/(mol·K) ; T is the absolute temperature; n is the number of electrons transferred between the species; F is the Faraday constant, equal to 96500 C/mol; [ox], [red] represent concentration respectively.

The Nernst equation for the φ of a half-cell at 25℃ is Notice that in the expression for Nernst equation ─

• reducing species (right side of a half reaction) appear in the denominator. • oxidizing species (left side of a half reaction) appear in the numerator. • each concentration or partial pressure of a substance is raised to a power equal to its coefficient in the half reaction. • Pure liquids and solids do not appear in the Nernst equation. • H+ or OH- enter Nernst equation.

Br 2 (l) + 2 e Cr 2 O 72 - +14 H++6 e 2 Br - 2 Cr 3+ +7 H 2 O

• The Application of Nernst Equation 1. Calculate the electrode potential Example 6 -1 Calculate the electrode potential of following electrode in p. H =5 solution ? Pt|Mn. O 4 - (1. 0), Mn 2+(1. 0), H+ (10 -5) Solution: Electrode half-reaction is Mn. O 4 - +8 H+ +5 e → Mn 2+ + 4 H 2 O
![n5 O Mn O4H8 1 036 v n=5 O [Mn. O-4][H+]8 =1. 036 (v)](https://slidetodoc.com/presentation_image/464b25d950fc24be7e64a833e726c4db/image-44.jpg)
n=5 O [Mn. O-4][H+]8 =1. 036 (v)

Example 6 -2 Calculate φ for the half-reaction Sn 4+ + 2 e- Sn 2+ At 25 ℃ if the concentration of Sn 2+ is 0. 40 mol/L and the concentration of Sn 4+ is 0. 10 mol/L. Solution:

2. Calculate the cell emf (E) Example 6 -3 The copper-zinc cell shown below. If the reaction is done in a cell in 5. 00 mol/L Zn 2+ and 0. 30 mol/L Cu 2+ at 25℃, Zn(s) + Cu 2+(a q) → Cu(s) + Zn 2+(a q) (a) write the cell formulation (notation) (b) what is the cell E ? Solution: Anode: Zn 2+ + 2 e → Zn(s) φ° = - 0. 76 V Cathode: Cu 2+ + 2 e → Cu(s) φ° = 0. 34 V

According to the Nernst equation

Cu electrode is cathode; Zn electrode is anode. (a) The cell formulation (notation) is: (-) Zn(s)│Zn 2+(aq) Cu 2+(aq)│Cu (s) (+) (b) E= φ+-φ-=0. 3245 -(-0. 7393)=1. 0638 V

Example Applying the Nernst equation for determining E. (a) What is the value of the cell E for the diagrammed bellow ? (b) write out the cell reaction and electrode reaction. Pt│Fe 3+(0. 05), Fe 2+(0. 5 q) Ce 4+(1)│Ce 3+(0. 01) │Pt Solution: (a) On the right half-reaction: Ce 4+ + e Ce 3+

On the left half-reaction: Fe 3+ + e Fe 2+

Ce 4+/Ce 3+ is positive electrode Fe 3+/Fe 2+ is negative electrode E = φ+ - φ- =1. 73 -0. 712=1. 018(V) (b) Cathode: Ce 4+ + e →Ce 3+ Anode: Fe 2+ - e →Fe 3+ Cell reaction: Ce 4+ + Fe 2+ →Ce 3+ + Fe 3+

3. Use of the Nernst Equation to Calculate Ion Concentrations Example 6 -4 If the voltage of the cell bellow is 0. 389 V in a 0. 500 mol/L solution of Fe 2+ , 1 atm pressure of H 2 at 25 ℃ , what is the hydrogen concentration in the solution ? Fe│Fe 2+ H+│H 2 │Pt Solution: Fe 2+ + 2 e → Fe φ° = - 0. 41 V 2 H+ + 2 e → H 2 φ° = 0. 00 V

![E φφ 0 0592 logH0 4189 0 389 V H0 3125 molL E= φ+-φ-= 0. 0592 log[H+]-(-0. 4189) = 0. 389 V [H+]=0. 3125 mol/L](https://slidetodoc.com/presentation_image/464b25d950fc24be7e64a833e726c4db/image-54.jpg)
E= φ+-φ-= 0. 0592 log[H+]-(-0. 4189) = 0. 389 V [H+]=0. 3125 mol/L

4. Predicting Spontaneous Reactions for Nonstandard Conditions. n Decide the following reaction weather is a spontaneous process: Pb 2+ (c=0. 01) + Sn = Pb + 2+ Sn Solution: (c=1. 0)
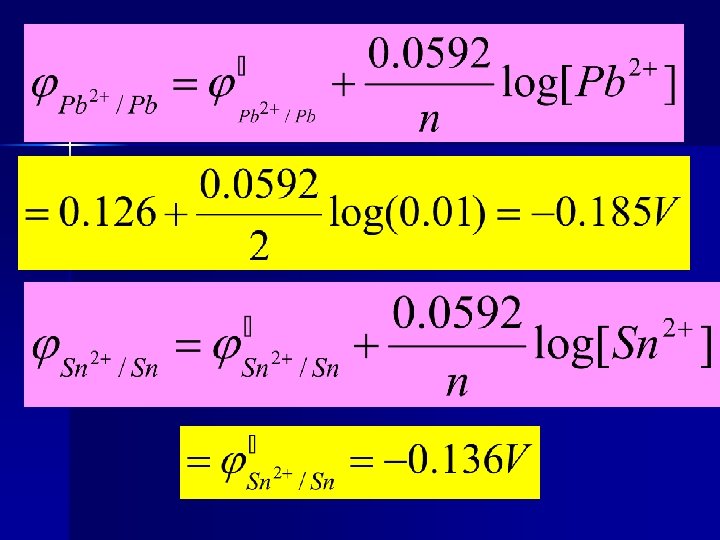

2+ Sn + Pb = 2+ Pb + Sn

Will the redox reaction proceed spontaneously as written for the following reaction ? Fe 2+(0. 015) + Ag+(0. 25) →Fe 3+(0. 35)+Ag(s) Answer: The reaction is nonspontaneous as written.

Practice: Calculate E for the following voltaic cell. Ag(s)│Ag+(1. 0) Hg 2+(0. 001) , Hg(l) │Pt (a) What is the value of the cell E for the diagrammed bellow ? (b) write out the cell reaction and electrode reaction.

6 -5 Determination of p. H Reference electrode cell e. g. , SCE electrode, SHE Ag-Ag. Cl electrode Indicator electrode e. g. , hydrogen electrode p. H glass electrode

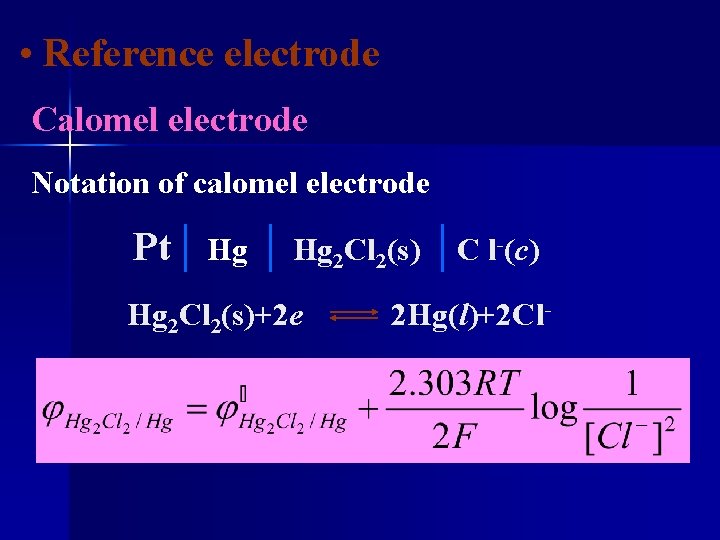
• Reference electrode Calomel electrode Notation of calomel electrode Pt│ Hg 2 Cl 2(s) │C l-(c) Hg 2 Cl 2(s)+2 e 2 Hg(l)+2 Cl-

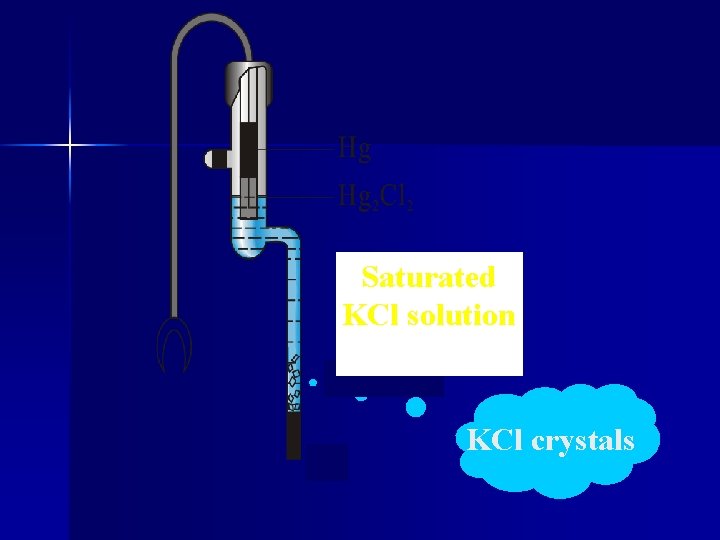
T=298 K, Saturated calomel electrode

Saturated KCl solution KCl crystals

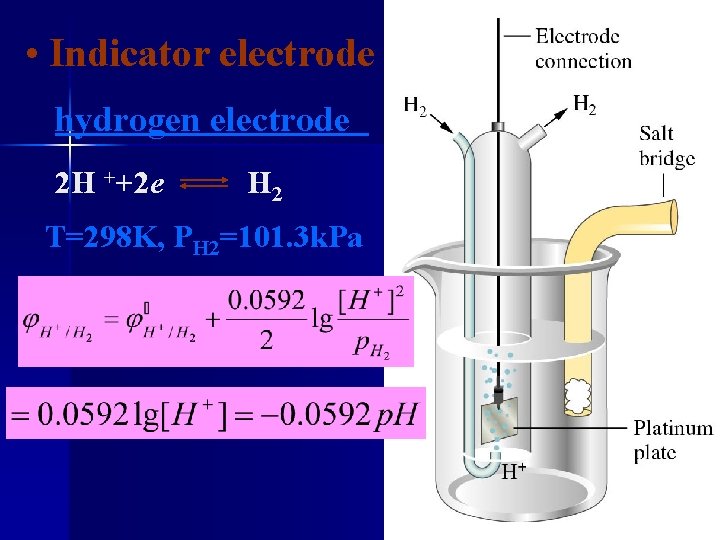
• Indicator electrode hydrogen electrode 2 H ++2 e H 2 T=298 K, PH 2=101. 3 k. Pa

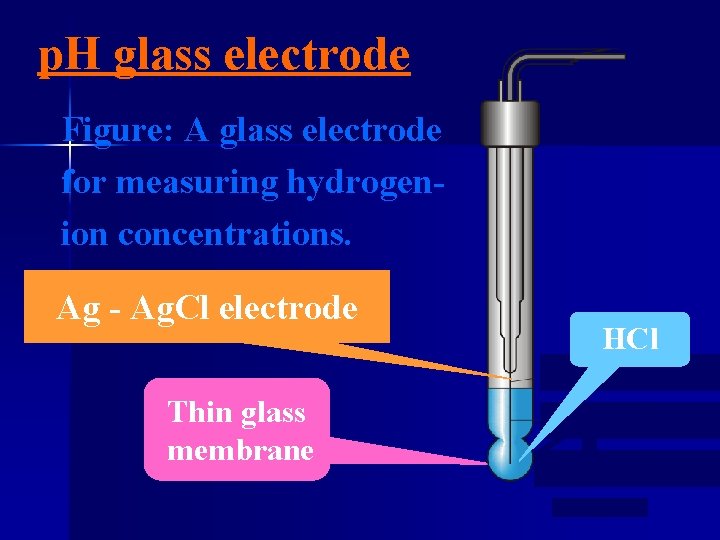
p. H glass electrode Figure: A glass electrode for measuring hydrogenion concentrations. Ag - Ag. Cl electrode Thin glass membrane HCl

Notation of glass electrode Ag , Ag. Cl(s) |H +(1 M) | glass membrane | measured solution glass electrode | measured solution (p. Hx ) ΦG=φ°G + 0. 0592 log[H+] =φ°G - 0. 0592 p. H

• Measurement p. H value of a solution by hydrogen electrode Cell notation (-) Pt|H 2(1 atm) | H+ (p. H x) | | SCE (+) 25℃ Φ+= φ SCE = + 0. 2412 V E= Φ+-Φ-= 0. 2412+0. 0592 p. H

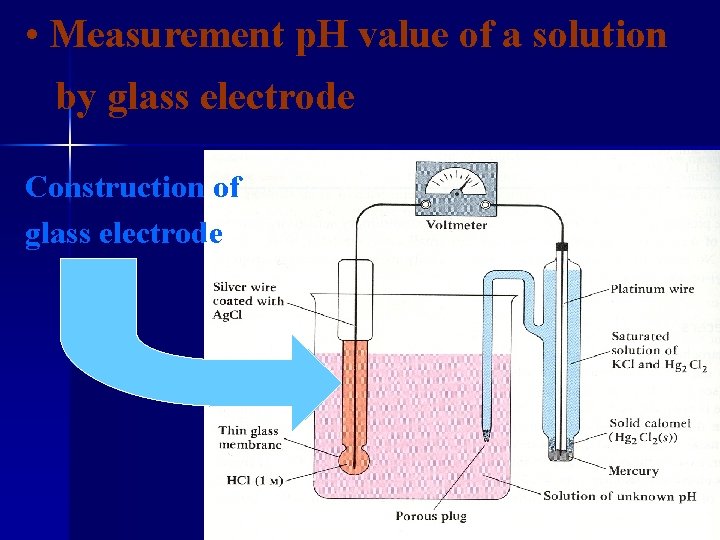
• Measurement p. H value of a solution by glass electrode Construction of glass electrode

First step (-) glass electrode | p. Hs standard buffer| | SCE (+) (1)

Second step (-) glass electrode | p. H x solution| | SCE (+) (2) (1)
