6 3 Angles Radian Measure OBJECTIVES 1 USE

6. 3 Angles & Radian Measure OBJECTIVES: 1. USE A ROTATING RAY TO EXTEND THE DEFINITION OF ANGLE MEASURE TO NEGATIVE ANGLES AND ANGLES GREATER THAN 180°. 2. DEFINE RADIAN MEASURE AND CONVERT ANGLE MEASURES BETWEEN DEGREES AND RADIANS.

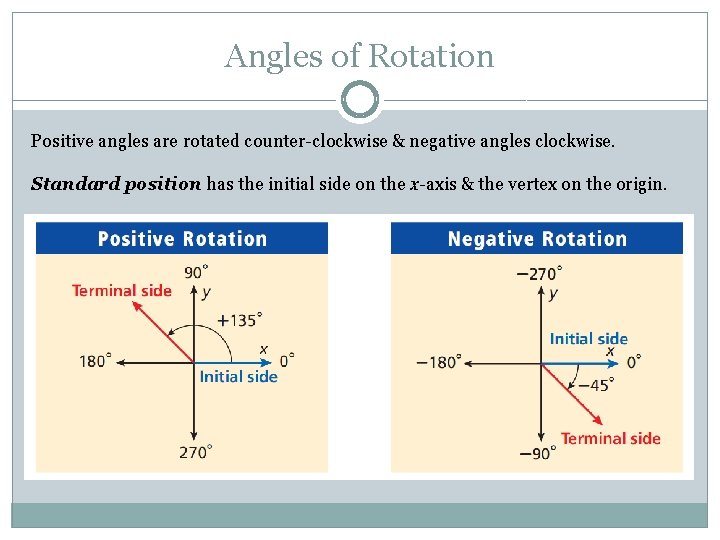
Angles of Rotation Positive angles are rotated counter-clockwise & negative angles clockwise. Standard position has the initial side on the x-axis & the vertex on the origin.

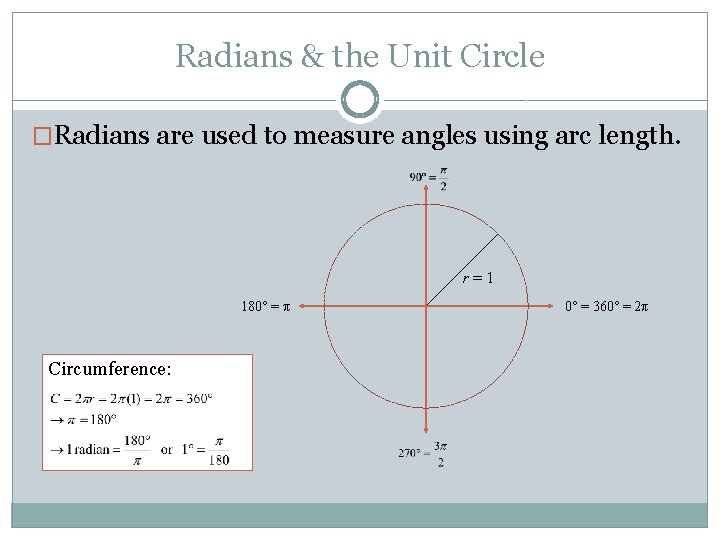
Radians & the Unit Circle �Radians are used to measure angles using arc length. r=1 180° = π Circumference: 0° = 360° = 2π

Example #1 Convert from Radians to Degrees A. B. C.

Example #2 Convert from Degrees to Radians A. 150° B. -330° C. 540°

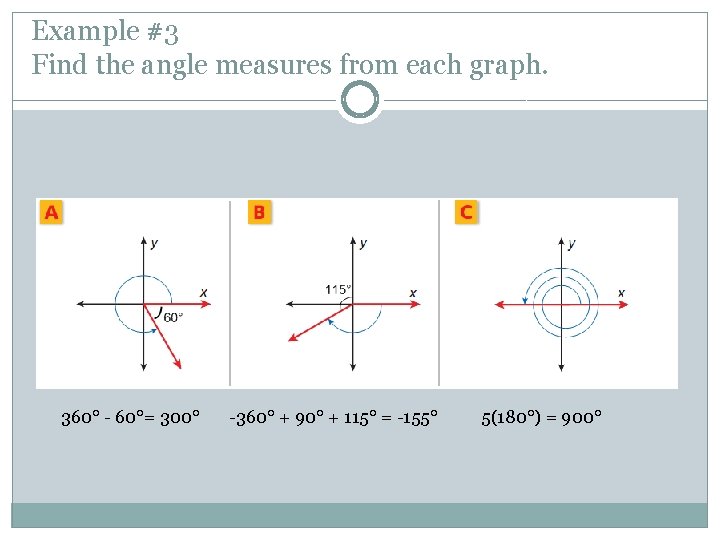
Example #3 Find the angle measures from each graph. 360° - 60°= 300° -360° + 90° + 115° = -155° 5(180°) = 900°

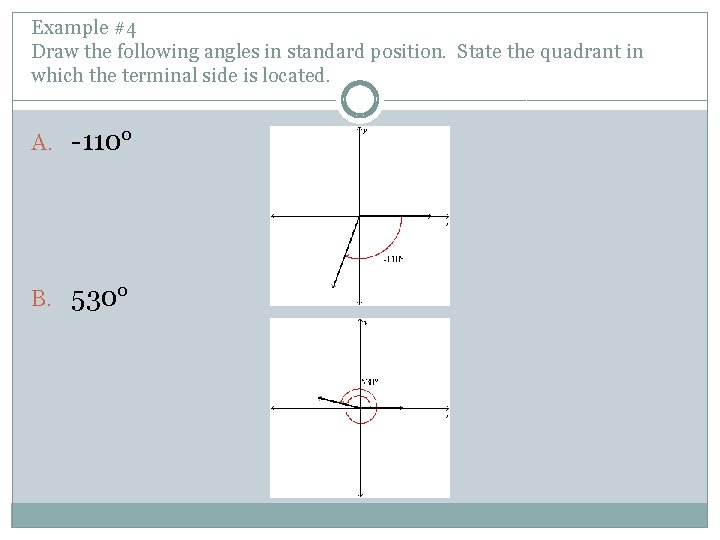
Example #4 Draw the following angles in standard position. State the quadrant in which the terminal side is located. A. -110° B. 530°

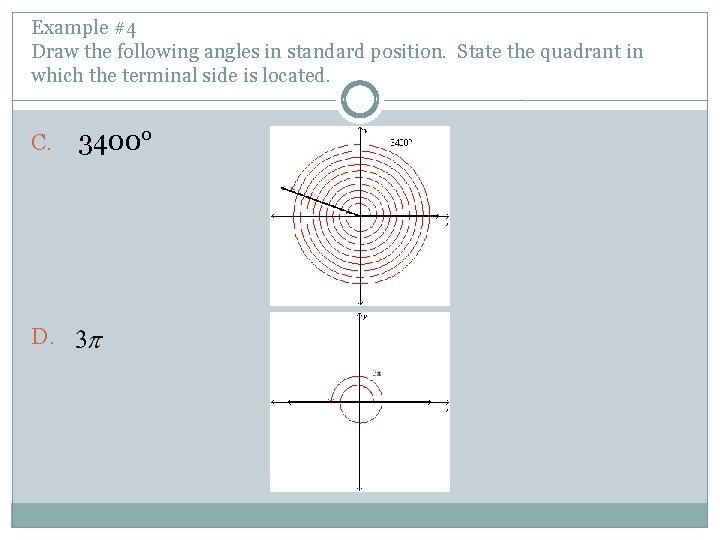
Example #4 Draw the following angles in standard position. State the quadrant in which the terminal side is located. C. D. 3400°

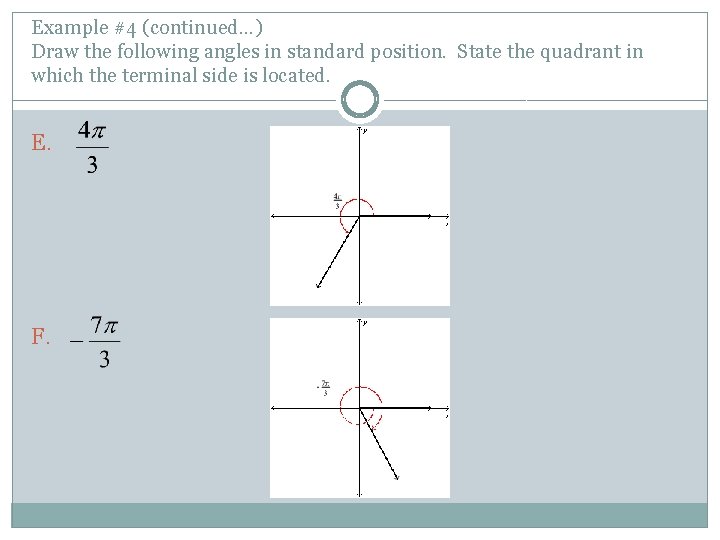
Example #4 (continued…) Draw the following angles in standard position. State the quadrant in which the terminal side is located. E. F.

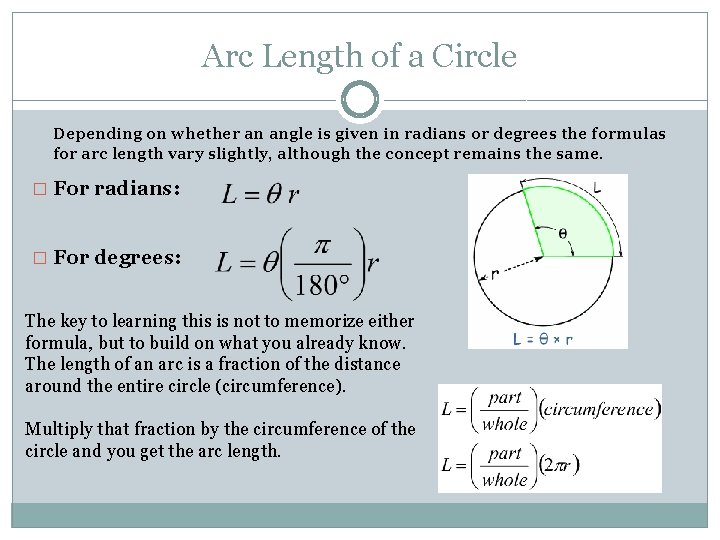
Arc Length of a Circle Depending on whether an angle is given in radians or degrees the formulas for arc length vary slightly, although the concept remains the same. � For radians: � For degrees: The key to learning this is not to memorize either formula, but to build on what you already know. The length of an arc is a fraction of the distance around the entire circle (circumference). Multiply that fraction by the circumference of the circle and you get the arc length.

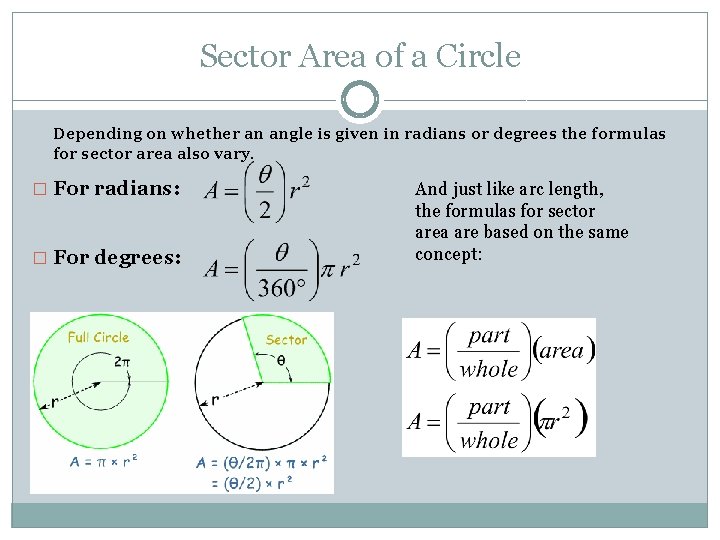
Sector Area of a Circle Depending on whether an angle is given in radians or degrees the formulas for sector area also vary. � For radians: � For degrees: And just like arc length, the formulas for sector area are based on the same concept:

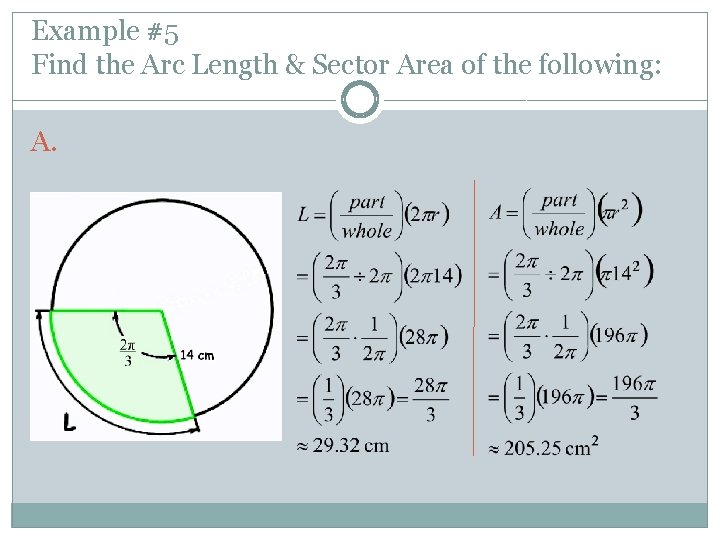
Example #5 Find the Arc Length & Sector Area of the following: A.

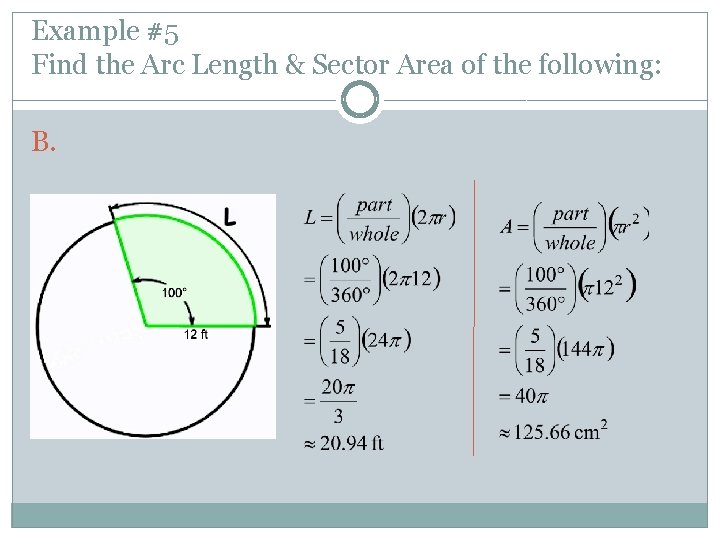
Example #5 Find the Arc Length & Sector Area of the following: B.

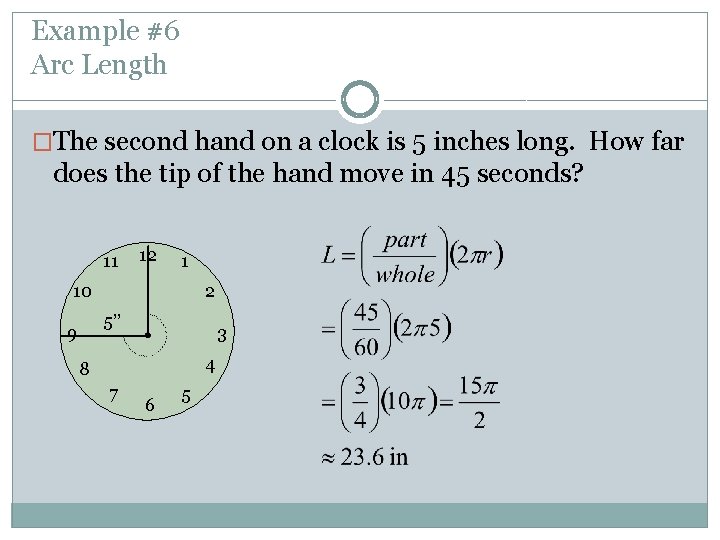
Example #6 Arc Length �The second hand on a clock is 5 inches long. How far does the tip of the hand move in 45 seconds? 11 12 1 10 2 5’’ 9 3 4 8 7 6 5