6 2 Differential Equations Growth and Decay Part

6. 2 Differential Equations: Growth and Decay (Part 1) Glacier National Park, Montana Photo by Vickie Kelly, 2004 Greg Kelly, Hanford High School, Richland, Washington

Objectives • Use separation of variables to solve a simple differential equation. • Use exponential functions to model growth and decay in applied problems.

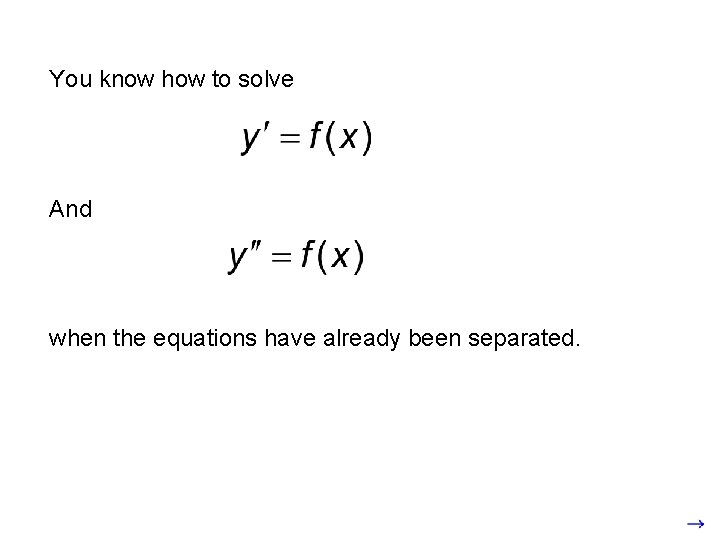
You know how to solve And when the equations have already been separated.

Solve the differential equation Solution set of all equations where

The number of bighorn sheep in a population increases at a rate that is proportional to the number of sheep present (at least for awhile. ) So does any population of living creatures. Other things that increase or decrease at a rate proportional to the amount present include radioactive material and money in an interest-bearing account. If the rate of change is proportional to the amount present, the change can be modeled by:

Growth and Decay Models: Rate of change is proportional to the amount present. Divide both sides by y. Integrate both sides.

Integrate both sides. Exponentiate both sides. When multiplying like bases, add exponents. So added exponents can be written as multiplication.

Exponentiate both sides. When multiplying like bases, add exponents. So added exponents can be written as multiplication. Since is a constant, let .

Since At is a constant, let , . This is the solution to our original initial value problem. .

Theorem 5. 16: Exponential Growth and Decay If y is a differentiable function of t such that y>0 and y'=ky for some constant k, then Exponential Change: If the constant k is positive then the equation represents growth. If k is negative then the equation represents decay.

Example: The rate of change of y is proportional to y. When t=0, y=2. When t=2, y=4. What is the value of y when t=3?

Homework 6. 2 (page 420) #1 -25 odd