6 1 Simple Trusses 1 Definition of Truss

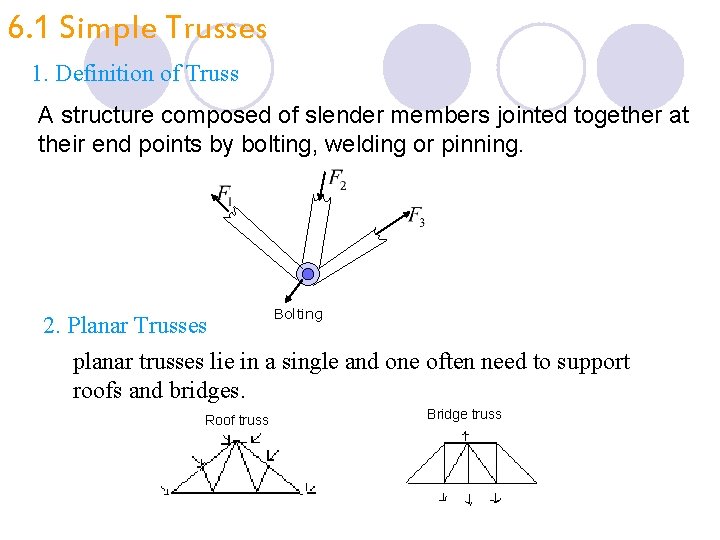
6. 1 Simple Trusses 1. Definition of Truss A structure composed of slender members jointed together at their end points by bolting, welding or pinning. 2. Planar Trusses Bolting planar trusses lie in a single and one often need to support roofs and bridges. Roof truss Bridge truss

3. Assumption for Truss (1) all loading are applied at the joints a. members’ weights are neglected (W << external force) b. members’ weights are included (2) members are jointed together by smooth pin (No friction forces) Because of the two assumptions, the truss member is a two-force member T T Tensile force T C Compression force Note: Compression member must be made thicken than tension member because of the buckling or column effect in compression member.

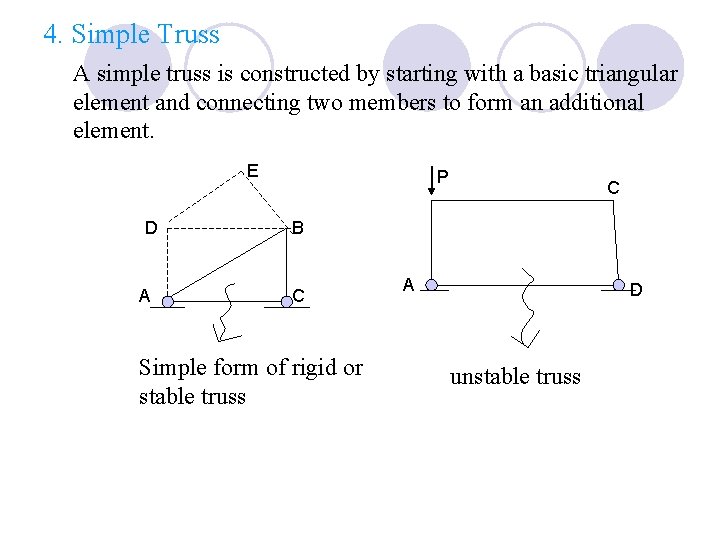
4. Simple Truss A simple truss is constructed by starting with a basic triangular element and connecting two members to form an additional element. E D A P C B C Simple form of rigid or stable truss A D unstable truss

6. 2 the Method of Joints 1. Objective Evaluate the force acting on each member of a truss structure to analyze or design a truss 2. Concept A truss is in equilibrium, so each of its joint also is in equilibrium Force system acting at pin or joint is coplanar and concurrent Therefore, we have (A)member equilibrium is automatically satisfied at each joint (B)Only force equilibrium ΣFx=0 and ΣFy=0 is necessary

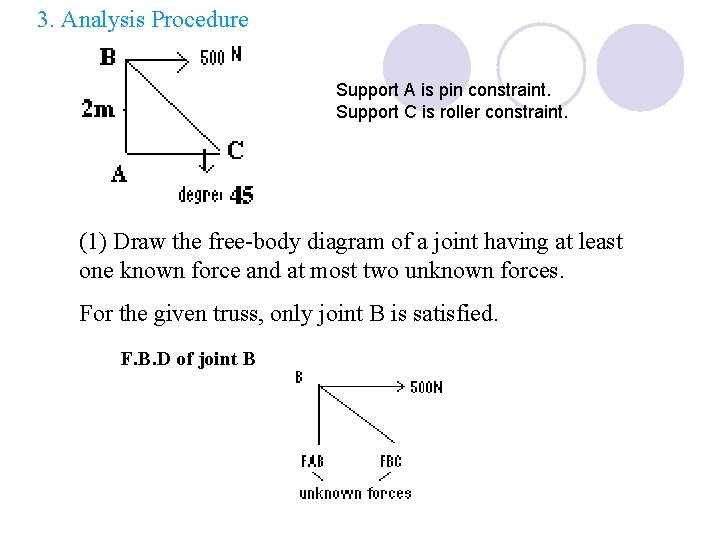
3. Analysis Procedure Support A is pin constraint. Support C is roller constraint. (1) Draw the free-body diagram of a joint having at least one known force and at most two unknown forces. For the given truss, only joint B is satisfied. F. B. D of joint B

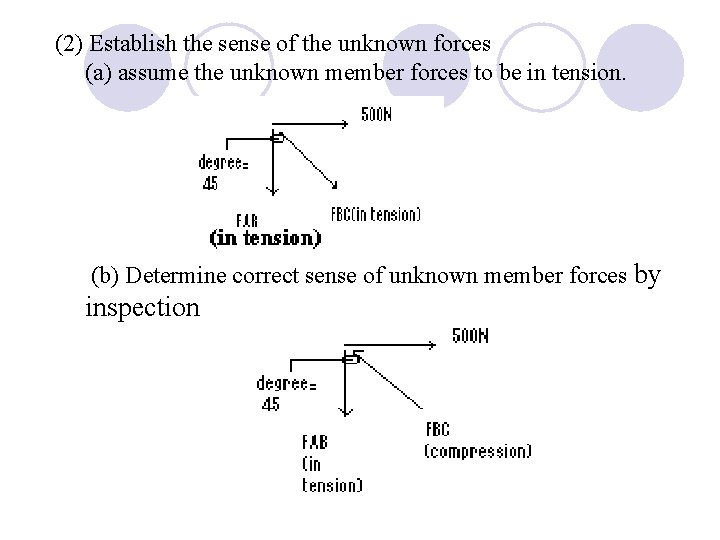
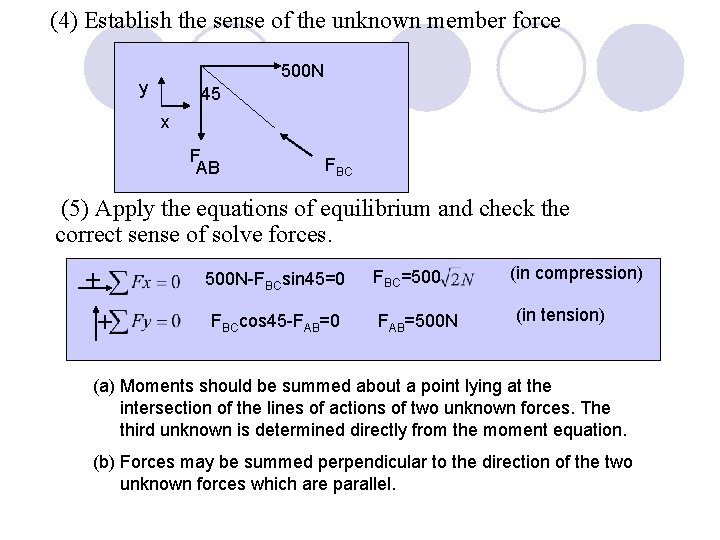
(2) Establish the sense of the unknown forces (a) assume the unknown member forces to be in tension. (b) Determine correct sense of unknown member forces by inspection

(3) Apply the force equilibrium equations ΣFx=0 500+FBC sin 45°=0 ΣFy=0 -FAB-FBCcos 45°=0 (4) Solve the unknown forces and check their correct sense FBC=- 500/sin 45°=-500√ 2 N (in compression) FAB=-FBCcos 45°=500 N (in tension) (5) Continue to analyze then joints by repeating steps (1) to (4)

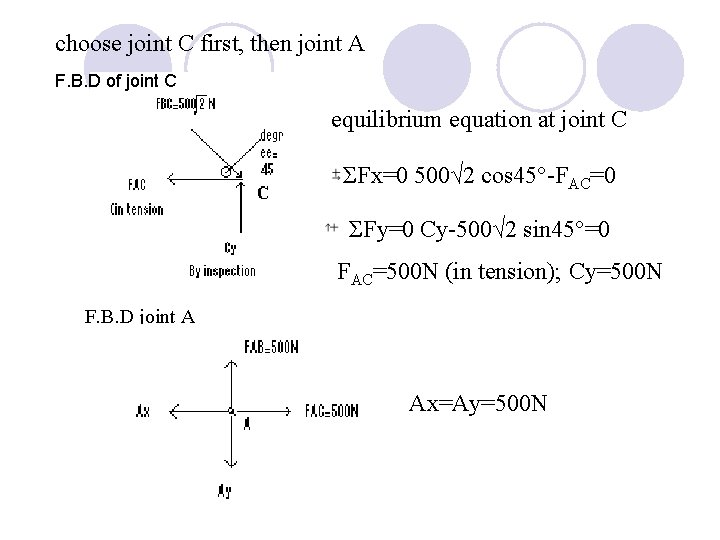
choose joint C first, then joint A F. B. D of joint C equilibrium equation at joint C ΣFx=0 500√ 2 cos 45°-FAC=0 ΣFy=0 Cy-500√ 2 sin 45°=0 FAC=500 N (in tension); Cy=500 N F. B. D joint A Ax=Ay=500 N

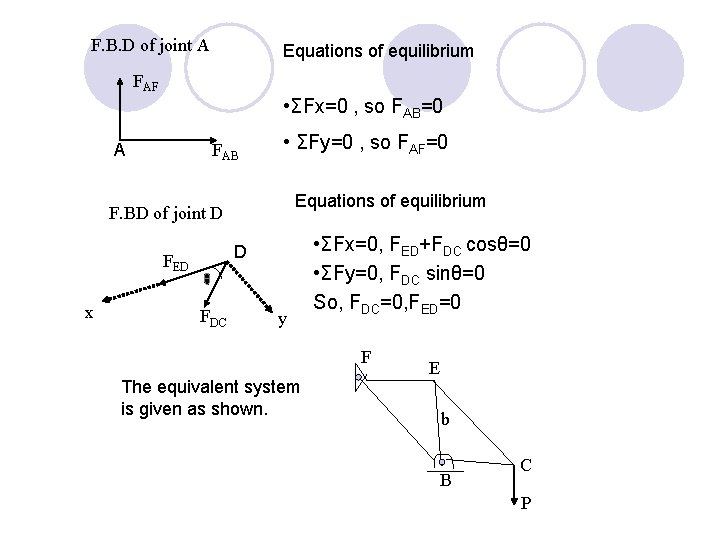
6 -3 zero-force members 1. zero-force member A member supports no loading, which is used to increase the stability of the truss and to provide support if the applied loading is changed. 2. Rules for determining zero-force members (1) If only two members form a truss joint and no external load or support reaction is applied to the joint. Ex. F A D E C B Joint A and joint D are formed by two members AF &AB, ED&CD respectively and no loading is applied. Hence, members AF, A, ED and CD are zero-force members.

F. B. D of joint A Equations of equilibrium FAF • ΣFx=0 , so FAB=0 A FAB • ΣFy=0 , so FAF=0 Equations of equilibrium F. BD of joint D D FED x FDC y • ΣFx=0, FED+FDC cosθ=0 • ΣFy=0, FDC sinθ=0 So, FDC=0, FED=0 F The equivalent system is given as shown. E b B C P

(2) If three members form a truss joint for which two of the members are collinear , the third member is zero-force members provided no external force or support reaction is applied to the joint. EX: P E D A C B Joint D : 3 members AD, ED and CD (ED &DC collinear) Joint C : 3 members AD, DC and CB (DC& CB collinear) No external force or support reaction is applied to the joint D & C. ∴AD and AC zero-force members

6 -4 The method of section 1. Purpose Determine the loadings acting within a body. 2. Principle If a body is equilibrium , then any part of the body is also in equilibrium. T T In equilibrium F F Imaginary section F=T Internal tension force In equilibrium T F=T Apply the equations of equilibrium to the sectioned part to determine the loading at the section.

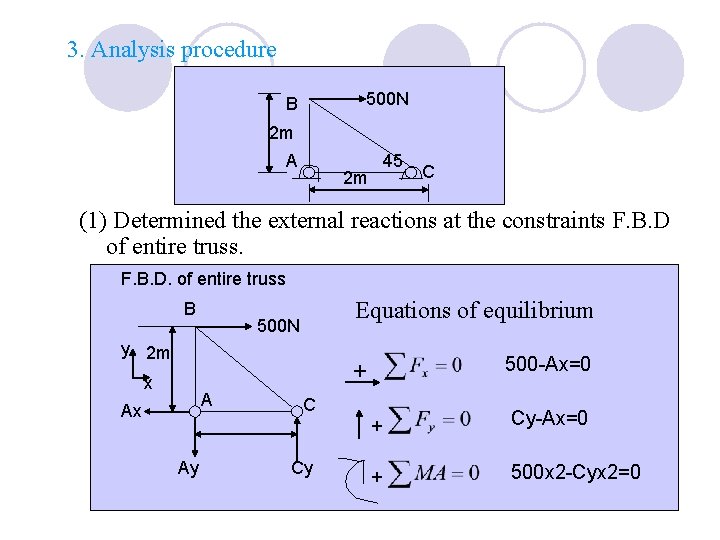
3. Analysis procedure 500 N B 2 m A 45 2 m C (1) Determined the external reactions at the constraints F. B. D of entire truss. F. B. D. of entire truss B Equations of equilibrium 500 N y 2 m 500 -Ax=0 + x A Ax Ay C Cy + Cy-Ax=0 + 500 x 2 -Cyx 2=0

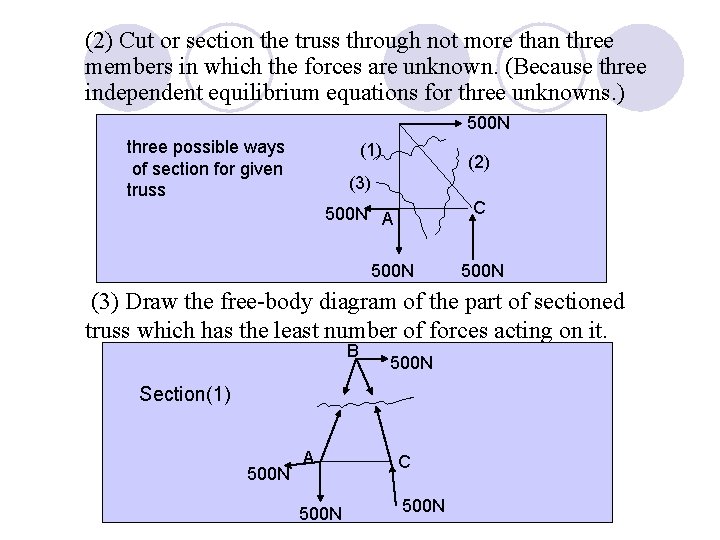
(2) Cut or section the truss through not more than three members in which the forces are unknown. (Because three independent equilibrium equations for three unknowns. ) 500 N three possible ways of section for given truss (1) (2) (3) C 500 N A 500 N (3) Draw the free-body diagram of the part of sectioned truss which has the least number of forces acting on it. B 500 N Section(1) 500 N A C 500 N

(4) Establish the sense of the unknown member force 500 N y 45 x F AB FBC (5) Apply the equations of equilibrium and check the correct sense of solve forces. + + 500 N-FBCsin 45=0 FBCcos 45 -FAB=0 FBC=500 FAB=500 N (in compression) (in tension) (a) Moments should be summed about a point lying at the intersection of the lines of actions of two unknown forces. The third unknown is determined directly from the moment equation. (b) Forces may be summed perpendicular to the direction of the two unknown forces which are parallel.

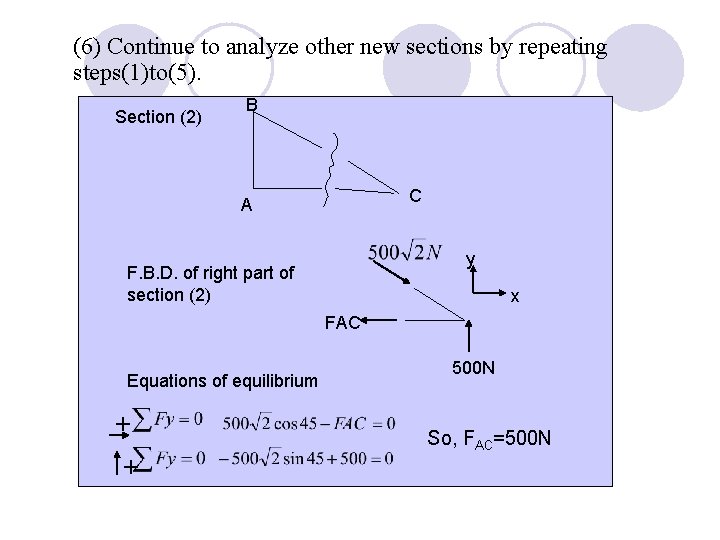
(6) Continue to analyze other new sections by repeating steps(1)to(5). Section (2) B C A y F. B. D. of right part of section (2) x FAC Equations of equilibrium + + 500 N So, FAC=500 N

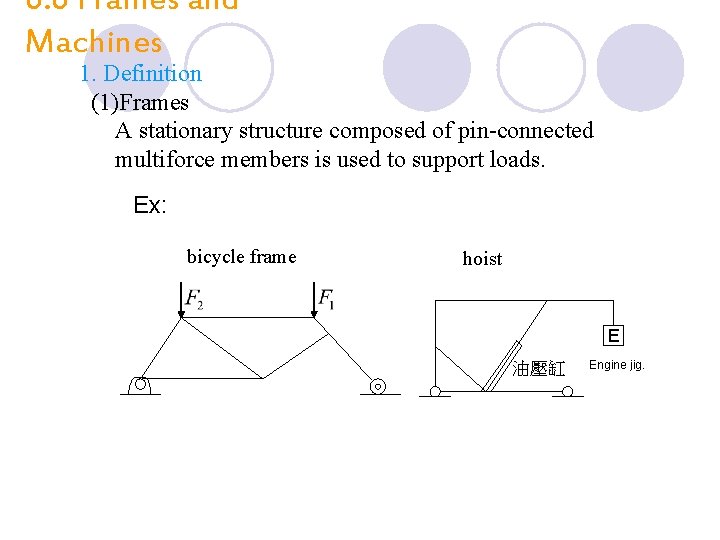
6. 6 Frames and Machines 1. Definition (1)Frames A stationary structure composed of pin-connected multiforce members is used to support loads. Ex: bicycle frame hoist E 油壓缸 Engine jig.

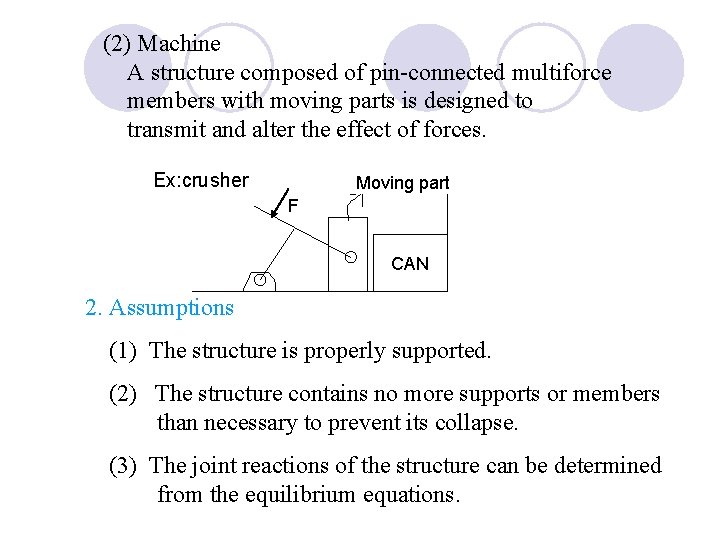
(2) Machine A structure composed of pin-connected multiforce members with moving parts is designed to transmit and alter the effect of forces. Ex: crusher Moving part F CAN 2. Assumptions (1) The structure is properly supported. (2) The structure contains no more supports or members than necessary to prevent its collapse. (3) The joint reactions of the structure can be determined from the equilibrium equations.

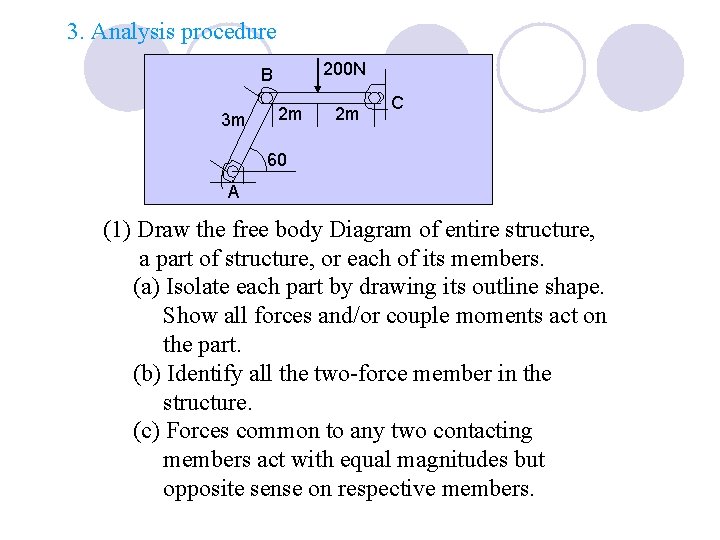
3. Analysis procedure 200 N B 3 m 2 m 2 m C 60 A (1) Draw the free body Diagram of entire structure, a part of structure, or each of its members. (a) Isolate each part by drawing its outline shape. Show all forces and/or couple moments act on the part. (b) Identify all the two-force member in the structure. (c) Forces common to any two contacting members act with equal magnitudes but opposite sense on respective members.

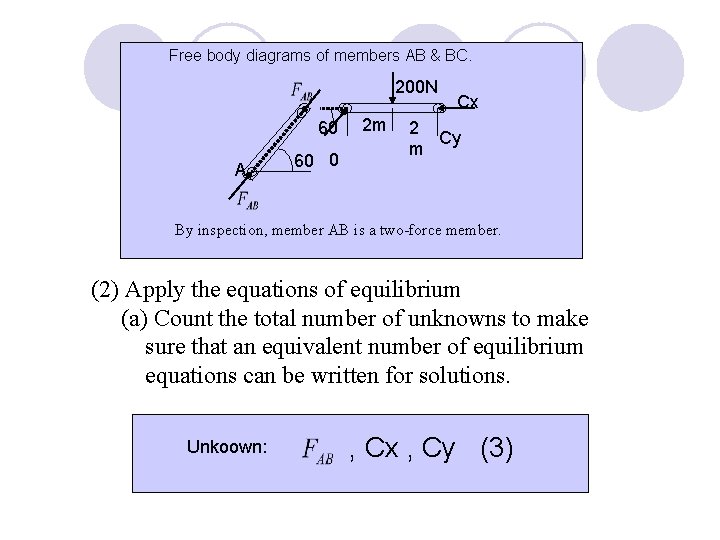
Free body diagrams of members AB & BC. 200 N 60 A 60 0 2 m Cx 2 Cy m By inspection, member AB is a two-force member. (2) Apply the equations of equilibrium (a) Count the total number of unknowns to make sure that an equivalent number of equilibrium equations can be written for solutions. Unkoown: , Cx , Cy (3)

(b) Moments should be summed about a point that lies at the intersection of the lines of action of as many unknown forces as possible. Equations of equilibrium for member BC. (2) Check the correct sense of the unknown forces.