6 1 Properties and Attributes of Polygons Objectives

6 -1 Properties and Attributes of Polygons Objectives Classify polygons based on their sides and angles. Find and use the measures of interior and exterior angles of polygons. Holt Geometry

6 -1 Properties and Attributes of Polygons Vocabulary side of a polygon vertex of a polygon diagonal regular polygon concave convex Holt Geometry

6 -1 Properties and Attributes of Polygons Each segment that forms a polygon is a side of the polygon. The common endpoint of two sides is a vertex of the polygon. A segment that connects any two nonconsecutive vertices is a diagonal. Holt Geometry

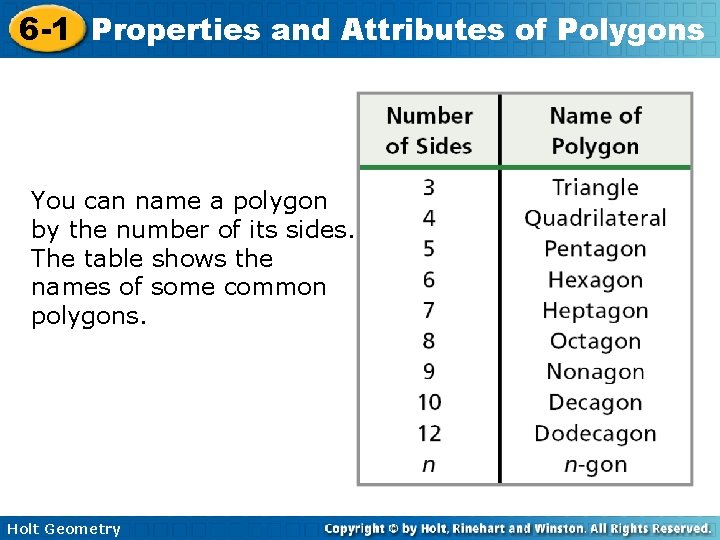
6 -1 Properties and Attributes of Polygons You can name a polygon by the number of its sides. The table shows the names of some common polygons. Holt Geometry

6 -1 Properties and Attributes of Polygons Example 1 A: Identifying Polygons Tell whether the figure is a polygon. If it is a polygon, name it by the number of sides. polygon, hexagon Holt Geometry

6 -1 Properties and Attributes of Polygons Example 1 B: Identifying Polygons Tell whether the figure is a polygon. If it is a polygon, name it by the number of sides. polygon, heptagon Holt Geometry

6 -1 Properties and Attributes of Polygons Example 1 C: Identifying Polygons Tell whether the figure is a polygon. If it is a polygon, name it by the number of sides. not a polygon Holt Geometry

6 -1 Properties and Attributes of Polygons Check It Out! Example 1 a Tell whether each figure is a polygon. If it is a polygon, name it by the number of its sides. not a polygon Holt Geometry

6 -1 Properties and Attributes of Polygons Check It Out! Example 1 b Tell whether the figure is a polygon. If it is a polygon, name it by the number of its sides. polygon, nonagon Holt Geometry

6 -1 Properties and Attributes of Polygons Check It Out! Example 1 c Tell whether the figure is a polygon. If it is a polygon, name it by the number of its sides. not a polygon Holt Geometry

6 -1 Properties and Attributes of Polygons All the sides are congruent in an equilateral polygon. All the angles are congruent in an equiangular polygon. A regular polygon is one that is both equilateral and equiangular. If a polygon is not regular, it is called irregular. Holt Geometry

6 -1 Properties and Attributes of Polygons A polygon is concave if any part of a diagonal contains points in the exterior of the polygon. If no diagonal contains points in the exterior, then the polygon is convex. A regular polygon is always convex. Holt Geometry

6 -1 Properties and Attributes of Polygons Example 2 A: Classifying Polygons Tell whether the polygon is regular or irregular. Tell whether it is concave or convex. irregular, convex Holt Geometry

6 -1 Properties and Attributes of Polygons Example 2 B: Classifying Polygons Tell whether the polygon is regular or irregular. Tell whether it is concave or convex. irregular, concave Holt Geometry

6 -1 Properties and Attributes of Polygons Example 2 C: Classifying Polygons Tell whether the polygon is regular or irregular. Tell whether it is concave or convex. regular, convex Holt Geometry

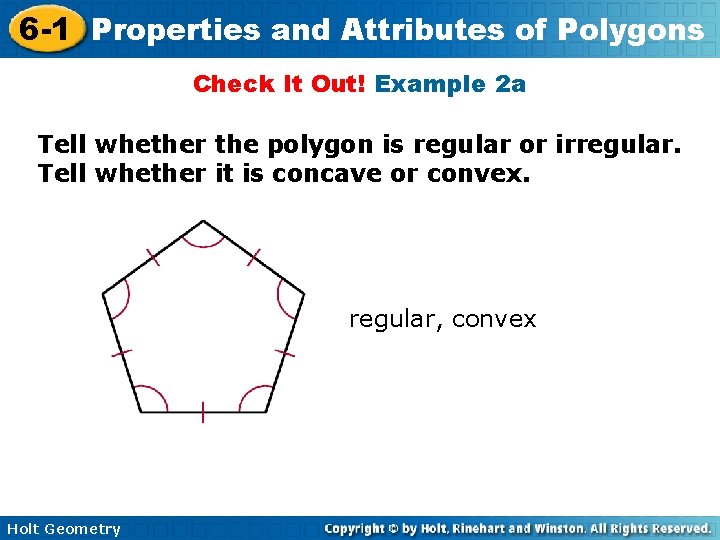
6 -1 Properties and Attributes of Polygons Check It Out! Example 2 a Tell whether the polygon is regular or irregular. Tell whether it is concave or convex. regular, convex Holt Geometry

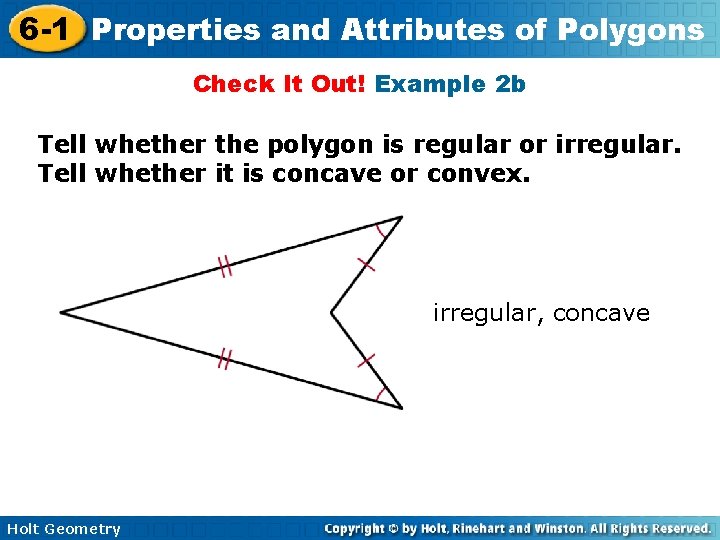
6 -1 Properties and Attributes of Polygons Check It Out! Example 2 b Tell whether the polygon is regular or irregular. Tell whether it is concave or convex. irregular, concave Holt Geometry

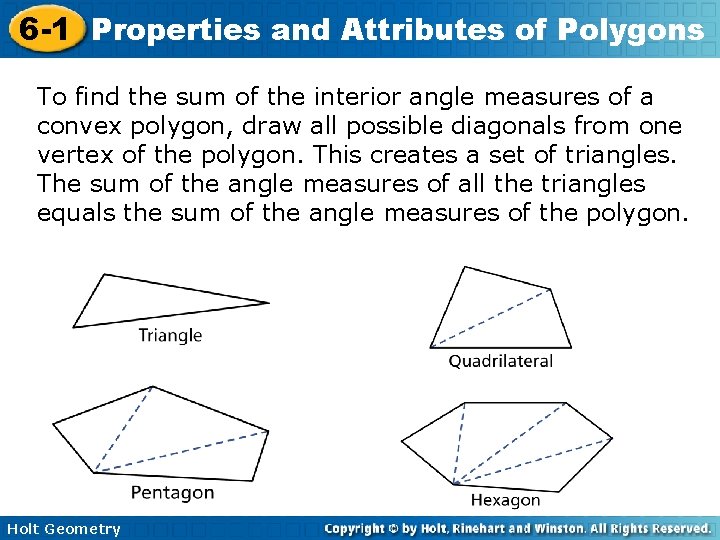
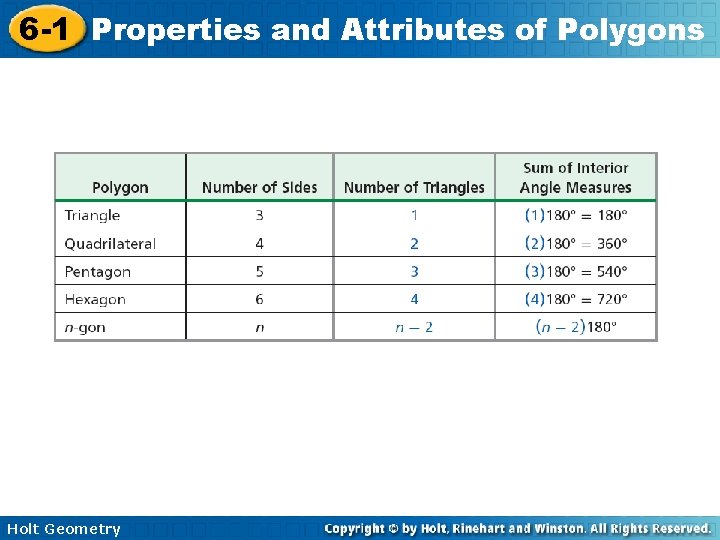
6 -1 Properties and Attributes of Polygons To find the sum of the interior angle measures of a convex polygon, draw all possible diagonals from one vertex of the polygon. This creates a set of triangles. The sum of the angle measures of all the triangles equals the sum of the angle measures of the polygon. Holt Geometry

6 -1 Properties and Attributes of Polygons Remember! By the Triangle Sum Theorem, the sum of the interior angle measures of a triangle is 180°. Holt Geometry

6 -1 Properties and Attributes of Polygons Holt Geometry

6 -1 Properties and Attributes of Polygons In each convex polygon, the number of triangles formed is two less than the number of sides n. So the sum of the angle measures of all these triangles is (n — 2)180°. Holt Geometry

6 -1 Properties and Attributes of Polygons Example 3 A: Finding Interior Angle Measures and Sums in Polygons Find the sum of the interior angle measures of a convex heptagon. (n – 2)180° Polygon Sum Thm. (7 – 2)180° A heptagon has 7 sides, so substitute 7 for n. 900° Holt Geometry Simplify.

6 -1 Properties and Attributes of Polygons Check It Out! Example 3 a Find the sum of the interior angle measures of a convex 15 -gon. (n – 2)180° Polygon Sum Thm. (15 – 2)180° A 15 -gon has 15 sides, so substitute 15 for n. 2340° Holt Geometry Simplify.

6 -1 Properties and Attributes of Polygons Example 3 B: Finding Interior Angle Measures and Sums in Polygons Find the measure of each interior angle of a regular 16 -gon. Step 1 Find the sum of the interior angle measures. (n – 2)180° Polygon Sum Thm. (16 – 2)180° = 2520° Substitute 16 for n and simplify. Step 2 Find the measure of one interior angle. The int. s are , so divide by 16. Holt Geometry

6 -1 Properties and Attributes of Polygons Check It Out! Example 3 b Find the measure of each interior angle of a regular decagon. Step 1 Find the sum of the interior angle measures. (n – 2)180° Polygon Sum Thm. (10 – 2)180° = 1440° Substitute 10 for n and simplify. Step 2 Find the measure of one interior angle. The int. s are , so divide by 10. Holt Geometry

6 -1 Properties and Attributes of Polygons Example 3 C: Finding Interior Angle Measures and Sums in Polygons Find the measure of each interior angle of pentagon ABCDE. (5 – 2)180° = 540° Polygon Sum Thm. Polygon m A + m B + m C + m D + m E = 540° Sum Thm. 35 c + 18 c + 32 c + 18 c = 540 135 c = 540 c=4 Holt Geometry Substitute. Combine like terms. Divide both sides by 135.

6 -1 Properties and Attributes of Polygons Example 3 C Continued m A = 35(4°) = 140° m B = m E = 18(4°) = 72° m C = m D = 32(4°) = 128° Holt Geometry

6 -1 Properties and Attributes of Polygons In the polygons below, an exterior angle has been measured at each vertex. Notice that in each case, the sum of the exterior angle measures is 360°. Holt Geometry

6 -1 Properties and Attributes of Polygons Holt Geometry

6 -1 Properties and Attributes of Polygons Example 4 A: Finding Interior Angle Measures and Sums in Polygons Find the measure of each exterior angle of a regular 20 -gon. A 20 -gon has 20 sides and 20 vertices. sum of ext. s = 360°. measure of one ext. = Polygon Sum Thm. A regular 20 -gon has 20 ext. s, so divide the sum by 20. The measure of each exterior angle of a regular 20 -gon is 18°. Holt Geometry

6 -1 Properties and Attributes of Polygons Check It Out! Example 4 a Find the measure of each exterior angle of a regular dodecagon. A dodecagon has 12 sides and 12 vertices. sum of ext. s = 360°. measure of one ext. Polygon Sum Thm. A regular dodecagon has 12 ext. s, so divide the sum by 12. The measure of each exterior angle of a regular dodecagon is 30°. Holt Geometry

6 -1 Properties and Attributes of Polygons Example 4 B: Finding Interior Angle Measures and Sums in Polygons Find the value of b in polygon FGHJKL. Polygon Ext. Sum Thm. 15 b° + 18 b° + 33 b° + 16 b° + 10 b° + 28 b° = 360° 120 b = 360 b=3 Holt Geometry Combine like terms. Divide both sides by 120.

6 -1 Properties and Attributes of Polygons Check It Out! Example 4 b Find the value of r in polygon JKLM. 4 r° + 7 r° + 5 r° + 8 r° = 360° Polygon Ext. Sum Thm. 24 r = 360 r = 15 Holt Geometry Combine like terms. Divide both sides by 24.