6 1 CHAPTER 6 Risk and Return The

























- Slides: 42

6 -1 CHAPTER 6 Risk and Return: The Basics n Basic return concepts n Basic risk concepts n Stand-alone risk n Portfolio (market) risk n Risk and return: CAPM/SML Copyright © 2005 by Harcourt, Inc All rights reserved.

6 -2 What are investment returns? n Investment returns measure the financial results of an investment. n Returns may be historical or prospective (anticipated). n Returns can be expressed in: l. Dollar terms. l. Percentage terms. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 -3 What is the return on an investment that costs $1, 000 and is sold after 1 year for $1, 100? n Dollar return: $ Received - $ Invested $1, 100 $1, 000 = $100. n Percentage return: $ Return/$ Invested $100/$1, 000 = 0. 10 = 10%. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 -4 What is investment risk? n Typically, investment returns are not known with certainty. n Investment risk pertains to the probability of earning a return less than that expected. n The greater the chance of a return far below the expected return, the greater the risk. Copyright © 2005 by Harcourt, Inc All rights reserved.

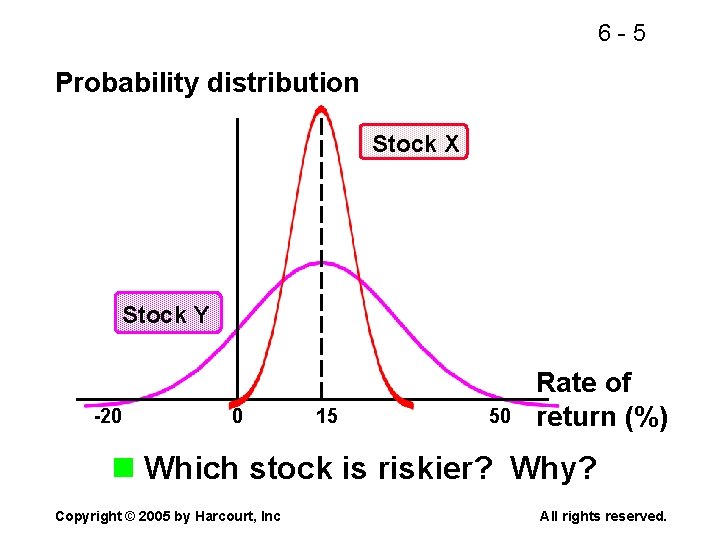
6 -5 Probability distribution Stock X Stock Y -20 0 15 50 Rate of return (%) n Which stock is riskier? Why? Copyright © 2005 by Harcourt, Inc All rights reserved.

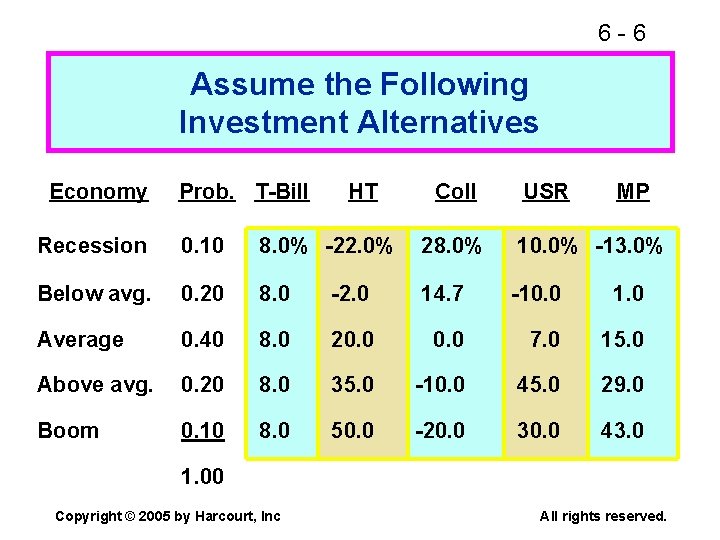
6 -6 Assume the Following Investment Alternatives Economy Prob. T-Bill HT Coll USR MP Recession 0. 10 8. 0% -22. 0% 28. 0% 10. 0% -13. 0% Below avg. 0. 20 8. 0 -2. 0 14. 7 -10. 0 1. 0 Average 0. 40 8. 0 20. 0 7. 0 15. 0 Above avg. 0. 20 8. 0 35. 0 -10. 0 45. 0 29. 0 Boom 0. 10 8. 0 50. 0 -20. 0 30. 0 43. 0 1. 00 Copyright © 2005 by Harcourt, Inc All rights reserved.

6 -7 What is unique about the T-bill return? n The T-bill will return 8% regardless of the state of the economy. n Is the T-bill riskless? Explain. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 -8 Do the returns of HT and Collections move with or counter to the economy? n HT moves with the economy, so it is positively correlated with the economy. This is the typical situation. n Collections moves counter to the economy. Such negative correlation is unusual. Copyright © 2005 by Harcourt, Inc All rights reserved.

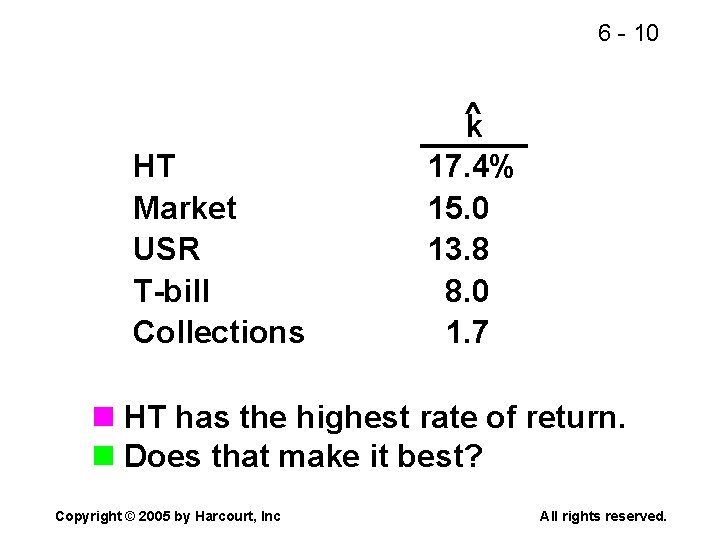
6 -9 Calculate the expected rate of return on each alternative. ^ k = expected rate of return. ^ k. HT = 0. 10(-22%) + 0. 20(-2%) + 0. 40(20%) + 0. 20(35%) + 0. 10(50%) = 17. 4%. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 10 HT Market USR T-bill Collections ^ k 17. 4% 15. 0 13. 8 8. 0 1. 7 n HT has the highest rate of return. n Does that make it best? Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 11 What is the standard deviation of returns for each alternative? Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 12 HT: = ((-22 - 17. 4)20. 10 + (-2 - 17. 4)20. 20 + (20 - 17. 4)20. 40 + (35 - 17. 4)20. 20 + (50 - 17. 4)20. 10)1/2 = 20. 0%. T-bills = 0. 0%. HT = 20. 0%. Copyright © 2005 by Harcourt, Inc Coll = 13. 4%. USR = 18. 8%. M = 15. 3%. All rights reserved.

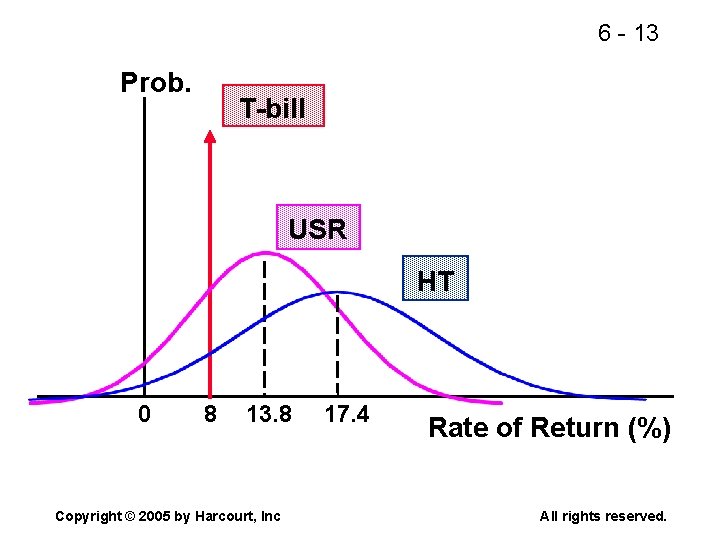
6 - 13 Prob. T-bill USR HT 0 8 13. 8 Copyright © 2005 by Harcourt, Inc 17. 4 Rate of Return (%) All rights reserved.

6 - 14 n Standard deviation measures the stand-alone risk of an investment. n The larger the standard deviation, the higher the probability that returns will be far below the expected return. n Coefficient of variation is an alternative measure of stand-alone risk. Copyright © 2005 by Harcourt, Inc All rights reserved.

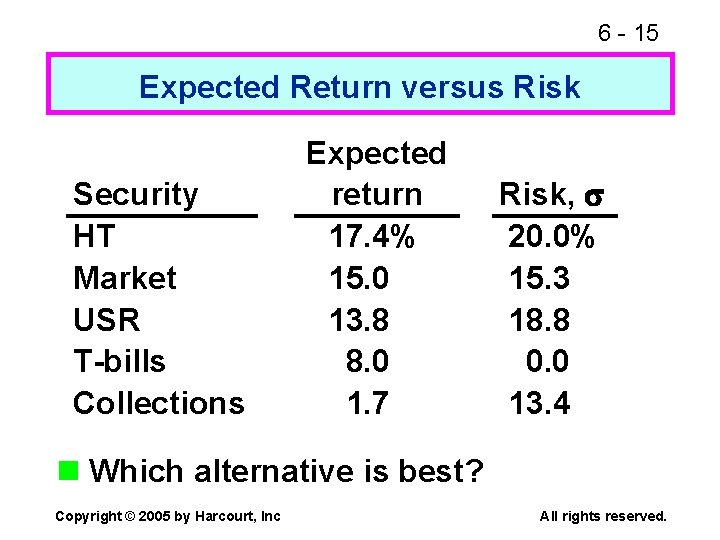
6 - 15 Expected Return versus Risk Security HT Market USR T-bills Collections Expected return 17. 4% 15. 0 13. 8 8. 0 1. 7 Risk, 20. 0% 15. 3 18. 8 0. 0 13. 4 n Which alternative is best? Copyright © 2005 by Harcourt, Inc All rights reserved.

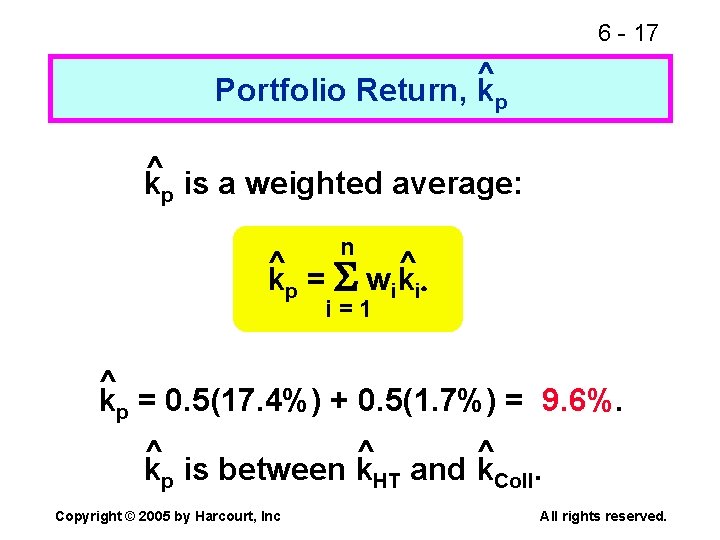
6 - 16 Portfolio Risk and Return Assume a two-stock portfolio with $50, 000 in HT and $50, 000 in Collections. ^ Calculate kp and p. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 17 ^ Portfolio Return, kp ^ kp is a weighted average: n ^ ^ kp = wiki i=1 ^ kp = 0. 5(17. 4%) + 0. 5(1. 7%) = 9. 6%. ^ ^ ^ kp is between k. HT and k. Coll. Copyright © 2005 by Harcourt, Inc All rights reserved.

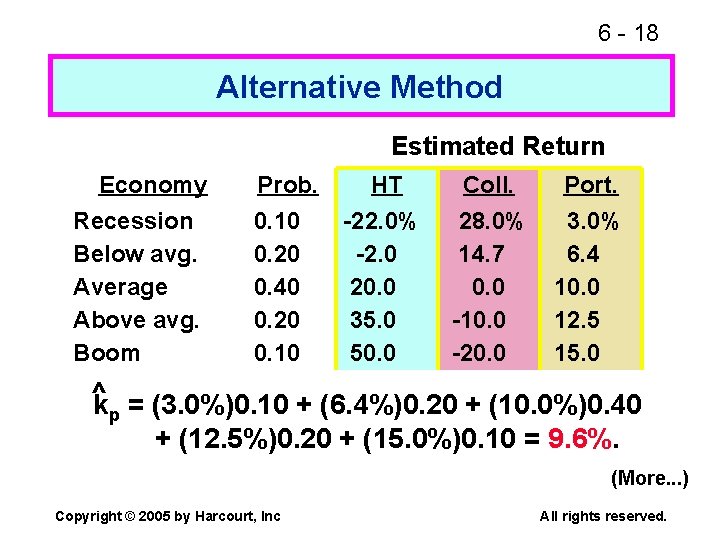
6 - 18 Alternative Method Estimated Return Economy Recession Below avg. Average Above avg. Boom Prob. 0. 10 0. 20 0. 40 0. 20 0. 10 HT -22. 0% -2. 0 20. 0 35. 0 50. 0 Coll. 28. 0% 14. 7 0. 0 -10. 0 -20. 0 Port. 3. 0% 6. 4 10. 0 12. 5 15. 0 ^ kp = (3. 0%)0. 10 + (6. 4%)0. 20 + (10. 0%)0. 40 + (12. 5%)0. 20 + (15. 0%)0. 10 = 9. 6%. (More. . . ) Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 19 n p = ((3. 0 - 9. 6)20. 10 + (6. 4 - 9. 6)20. 20 + (10. 0 - 9. 6)20. 40 + (12. 5 - 9. 6)20. 20 + (15. 0 - 9. 6)20. 10)1/2 = 3. 3%. n p is much lower than: leither stock (20% and 13. 4%). laverage of HT and Coll (16. 7%). n The portfolio provides average return but much lower risk. The key here is negative correlation. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 20 Two-Stock Portfolios n Two stocks can be combined to form a riskless portfolio if r = -1. 0. n Risk is not reduced at all if the two stocks have r = +1. 0. n In general, stocks have r 0. 65, so risk is lowered but not eliminated. n Investors typically hold many stocks. n What happens when r = 0? Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 21 What would happen to the risk of an average 1 -stock portfolio as more randomly selected stocks were added? n p would decrease because the added stocks would not be perfectly correlated, but ^ kp would remain relatively constant. Copyright © 2005 by Harcourt, Inc All rights reserved.

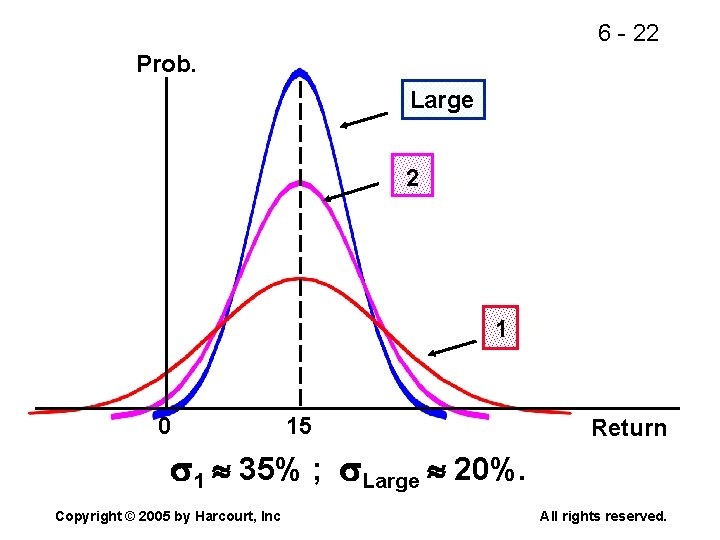
6 - 22 Prob. Large 2 1 0 15 Return 1 35% ; Large 20%. Copyright © 2005 by Harcourt, Inc All rights reserved.

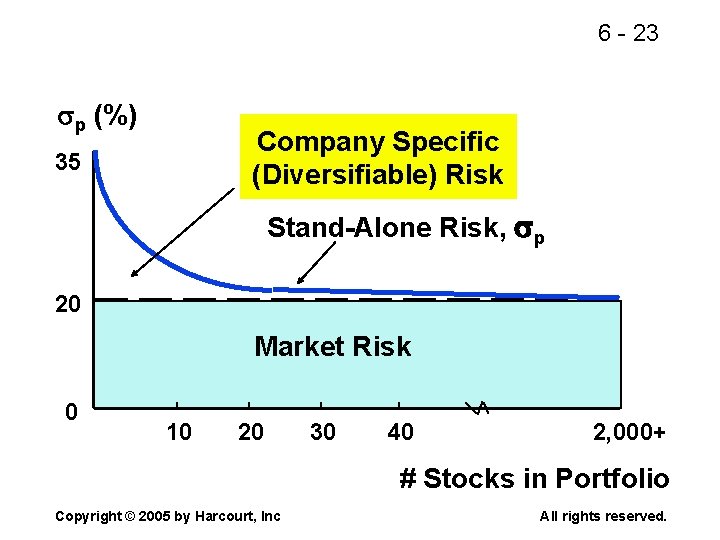
6 - 23 p (%) Company Specific (Diversifiable) Risk 35 Stand-Alone Risk, p 20 Market Risk 0 10 20 30 40 2, 000+ # Stocks in Portfolio Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 24 Stand-alone Market Diversifiable = risk +. risk Market risk is that part of a security’s stand-alone risk that cannot be eliminated by diversification. Firm-specific, or diversifiable, risk is that part of a security’s stand-alone risk that can be eliminated by diversification. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 25 Conclusions n As more stocks are added, each new stock has a smaller risk-reducing impact on the portfolio. n p falls very slowly after about 40 stocks are included. The lower limit for p is about 20% = M. n By forming well-diversified portfolios, investors can eliminate about half the riskiness of owning a single stock. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 26 Can an investor holding one stock earn a return commensurate with its risk? n No. Rational investors will minimize risk by holding portfolios. n They bear only market risk, so prices and returns reflect this lower risk. n The one-stock investor bears higher (stand-alone) risk, so the return is less than that required by the risk. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 27 How is market risk measured for individual securities? n Market risk, which is relevant for stocks held in well-diversified portfolios, is defined as the contribution of a security to the overall riskiness of the portfolio. n It is measured by a stock’s beta coefficient, which measures the stock’s volatility relative to the market. n What is the relevant risk for a stock held in isolation? Copyright © 2005 by Harcourt, Inc All rights reserved.

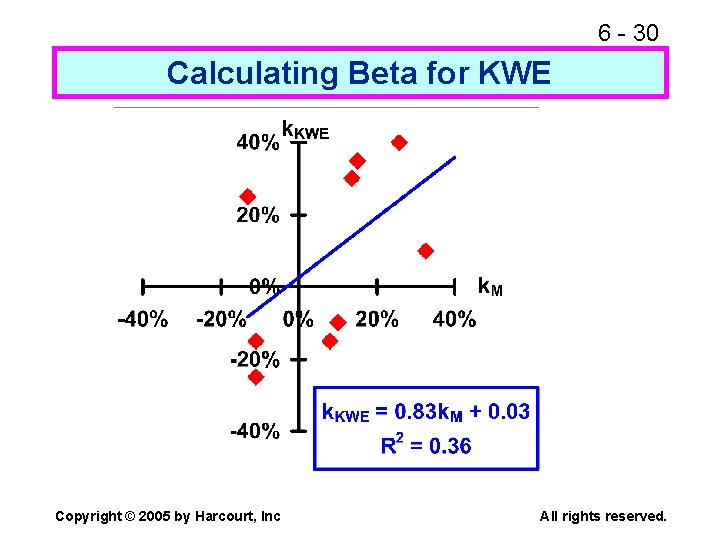
6 - 28 How are betas calculated? n Run a regression with returns on the stock in question plotted on the Y axis and returns on the market portfolio plotted on the X axis. n The slope of the regression line, which measures relative volatility, is defined as the stock’s beta coefficient, or b. Copyright © 2005 by Harcourt, Inc All rights reserved.

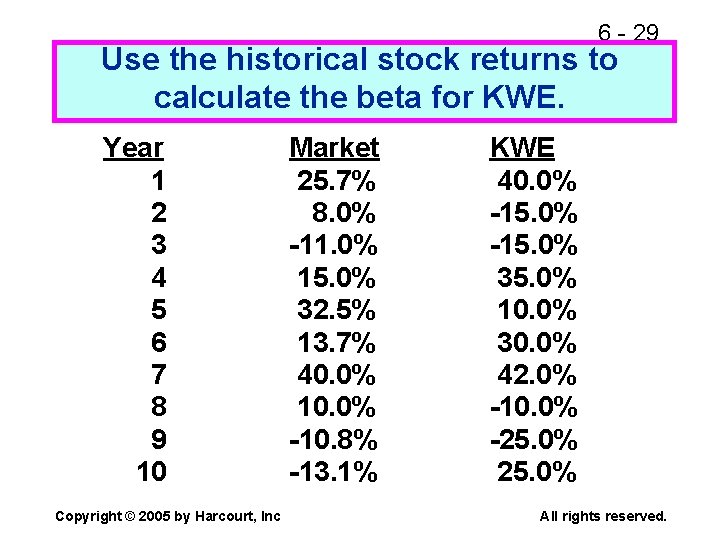
6 - 29 Use the historical stock returns to calculate the beta for KWE. Year 1 2 3 4 5 6 7 8 9 10 Copyright © 2005 by Harcourt, Inc Market 25. 7% 8. 0% -11. 0% 15. 0% 32. 5% 13. 7% 40. 0% 10. 0% -10. 8% -13. 1% KWE 40. 0% -15. 0% 35. 0% 10. 0% 30. 0% 42. 0% -10. 0% -25. 0% All rights reserved.

6 - 30 Calculating Beta for KWE Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 31 How is beta calculated? n The regression line, and hence beta, can be found using a calculator with a regression function or a spreadsheet program. In this example, b = 0. 83. n Analysts typically use four or five years’ of monthly returns to establish the regression line. Some use 52 weeks of weekly returns. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 32 How is beta interpreted? n If b = 1. 0, stock has average risk. n If b > 1. 0, stock is riskier than average. n If b < 1. 0, stock is less risky than average. n Most stocks have betas in the range of 0. 5 to 1. 5. n Can a stock have a negative beta? Copyright © 2005 by Harcourt, Inc All rights reserved.

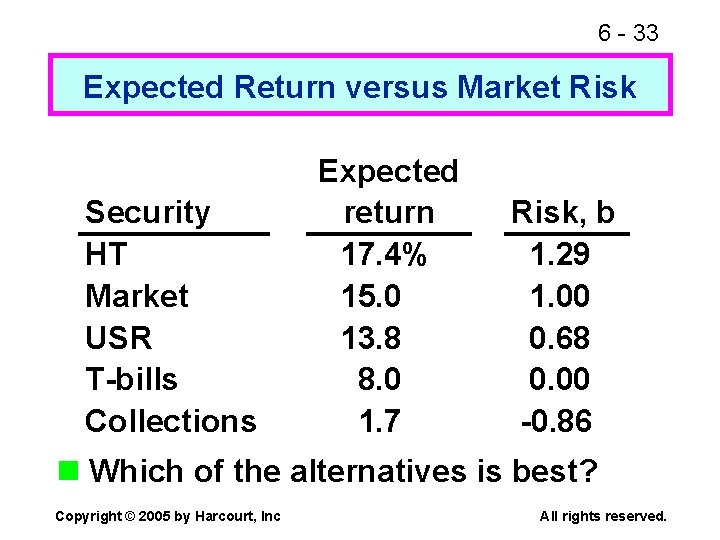
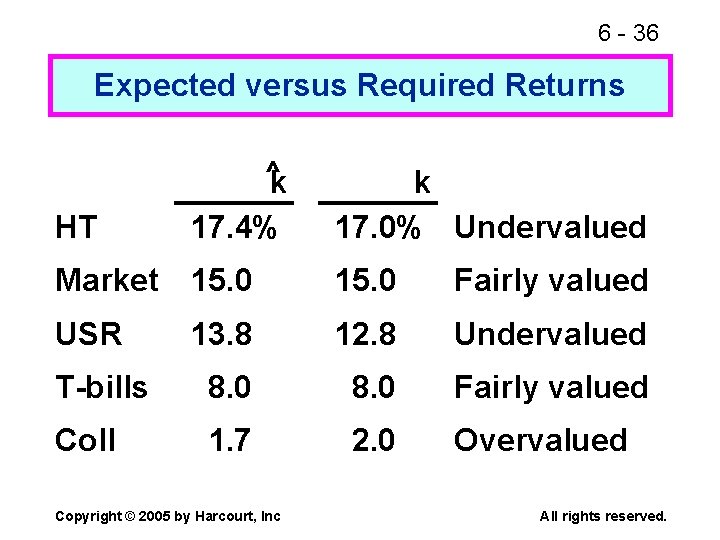
6 - 33 Expected Return versus Market Risk Security HT Market USR T-bills Collections Expected return 17. 4% 15. 0 13. 8 8. 0 1. 7 Risk, b 1. 29 1. 00 0. 68 0. 00 -0. 86 n Which of the alternatives is best? Copyright © 2005 by Harcourt, Inc All rights reserved.

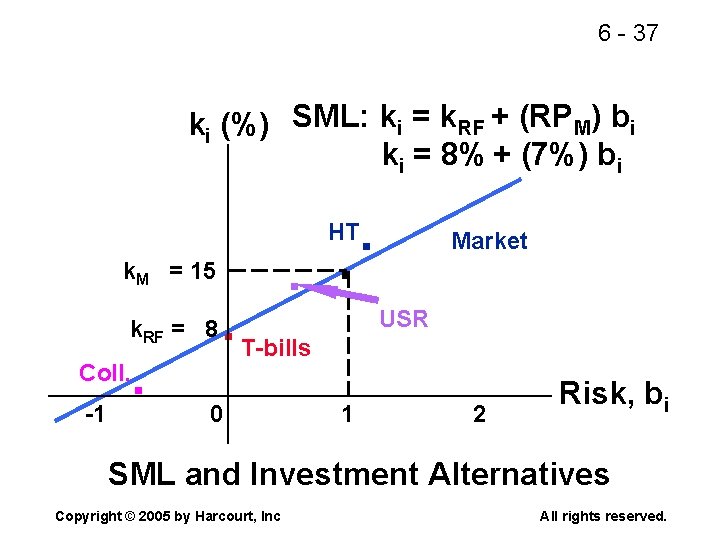
6 - 34 Use the SML to calculate each alternative’s required return. n The Security Market Line (SML) is part of the Capital Asset Pricing Model (CAPM). n SML: ki = k. RF + (RPM)bi. n Assume k. RF = 8%; ^k. M = 15%. n RPM = (k. M - k. RF) = 15% - 8% = 7%. Copyright © 2005 by Harcourt, Inc All rights reserved.

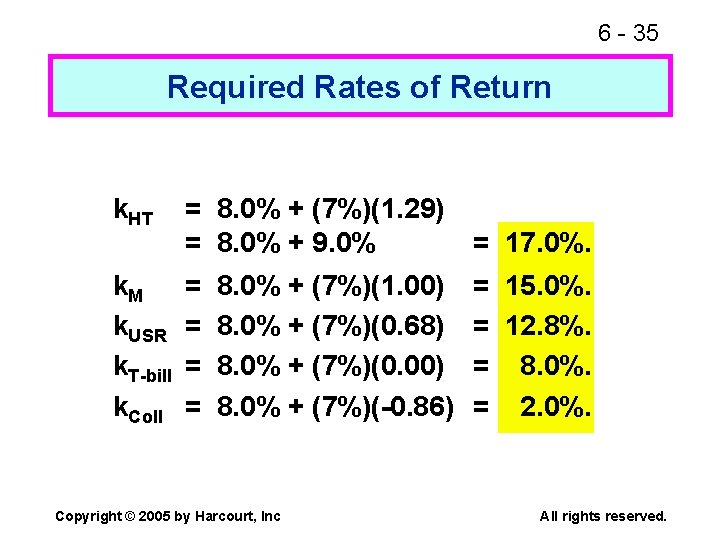
6 - 35 Required Rates of Return k. HT = 8. 0% + (7%)(1. 29) = 8. 0% + 9. 0% = 17. 0%. k. M k. USR k. T-bill k. Coll = = = 15. 0%. = 12. 8%. = 8. 0%. = 2. 0%. 8. 0% + (7%)(1. 00) 8. 0% + (7%)(0. 68) 8. 0% + (7%)(0. 00) 8. 0% + (7%)(-0. 86) Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 36 Expected versus Required Returns ^k HT 17. 4% k 17. 0% Undervalued Market 15. 0 Fairly valued USR 13. 8 12. 8 Undervalued T-bills 8. 0 Fairly valued Coll 1. 7 2. 0 Overvalued Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 37 ki (%) SML: ki = k. RF + (RPM) bi ki = 8% + (7%) bi . HT k. M = 15 k. RF = 8 . Coll. -1 . . . T-bills 0 Market USR 1 2 Risk, bi SML and Investment Alternatives Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 38 Calculate beta for a portfolio with 50% HT and 50% Collections bp = Weighted average = 0. 5(b. HT) + 0. 5(b. Coll) = 0. 5(1. 29) + 0. 5(-0. 86) = 0. 22. Copyright © 2005 by Harcourt, Inc All rights reserved.

6 - 39 What is the required rate of return on the HT/Collections portfolio? kp = Weighted average k = 0. 5(17%) + 0. 5(2%) = 9. 5%. Or use SML: kp = k. RF + (RPM) bp = 8. 0% + 7%(0. 22) = 9. 5%. Copyright © 2005 by Harcourt, Inc All rights reserved.

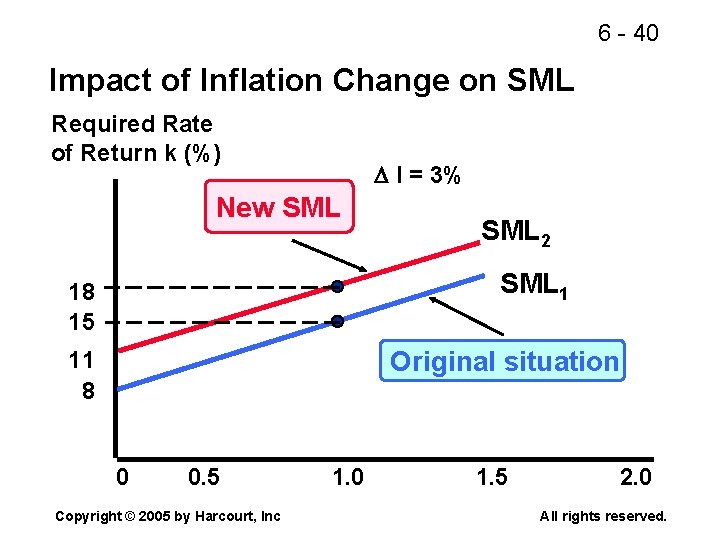
6 - 40 Impact of Inflation Change on SML Required Rate of Return k (%) I = 3% New SML 2 SML 1 18 15 Original situation 11 8 0 0. 5 Copyright © 2005 by Harcourt, Inc 1. 0 1. 5 2. 0 All rights reserved.

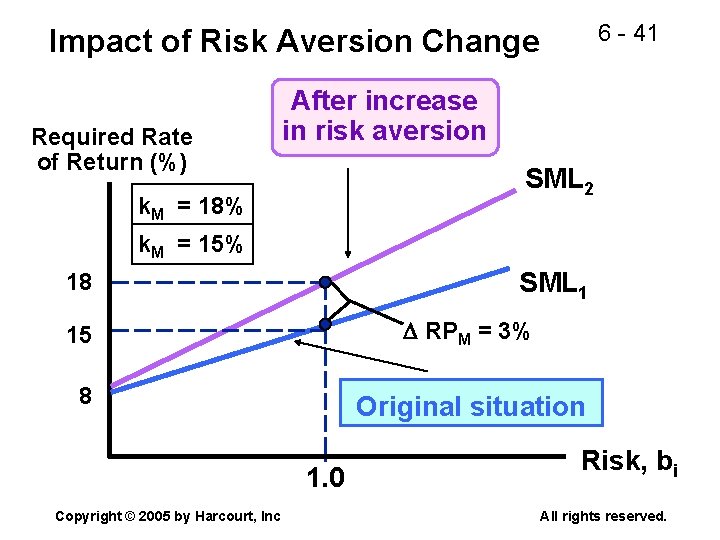
6 - 41 Impact of Risk Aversion Change Required Rate of Return (%) After increase in risk aversion SML 2 k. M = 18% k. M = 15% SML 1 18 15 RPM = 3% 8 Original situation 1. 0 Copyright © 2005 by Harcourt, Inc Risk, bi All rights reserved.

6 - 42 Has the CAPM been verified through empirical tests? n No. The statistical tests have problems that make empirical verification virtually impossible. n Investors may be concerned about both stand-alone risk and market risk. n Furthermore, investors’ required returns are based on future risk, but betas are based on historical data. Copyright © 2005 by Harcourt, Inc All rights reserved.