5 You can do it Chapter 1 Matter

5

You can do it.

Chapter 1 Matter and Measurement

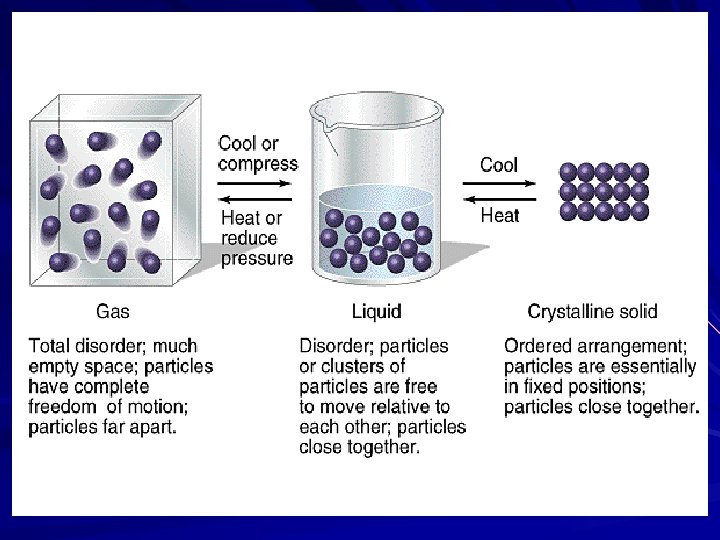
States of Matter

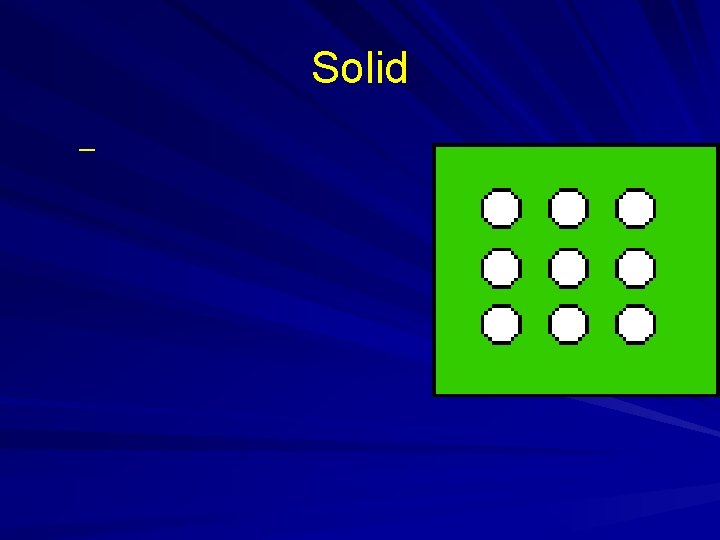
Solid –

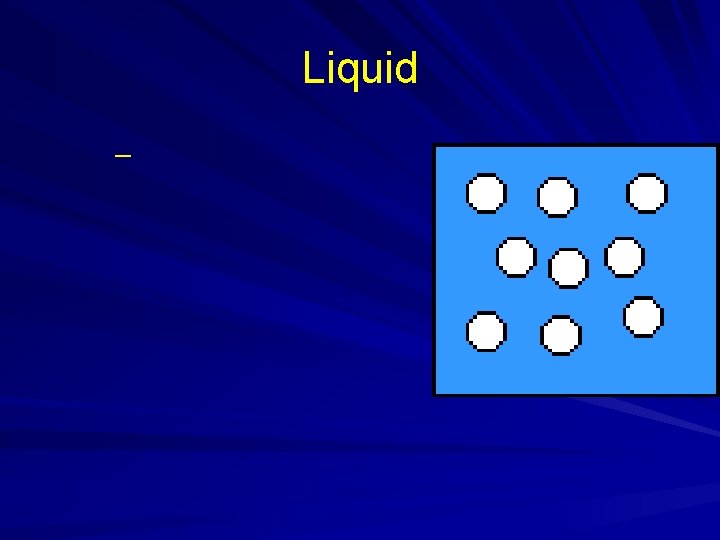
Liquid –

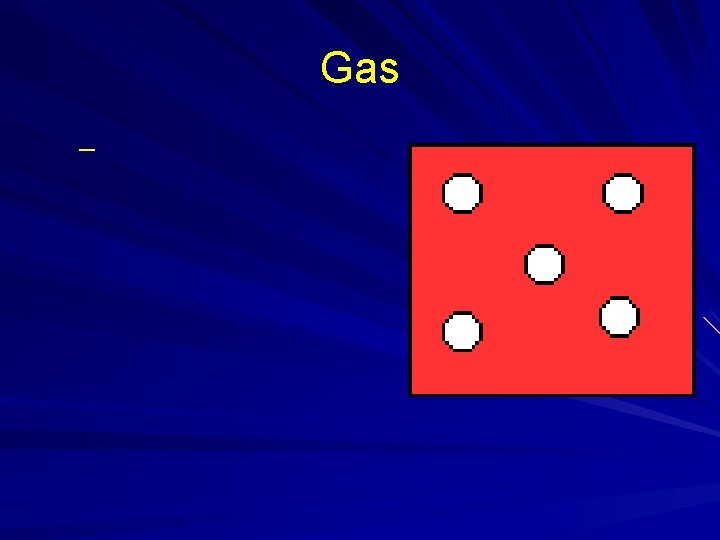
Gas –

Plasma

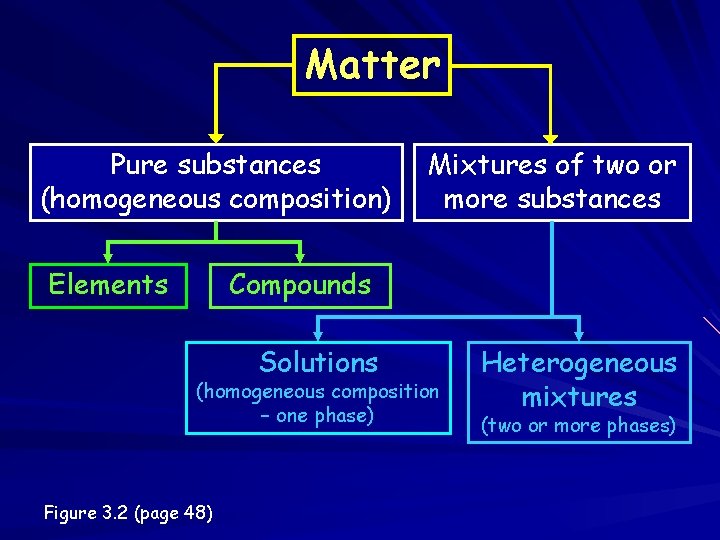
Matter Pure substances (homogeneous composition) Elements Mixtures of two or more substances Compounds Solutions (homogeneous composition – one phase) Figure 3. 2 (page 48) Heterogeneous mixtures (two or more phases)

Classifying Substances

Mixtures Homogeneous – – – Heterogeneous – – –

Pure substance A particular kind of matter with a definite, fixed composition – Elements – Compounds

Compounds Two or more elements New Definite Can be

How would you classify? Gatorade Caesar salad Water Coffee An iron nail Air Milk

Methods of Separation Do not cause chemical changes

Filtration Used for Gravity Vacuum

Sublimation

Evaporation Solutions…

Distillation Relies on

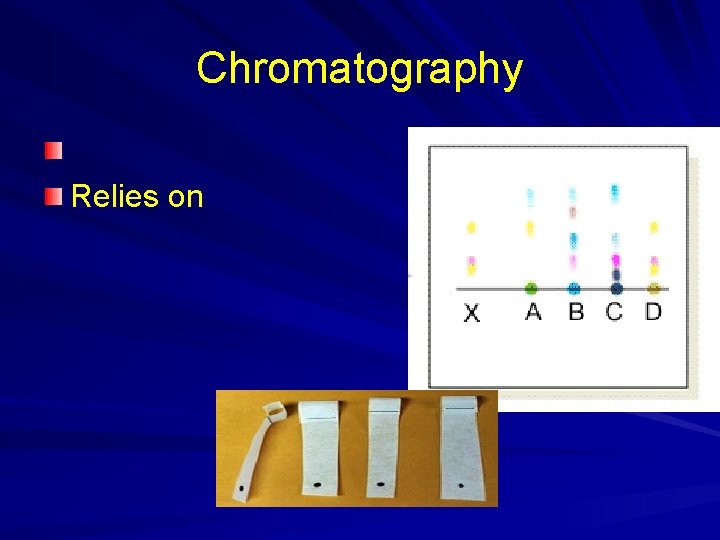
Chromatography Relies on

Decantation

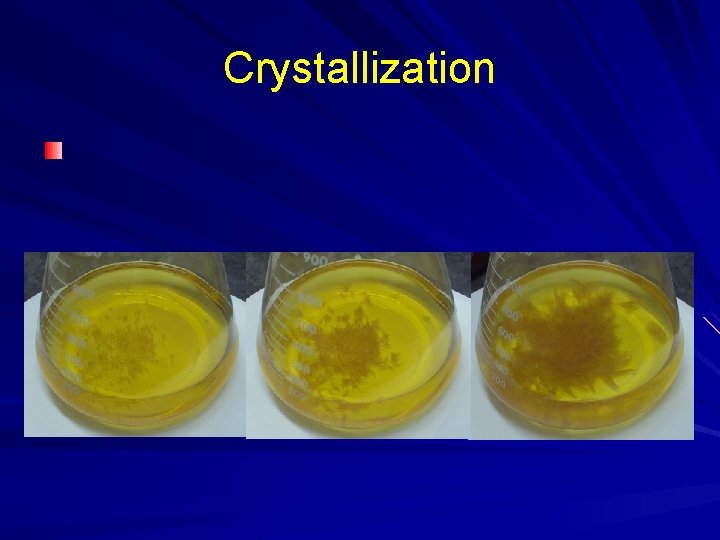
Crystallization

5

The Metric System The International System of Units Standards of measurement Base units (7) – see Table 1. 4 pg 14 1. 2. 3. 4. 5. 6. 7. MASS: LENGTH: TIME: COUNT, QUANTITY: TEMPERATURE: ELECTRIC CURRENT: LUMINOUS INSTENSITY:

The Metric System Derived Units: § AREA: § VOLUME: § ENERGY: § FORCE: § PRESSURE: § POWER: § VOLTAGE: § FREQUENCY: § ELECTRIC CHARGE:

Density Common ratio used in chemistry Physical property of a substance Solid – g/cm 3 Liquid – g/m. L Gas D= SI units: kg/m 3 – g/L Can change due to temperature and/or pressure changes

Density 1. Find the density of a piece of metal with a volume of 2. 7 cm 3 and a mass of 10. 8 g. 2. Determine the mass of an object with a density of 0. 24 g/cm 3 and a volume of 2 cm 3.

The Metric System Metric Prefixes – make base unit larger or smaller Table 1. 5 – pg 14 Based on 10 Math method vs. “Stairs”

Conversion Practice Convert a volume of 12 microliters into centiliters Express a distance of 15 meters in kilometers Convert 83 cm into meters Which is the longer amount of time, 1351 ps or 1. 2 ns? Convert 16 d. L into L

Uncertainty in Measurement Why are digits in measurements uncertain? 1. Instruments never completely free of flaws 2. Always involves estimation v Choose the right instrument for the job v May be estimated for you (electronic scales) v Scale is marked but you estimate the inbetween

Uncertainty in Measurement Precision: getting the same result again and again under same conditions Accuracy: close to accepted value

Significant Digits All digits known with certainty plus one final digit which is uncertain (or estimated) All non-zeros A zero is significant when : – It is A zero is not significant when: – It is

Significant Digits - PRACTICE How many significant digits? 1. 54. 23 2. 23. 00005 3. 0. 0004 4. 35000 5. 0. 000504 6. 45. 623200 7. 5, 000 8. 4, 000. 1

Significant Digits - Calculations Addition and Subtraction – Round answer to have final digit in the SAME PLACE as the last digit in the LEAST ACCURATE MEASUREMENT 1. 21 + 5. 002 + 10. = 34. 5 + 12. 45 + 23. 0505 = 186. 31 + 11. 1 = 12. 0231 + 3. 86 = 0. 100012 + 120. = 1200 + 12 + 15 + 0. 5 =

Significant Digits - Calculations Multiplication and Division – The answer has as many sig figs as the number with the fewest sig figs 14. 8 x 3. 1 = 18. 2 x 3. 0 = 52/1. 5 = 321. 868783 x 1 = 2400 x 2. 123 = 15000/12. 354 =

Scientific Notation Convenient way of writing very large or very small numbers and showing only significant figures Number between 1 & 10 with a power of ten 5120 becomes 5. 12 x 103 Move decimal point in original number to make number 1 -10 Move left = +; move right = -

Scientific Notation Practice 123, 000 = 0. 000045 = 23. 45 = 0. 000003 = 1, 000 =

Scientific Notation Math with: – Use the EE or EXP button on your calculator. – For example: (1. 25 x 105) (5. 25 x 102) Keystrokes are: Or:

Types of Measurements Mass – – Expressed in – Does Weight – – Expressed in same units –

Types of Measurements Volume – – Cubic – Many instruments to measure Temperature – – Kelvin – Degrees Celsius – Degress Farenheit

Conversion Factors Enable movement between metric system and “English” system See back cover of book and Appendix III Common conversions you should memorize – – – 1 inch = 2. 54 cm 1 mile = 1. 609 km 1 kg = 2. 20 pounds 1 m. L = 1 cm 3 0 K = -273. 15 0 C 0 F = 1. 8(0 C) + 32

5

Dimensional Analysis (Problem Solving) Remember: ALWAYS use UNITS OF MEASUREMENT in your work!!! A technique of converting between units – Same system (metrics) – Different systems (inches to meters) – Chemical equations…. later chapters…

Dimensional Analysis (Problem Solving) Conversion Factors: ratio derived from the equality between 2 different units 3 feet = 1 1 yard 1 dollar = 1 4 quarters CF can be written either way 1 minute = 1 60 seconds = 1 1 minute

Dimensional Analysis (Problem Solving) The “t” method unit given unit wanted = unit wanted unit given Conversion Factor Example: How many liters are in 125. 6 gallons?

Dimensional Analysis (Problem Solving) How many seconds are in 4. 15 hours? If a student needs 1. 5 m. L of water, how many cups does he need?