5 Trees ISC 241 Data Structures Dr Jehad

(5) Trees ISC 241 Data Structures Dr. Jehad Al Dallal Spring 2017/2018 © 2009 Jehad Al Dallal Trees 1

Outlines n Tree n n Binary tree n n n What is a tree? Tree traversal Linked list representation Applications Properties Representation and implementation Traversal Arithmetic Expression tree Binary Search tree © 2009 Jehad Al Dallal Trees 2

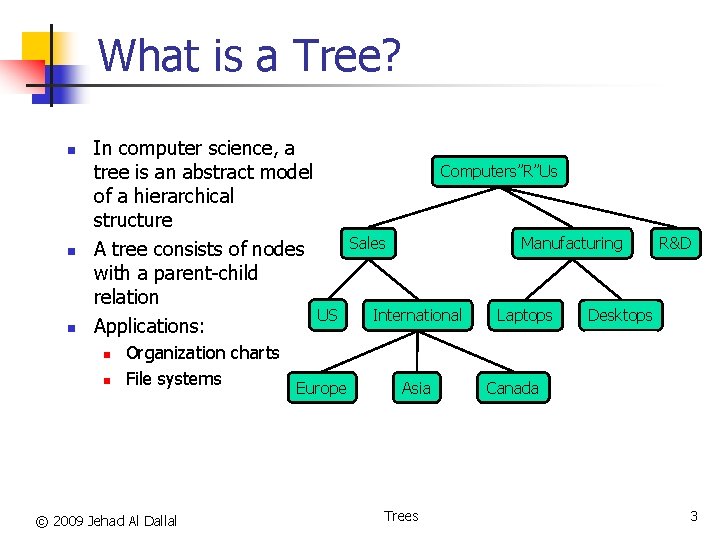
What is a Tree? n n n In computer science, a tree is an abstract model of a hierarchical structure A tree consists of nodes with a parent-child relation US Applications: n n Organization charts File systems Europe © 2009 Jehad Al Dallal Computers”R”Us Sales Manufacturing International Asia Trees Laptops R&D Desktops Canada 3

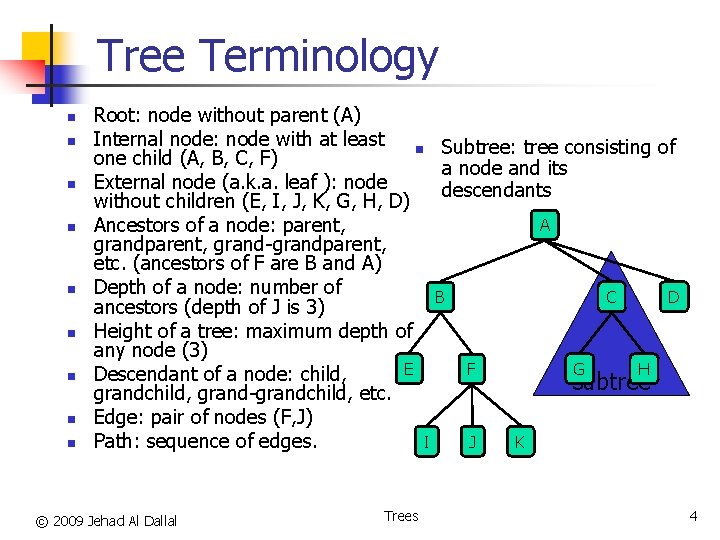
Tree Terminology n n n n n Root: node without parent (A) Internal node: node with at least n Subtree: tree consisting of one child (A, B, C, F) a node and its External node (a. k. a. leaf ): node descendants without children (E, I, J, K, G, H, D) A Ancestors of a node: parent, grand-grandparent, etc. (ancestors of F are B and A) Depth of a node: number of B C D ancestors (depth of J is 3) Height of a tree: maximum depth of any node (3) E F G H Descendant of a node: child, subtree grandchild, grand-grandchild, etc. Edge: pair of nodes (F, J) I J K Path: sequence of edges. © 2009 Jehad Al Dallal Trees 4

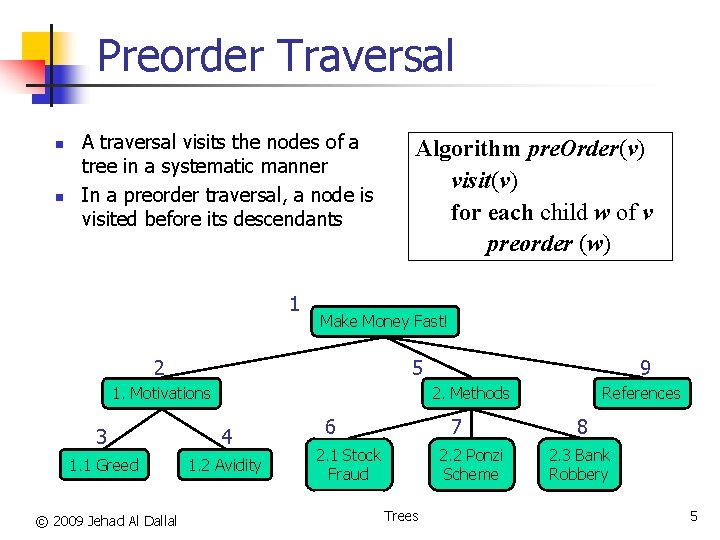
Preorder Traversal n n A traversal visits the nodes of a tree in a systematic manner In a preorder traversal, a node is visited before its descendants 1 Algorithm pre. Order(v) visit(v) for each child w of v preorder (w) Make Money Fast! 2 5 1. Motivations 2. Methods 3 4 1. 1 Greed 1. 2 Avidity © 2009 Jehad Al Dallal 9 6 7 2. 1 Stock Fraud 2. 2 Ponzi Scheme Trees References 8 2. 3 Bank Robbery 5

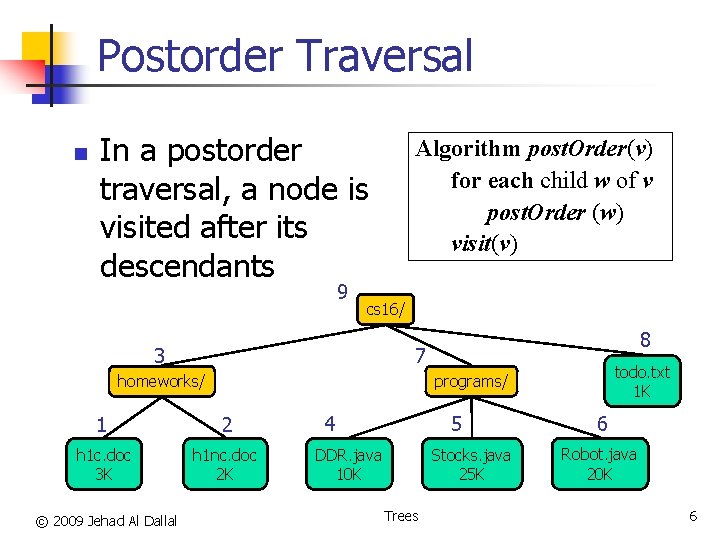
Postorder Traversal n In a postorder traversal, a node is visited after its descendants 9 Algorithm post. Order(v) for each child w of v post. Order (w) visit(v) cs 16/ 3 7 homeworks/ todo. txt 1 K programs/ 1 2 h 1 c. doc 3 K h 1 nc. doc 2 K © 2009 Jehad Al Dallal 8 4 5 DDR. java 10 K Stocks. java 25 K Trees 6 Robot. java 20 K 6

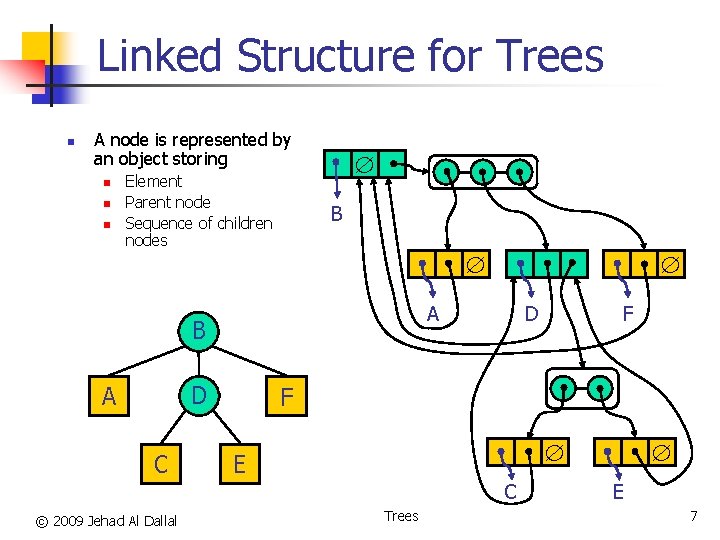
Linked Structure for Trees n A node is represented by an object storing n n n Element Parent node Sequence of children nodes B A B D A C D F E C © 2009 Jehad Al Dallal F Trees E 7

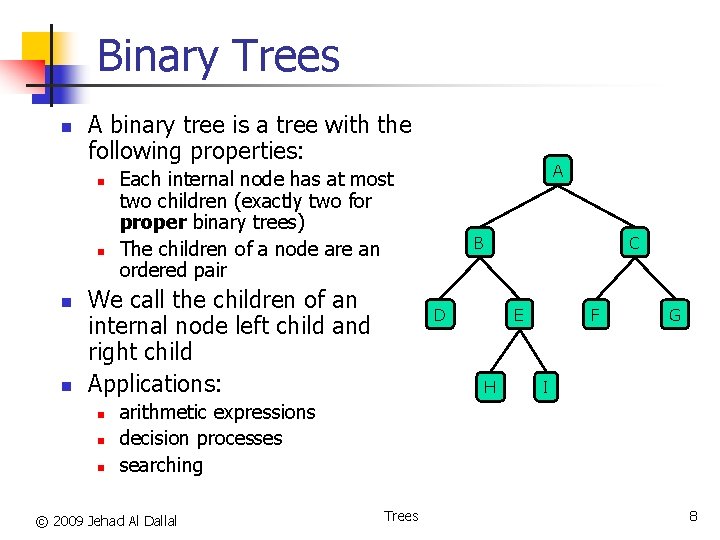
Binary Trees n A binary tree is a tree with the following properties: n n We call the children of an internal node left child and right child Applications: n n n A Each internal node has at most two children (exactly two for proper binary trees) The children of a node are an ordered pair C B D F E H G I arithmetic expressions decision processes searching © 2009 Jehad Al Dallal Trees 8

Arithmetic Expression Tree n Binary tree associated with an arithmetic expression n internal nodes: operators external nodes: operands Example: arithmetic expression tree for the expression (2 (a - 1) + (3 b)) + - 2 a © 2009 Jehad Al Dallal 3 b 1 Trees 9

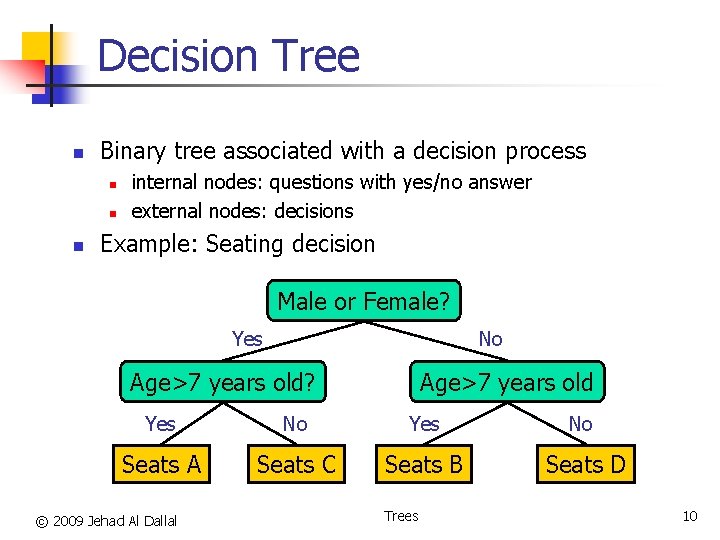
Decision Tree n Binary tree associated with a decision process n n n internal nodes: questions with yes/no answer external nodes: decisions Example: Seating decision Male or Female? No Yes Age>7 years old? Age>7 years old Yes No Seats A Seats C Seats B Seats D © 2009 Jehad Al Dallal Trees 10

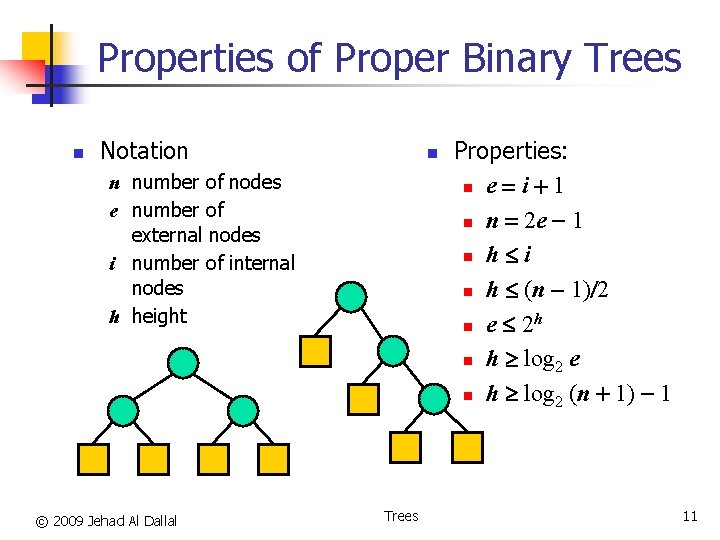
Properties of Proper Binary Trees n Notation n n number of nodes e number of external nodes i number of internal nodes h height © 2009 Jehad Al Dallal Trees Properties: n e = i + 1 n n = 2 e - 1 n h i n h (n - 1)/2 h n e 2 n h log 2 e n h log 2 (n + 1) - 1 11

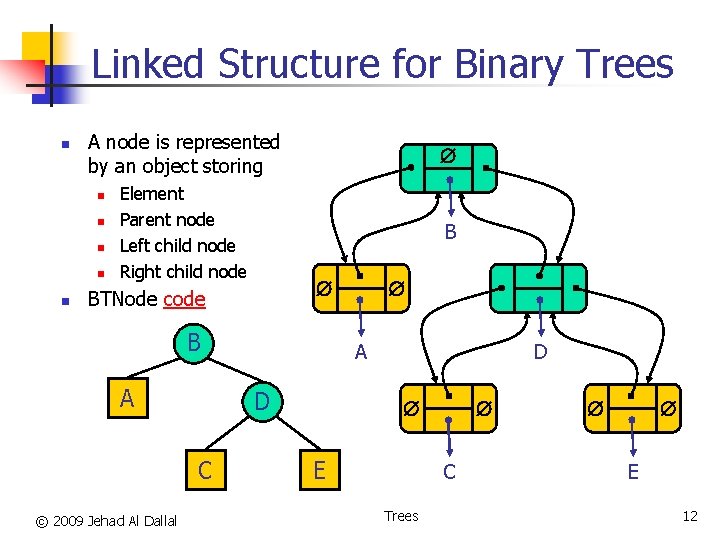
Linked Structure for Binary Trees n A node is represented by an object storing Element Parent node Left child node Right child node B n n n BTNode code B A © 2009 Jehad Al Dallal A D C D E C Trees E 12

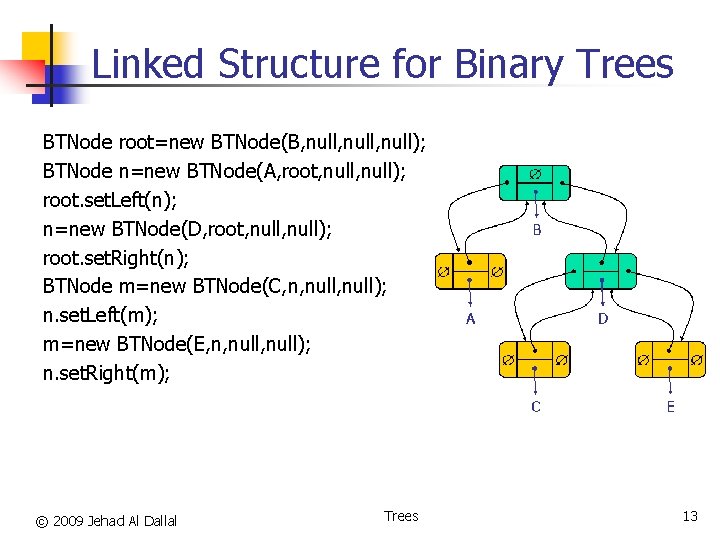
Linked Structure for Binary Trees BTNode root=new BTNode(B, null, null); BTNode n=new BTNode(A, root, null); root. set. Left(n); n=new BTNode(D, root, null); root. set. Right(n); BTNode m=new BTNode(C, n, null); n. set. Left(m); m=new BTNode(E, n, null); n. set. Right(m); © 2009 Jehad Al Dallal Trees 13

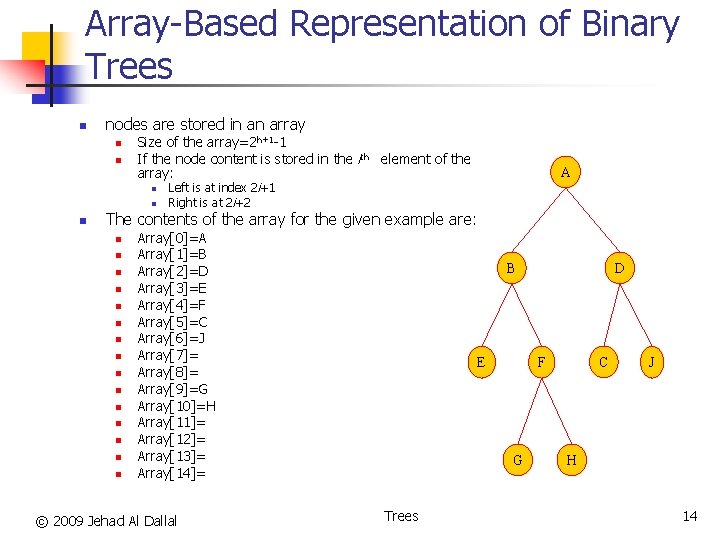
Array-Based Representation of Binary Trees n nodes are stored in an array n n Size of the array=2 h+1 -1 If the node content is stored in the ith element of the array: n n n A Left is at index 2 i+1 Right is at 2 i+2 The contents of the array for the given example are: n n n n Array[0]=A Array[1]=B Array[2]=D Array[3]=E Array[4]=F Array[5]=C Array[6]=J Array[7]= Array[8]= Array[9]=G Array[10]=H Array[11]= Array[12]= Array[13]= Array[14]= © 2009 Jehad Al Dallal B E C F G Trees D J H 14

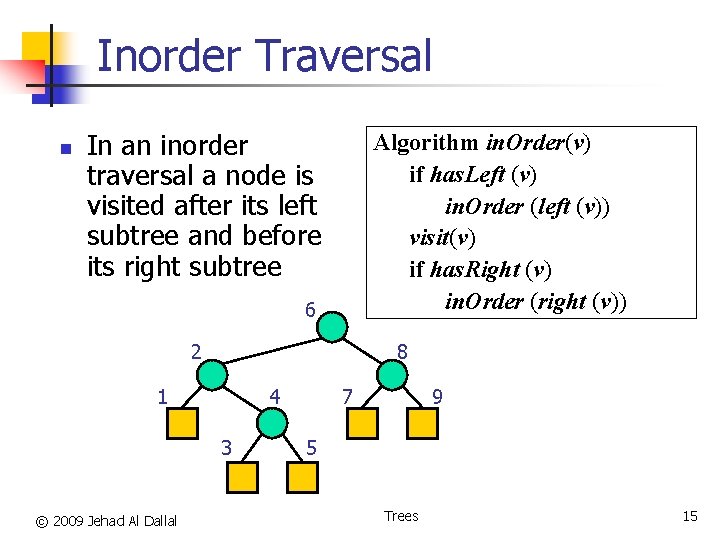
Inorder Traversal n In an inorder traversal a node is visited after its left subtree and before its right subtree Algorithm in. Order(v) if has. Left (v) in. Order (left (v)) visit(v) if has. Right (v) in. Order (right (v)) 6 2 8 1 4 3 © 2009 Jehad Al Dallal 7 9 5 Trees 15

Print Arithmetic Expressions n Specialization of an inorder traversal n n n print operand or operator when visiting node print “(“ before traversing left subtree print “)“ after traversing right subtree + - 2 a © 2009 Jehad Al Dallal 3 1 b Algorithm print. Expression(v) if has. Left (v) print(“(’’) in. Order (left(v)) print(v. element ()) if has. Right (v) in. Order (right(v)) print (“)’’) ((2 (a - 1)) + (3 b)) Trees 16

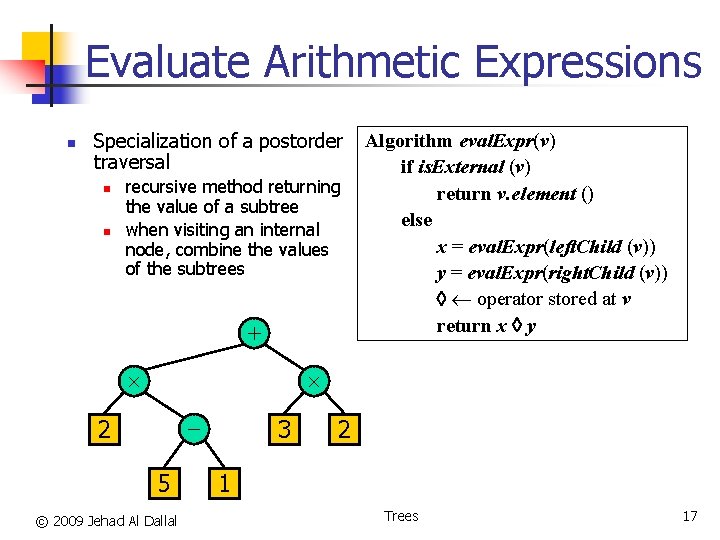
Evaluate Arithmetic Expressions n Specialization of a postorder traversal n n recursive method returning the value of a subtree when visiting an internal node, combine the values of the subtrees + Algorithm eval. Expr(v) if is. External (v) return v. element () else x = eval. Expr(left. Child (v)) y = eval. Expr(right. Child (v)) operator stored at v return x y - 2 5 © 2009 Jehad Al Dallal 3 2 1 Trees 17

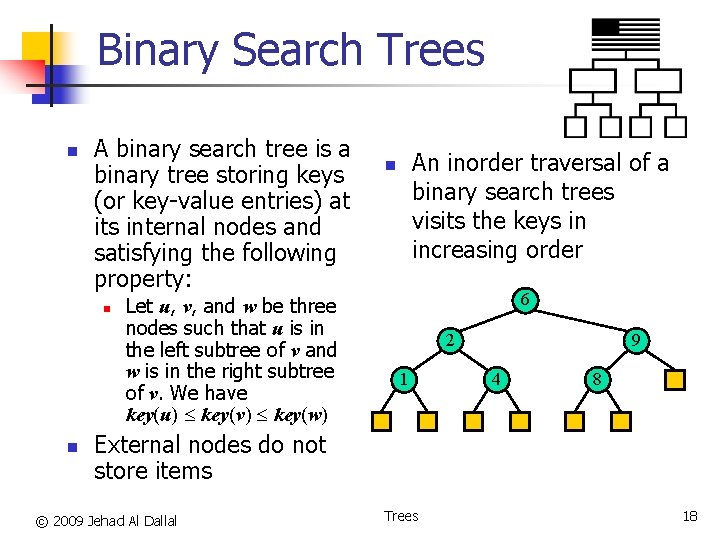
Binary Search Trees n A binary search tree is a binary tree storing keys (or key-value entries) at its internal nodes and satisfying the following property: n n Let u, v, and w be three nodes such that u is in the left subtree of v and w is in the right subtree of v. We have key(u) key(v) key(w) An inorder traversal of a binary search trees visits the keys in increasing order n 6 2 1 9 4 8 External nodes do not store items © 2009 Jehad Al Dallal Trees 18

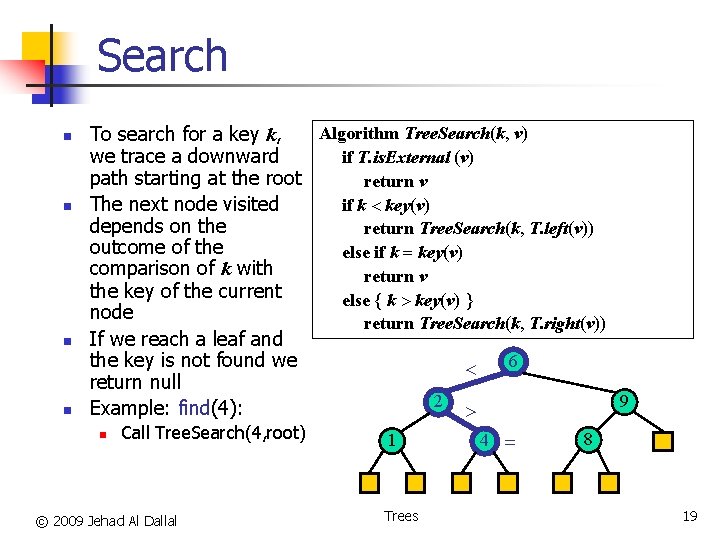
Search n n Algorithm Tree. Search(k, v) To search for a key k, if T. is. External (v) we trace a downward path starting at the root return v if k < key(v) The next node visited depends on the return Tree. Search(k, T. left(v)) outcome of the else if k = key(v) comparison of k with return v the key of the current else { k > key(v) } node return Tree. Search(k, T. right(v)) If we reach a leaf and 6 the key is not found we < return null 2 9 Example: find(4): > n Call Tree. Search(4, root) © 2009 Jehad Al Dallal 1 Trees 4 = 8 19

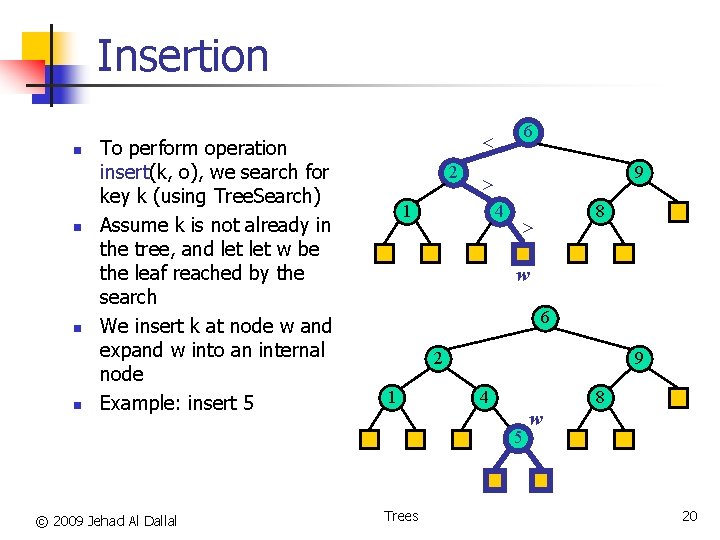
Insertion n n To perform operation insert(k, o), we search for key k (using Tree. Search) Assume k is not already in the tree, and let w be the leaf reached by the search We insert k at node w and expand w into an internal node Example: insert 5 6 < 2 9 > 1 4 > w 6 2 1 9 4 8 5 © 2009 Jehad Al Dallal 8 Trees w 20

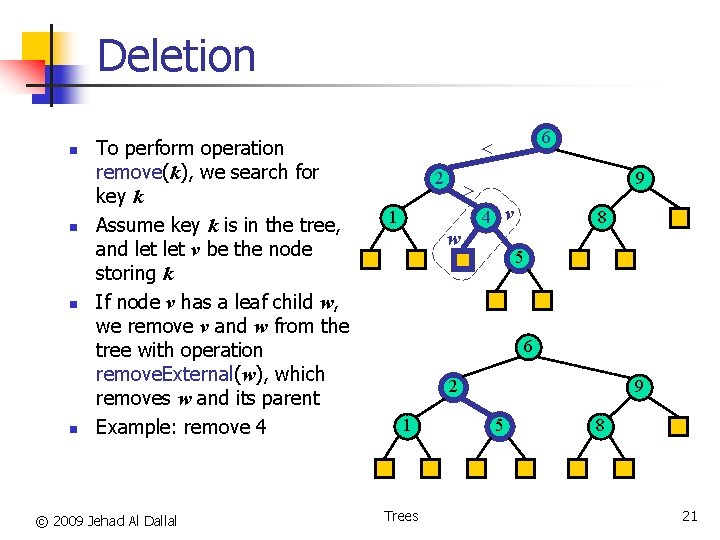
Deletion n n To perform operation remove(k), we search for key k Assume key k is in the tree, and let v be the node storing k If node v has a leaf child w, we remove v and w from the tree with operation remove. External(w), which removes w and its parent Example: remove 4 © 2009 Jehad Al Dallal 6 < 2 9 > 4 v 1 w 8 5 6 2 1 Trees 9 5 8 21

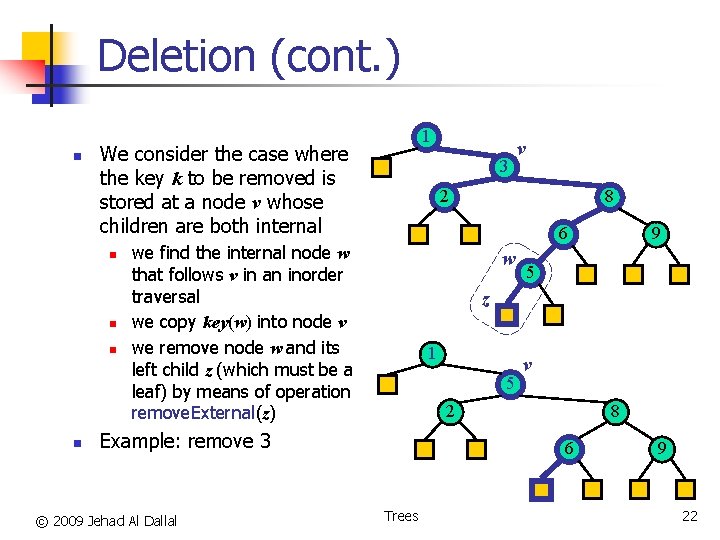
Deletion (cont. ) n We consider the case where the key k to be removed is stored at a node v whose children are both internal n n 1 3 2 8 6 we find the internal node w that follows v in an inorder traversal we copy key(w) into node v we remove node w and its left child z (which must be a leaf) by means of operation remove. External(z) w 9 5 z 1 5 v 2 Example: remove 3 © 2009 Jehad Al Dallal v 8 6 Trees 9 22

Reference n Data Structures and Algorithms in Java, Michael T. Goodrich and Roberto Tamassia, John Wiley & Sons, Inc, 6 th Edition, 2015 © 2009 Jehad Al Dallal Trees 23