5 Sensitivity change by examples Max f 3

5. Sensitivity – change by examples Max f = 3 x 1 + 2 x 2 6 x 1 + 4 x 2 ≤ 24 b 2 10 x 1 + 3 x 2 ≤ 30 x 1, x 2 0 Max Cj C 31 C 22 0 0 x 1 x 2 sl 1 sl 2 bi C 1 cc. B 1 B 1==0 2 2 x. B 1 =x 21 B 1=sl 6 41 1 ¼ 0 24 6 2 x. B 2=sl 2 10 30 0 -¾ 1 30 12 fj 03 C 2 C 0 22 ¼½ 0 C 2 0 Cj-fj 30 20 0 -½ 0 i c. B =00 cc. B 2= x. B Non-basic: C 1 – 3 ≤ 0 → C 1 ≤ 3 Basic: 3 – (3/2)C 2 ≤ 0 → C 2 2 and – ¼C 2 ≤ 0 → C 2 0 i ∑ic. Bibi= 12 x 2 sl 1 sl 2 4 0 1 0 3 1 0 1 x 2 sl 1 sl 2 1 0 1/4 0 ÷ 4 0 1 -3/4 1 ×(-3)+ Right-hand Side: B-1 NXN + XB = B-1[b] → XB = B-1[b] b 2 18 2021/10/18 1

5. Sensitivity – change by examples cont’ MAX 1. 417 A + 1. 43 B + 1. 85 C + 2. 138 D + 1. 7 E SUBJECT TO 2) 12 A + 7 B + 8 C + 10 D + 7 E <= 7680 3) 8 A + 9 B + 4 C + 11 E <= 7680 4) 5 A + 10 B + 7 C + 3 D + 2 E <= 7680 THE TABLEAU ROW (BASIS) A B C 1 ART 1. 417 1. 43 1. 85 2 (1. 85) C 1. 267. 233 1. 000 3 (1. 7) E. 267. 733. 000 4 (0) SLK 4 -4. 400 6. 900. 000 D E SLK 2 2. 138 1. 7 0 1. 833. 000. 183666 -. 667 1. 000 -. 067 -8. 500. 000 -1. 150 SLK 3 SLK 4 0 0 -. 117. 000. 133. 000. 550 1. 000 1817 512 3072 (1) Optimal Solution is to produce (A*, B*, C*, D*, E*) = (0, 0, 512) (2) Objective function value Z* = $ 1817 2021/10/18 2
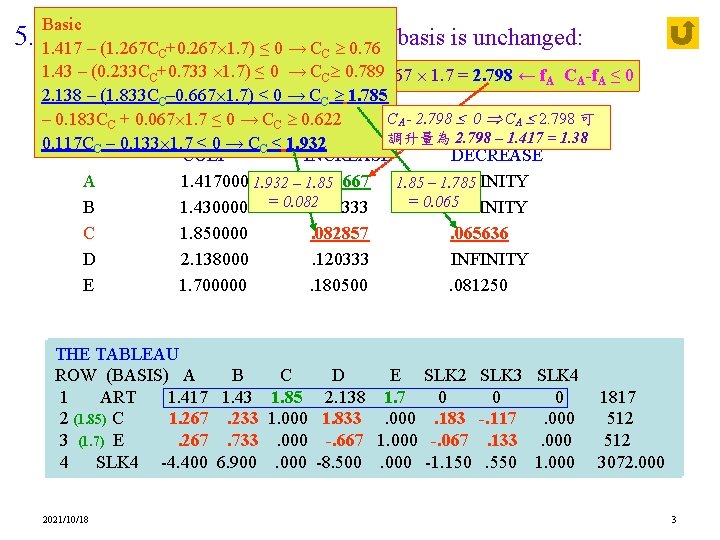
Basic 5. 11. 417 Sensitivity - Ranges≤ in the basis is unchanged: – (1. 267 CC+0. 267 1. 7) 0 →which CC 0. 76 1. 43 – (0. 233 CC+0. 733 1. 7) ≤ 1. 267 0 → C 1. 85 Non-basic: + 0. 267 1. 7 = 2. 798 ← f. A CA-f. A ≤ 0 C 0. 789 2. 138 ü – OBJ (1. 833 C coefficient ranges≤ 0 → CC 1. 785 C– 0. 667 1. 7) CA - 2. 798 0 CA 2. 798 可 – 0. 183 CC + 0. 067 1. 7 ≤ 0 → CC 0. 622 VARIABLE CURRENT ALLOWABLE 調升量為 2. 798 – 1. 417 = 1. 38 0. 117 CC – 0. 133 1. 7 ≤ 0 → CC ≤ 1. 932 COEF INCREASE DECREASE A 1. 417000 1. 932 – 1. 379667 INFINITY 1. 85 – 1. 785 = 0. 065 B 1. 430000 = 0. 082. 248333 INFINITY C 1. 850000. 082857. 065636 D 2. 138000. 120333 INFINITY E 1. 700000. 180500. 081250 THE TABLEAU THE ROW (BASIS) A A BB C D EE SLK 2 ROW C D SLK 2 SLK 3 SLK 4 1 1 ART 00 ART 1. 417 1. 43 1. 85 2. 138 1. 7 00 00 2 2(1. 85) 1. 267 (1. 85)CC 1. 267. 2331. 000 1. 833. 000. 183 -. 117. 000 0 3 3(1. 7). 267 (1. 7)E E. 267. 733. 000 -. 667 1. 000 -. 067. 133. 000 0 4 4 SLK 4 -4. 4006. 900. 000 -8. 500. 000 -1. 150. 550 1. 000 2021/10/18 1817 512 512 3072. 000 3
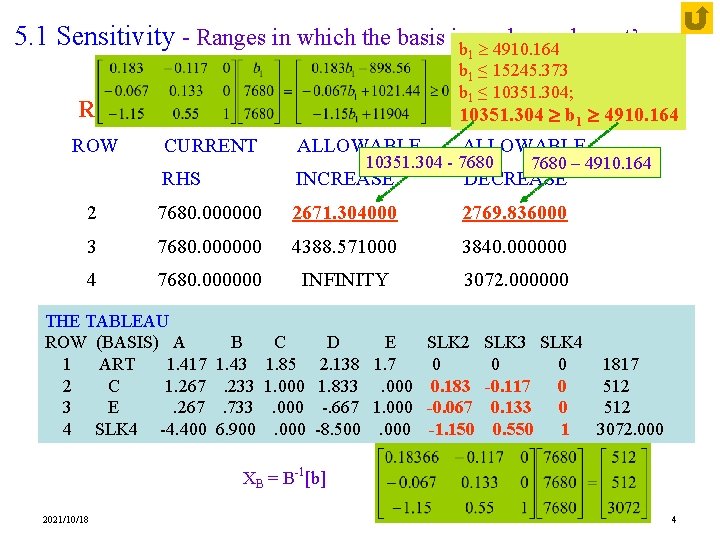
5. 1 Sensitivity - Ranges in which the basis isb unchanged: cont’ 4910. 164 1 b 1 ≤ 15245. 373 b 1 ≤ 10351. 304; Righthand side ranges ROW 10351. 304 b 1 4910. 164 CURRENT ALLOWABLE RHS INCREASE DECREASE 2 7680. 000000 2671. 304000 2769. 836000 3 7680. 000000 4388. 571000 3840. 000000 4 7680. 000000 INFINITY 3072. 000000 THE TABLEAU ROW (BASIS) A 1 ART 1. 417 2 C 1. 267 3 E. 267 4 SLK 4 -4. 400 B 1. 43. 233. 733 6. 900 10351. 304 - 7680 C 1. 85 1. 000 D E 2. 138 1. 7 1. 833. 000 -. 667 1. 000 -8. 500. 000 SLK 2 0 0. 183 -0. 067 -1. 150 7680 – 4910. 164 SLK 3 SLK 4 0 0 1817 -0. 117 0 512 0. 133 0 512 0. 550 1 3072. 000 XB = B-1[b] 2021/10/18 4

5. 2 Sensitivity of changes – under basic solutions keep invariant Obj Coef. Range: (Basic solution will not change) (i) Max 1. 417 A+1. 43 B+1. 85 C+. . . is changed to be Max 1. 417 A+1. 43 B+1. 86 C+. . . Then the objective value increases $0. 01 × 512 = $5. 12 and the new Z* = $1817 + $5. 12 = $1822. 12 Since 1. 86 -1. 85=0. 01< 0. 082857, the objective value will increase. (ii) Max 1. 417 A+1. 43 B+. . . is changed to be Max 1. 617 A+1. 43 B. . . , then the objective value increases $0 and the new objective value= $1817 (no change). Righthand Side Range: (Basic var. s will not change, but values for basic sol. s will change) Example: Increasing 100 units in resource 1 (so we have 7680+100 units in resource 1). Since 100 < 2671. 3042, we know that the basic variables are still C, E, and SLK 4. But the value for C will change, not 512. (of course Z* will change→ 1817+100*0. 226=1839. 6). resource 1’s shadow price 2021/10/18 5
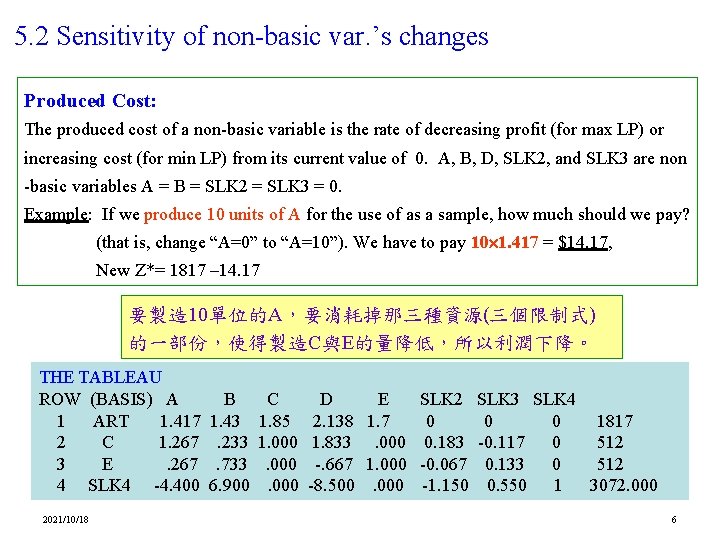
5. 2 Sensitivity of non-basic var. ’s changes Produced Cost: The produced cost of a non-basic variable is the rate of decreasing profit (for max LP) or increasing cost (for min LP) from its current value of 0. A, B, D, SLK 2, and SLK 3 are non -basic variables A = B = SLK 2 = SLK 3 = 0. Example: If we produce 10 units of A for the use of as a sample, how much should we pay? (that is, change “A=0” to “A=10”). We have to pay 10 1. 417 = $14. 17, New Z*= 1817 – 14. 17 要製造 10單位的A,要消耗掉那三種資源(三個限制式) 的一部份,使得製造C與E的量降低,所以利潤下降。 THE TABLEAU ROW (BASIS) A 1 ART 1. 417 2 C 1. 267 3 E. 267 4 SLK 4 -4. 400 2021/10/18 B 1. 43. 233. 733 6. 900 C 1. 85 1. 000 D E 2. 138 1. 7 1. 833. 000 -. 667 1. 000 -8. 500. 000 SLK 2 0 0. 183 -0. 067 -1. 150 SLK 3 SLK 4 0 0 1817 -0. 117 0 512 0. 133 0 512 0. 550 1 3072. 000 6
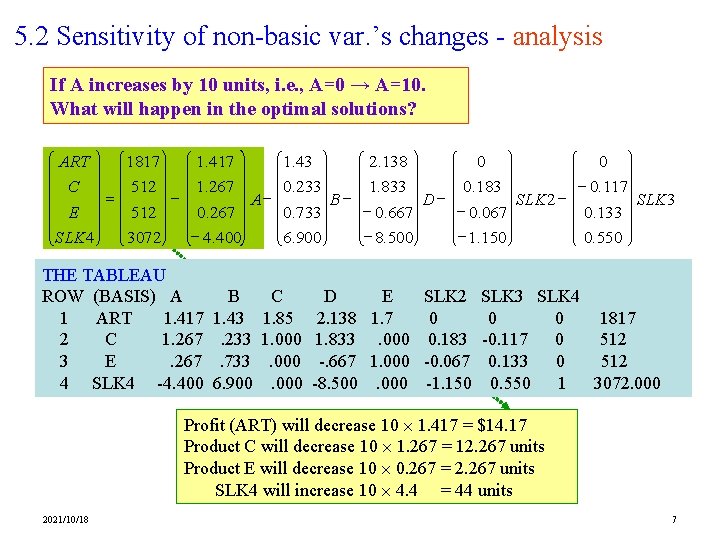
5. 2 Sensitivity of non-basic var. ’s changes - analysis If A increases by 10 units, i. e. , A=0 → A=10. What will happen in the optimal solutions? ART 1817 1. 417 C 512 1. 267 = AE 512 0. 267 - 4. 400 SLK 4 3072 THE TABLEAU ROW (BASIS) A 1 ART 1. 417 2 C 1. 267 3 E. 267 4 SLK 4 -4. 400 B 1. 43. 233. 733 6. 900 1. 43 0. 233 B 0. 733 6. 900 ART C C 1. 85 E 1. 0004 SLK 2. 138 0 0 - 0. 117 1. 833 0. 183 D SLK 2 SLK 3 - 0. 667 - 0. 067 0. 133 - 8. 500 - 1. 150 0. 550 1817 1. 417 D E SLK 2 SLK 3 SLK 4 512 1. 267 0 0 1817 =2. 138 1. 7 A 0 512. 000 0. 0. 183 267 -0. 117 0 1. 833 512 -. 667 512 30721. 000 - 4 -0. 067. 400 0. 133 0. 000 -8. 500. 000 -1. 150 0. 550 1 3072. 000 Profit (ART) will decrease 10 1. 417 = $14. 17 Product C will decrease 10 1. 267 = 12. 267 units Product E will decrease 10 0. 267 = 2. 267 units SLK 4 will increase 10 4. 4 = 44 units 2021/10/18 7

5. 2 Sensitivity of changes - cont’ (sensitivity analysis是allowable的就能change嗎?) Dual Price (或稱dual variable, that is, Y in dual LP) MIN 7680 Y 1+7680 Y 2+7680 Y 3 S. T. 12 Y 1 + 8 Y 2 + 5 Y 3 1. 417 7 Y 1 + 9 Y 2 +10 Y 3 1. 43 8 Y 1 + 4 Y 2 + 7 Y 3 1. 85 10 Y 1 + 3 Y 3 2. 183 7 Y 1 +11 Y 2 + 2 Y 3 1. 7 Y 1, Y 2, Y 3 0 Why Y 3* is 0 ? 因為沒有用完 MAX 1. 417 A + 1. 43 B + 1. 85 C + 2. 138 D + 1. 7 E SUBJECT TO 512 15 512 Resource 1: 2) 12 A + 7 B + 8 C + 10 D + 7 E <= 7680 Resource 2: 3) Resource 3: 4) 8 A +9 B+4 C + 11 E <= 7680 5 A + 10 B + 7 C + 3 D + 2 E <= 7680 If 240 units of new resource can be added into resources 1, 2 , or 3, and we know that it costs $0. 16667/per unit of new resource. (i) Should we add (buy) the new resource? Yes. ( 先確定加(買)入資源會不會賺?) See dual price 可加於 resource 1 (買入一個resource 1花$0. 16667,但可提高利 潤$0. 225833) See Righthand Side Ranges: Allowable increase for resource 1 = 2671. 304, Because 240<2671. 304119 不可加於 resource 2, 成本高過其marginal value。 結論: 資源可全收購,且全加於 resource 1 2021/10/18 8
- Slides: 8