5 Representations of the Symmetric Groups Sn 5




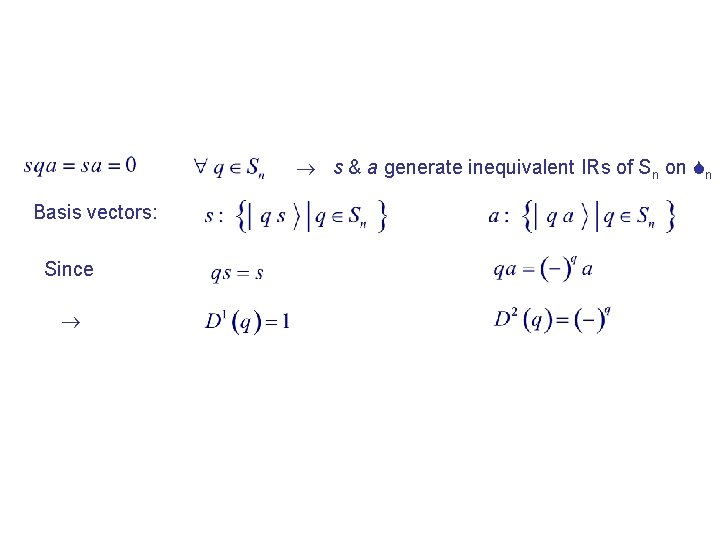















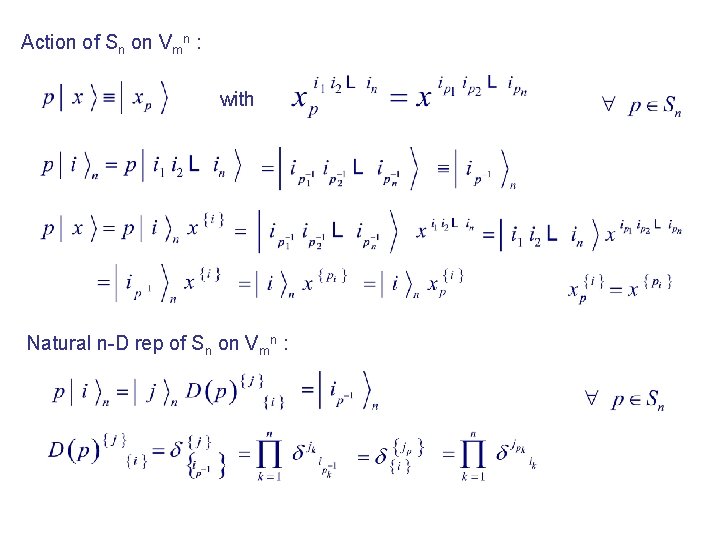
![Coming Attractions: • D[Gm] & D[Sn] are in general reducible. • D[Sn] can be Coming Attractions: • D[Gm] & D[Sn] are in general reducible. • D[Sn] can be](https://slidetodoc.com/presentation_image/525ec78ef1ac0bebc7f646784709a428/image-24.jpg)
![Lemma 5. 1: Gm & Sn are symmetry preserving on Vmn For both D[Gm] Lemma 5. 1: Gm & Sn are symmetry preserving on Vmn For both D[Gm]](https://slidetodoc.com/presentation_image/525ec78ef1ac0bebc7f646784709a428/image-25.jpg)














- Slides: 39

5. Representations of the Symmetric Groups Sn 5. 1 5. 2 5. 3 5. 4 5. 5 One-Dimensional Representations Partitions and Young Diagrams Symmetrizers and Anti-Symmetrizers of Young Tableaux Irreducible Representations of Sn Symmetry Classes of Tensors App III & IV

Importance of Sn: • Cayley's theorem: Every group of order n is isomorphic to a subgroup of Sn • Construction of IRs of classical groups, e. g. , GL(n), U(n), SU(n), etc • Identical particles Basic tools: Young diagrams, Young tableaux Symmetrizers, anti-symmetrizers, Irreducible symmetrizers ( Idempotents / Projections ) nth rank tensors on m-D space : Sn + GL(m)

5. 1. 1 -D Reps Every Sn has a non-trivial invariant subgroup, the alternating group, An = { All even permutations } Sn / A n C 2 Every Sn has two 1 -D reps: Identity rep 1 : 2 : D(p) = 1 D(p) = (–) p p

Theorem 5. 1: Symmetrizer & antisymmetrizer are essentially idempotent & primitive Proof: s is essentially idempotent & primitive a is essentially idempotent & primitive
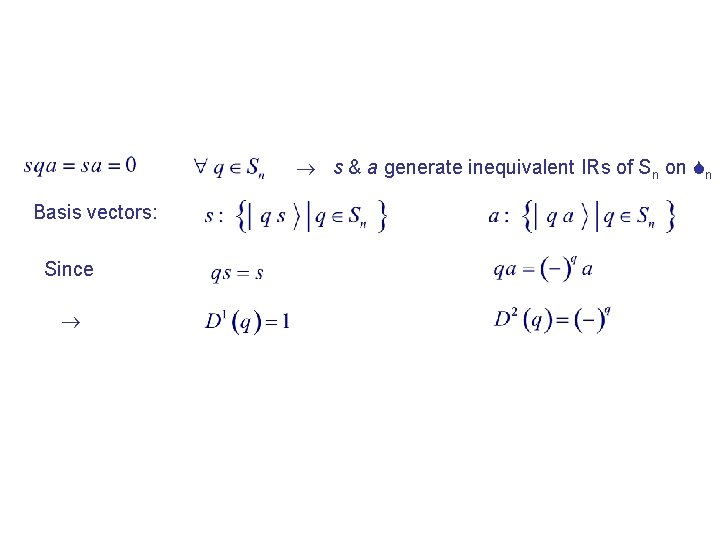
s & a generate inequivalent IRs of Sn on Sn Basis vectors: Since

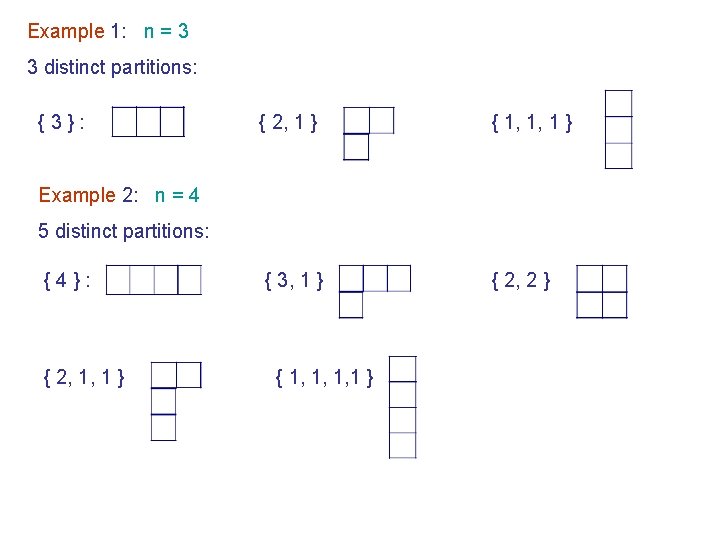
5. 2. Partitions and Young Diagrams Definition 5. 1: Partition of n , Young Diagram A partition of integer n is an ordered sequence of integers such that & 2 partitions & are equal if if the 1 st non-zero member in sequence is positive negative A partition is represented graphically by a Young diagram of n squares arranged in r rows, the jth of which contains j squares

Example 1: n = 3 3 distinct partitions: {3}: { 2, 1 } { 1, 1, 1 } { 3, 1 } { 2, 2 } Example 2: n = 4 5 distinct partitions: {4}: { 2, 1, 1 } { 1, 1, 1, 1 }

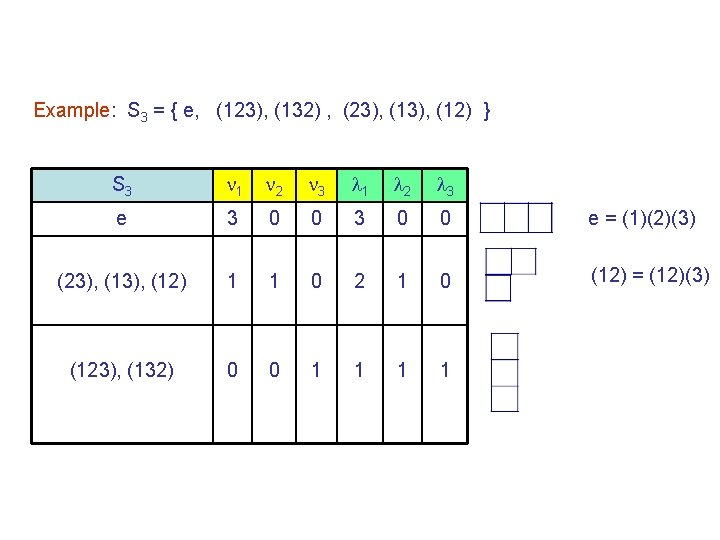
Partition of n ~ Classes of Sn Let there be j j-cycles in an element in a class of Sn Then ( most k = 0 ) is a partition of n Theorem 5. 2: Number of distinct Young diagram for n = Number of classes in Sn = Number of inequivalent IRs in Sn

Example: S 3 = { e, (123), (132) , (23), (12) } S 3 1 2 3 e 3 0 0 e = (1)(2)(3) (23), (12) 1 1 0 2 1 0 (12) = (12)(3) (123), (132) 0 0 1 1

Definition 5. 2: Young Tableau, Normal Tableau, Standard Tableau A tableau is a diagram filled with a distinct number (1, …, n) in each square. (i) Young Tableau: Numbers filled with no particular order (ii) Normal Tableau : Numbers filled consecutively from left to right & top to bottom (iii) Standard Tableau p : Numbers ordered from left to right in each row & top to bottom in each column Example: S 4 Standard tableaux p Normal tableaux p = (3, 4) p = (2, 3)

5. 3. Symmetrizers & Anti-Symmetrizers of Young Tableaux Definition 5. 3: Horizontal and Vertical Permutations Let p be any tableau. A horizontal ( vertical ) permutation h p ( v p ) is a permutation that does not exchange numbers between different rows (columns). Each cycle in h p ( v p ) must contain numbers that appear in the same row (column). Definition 5. 4: Symmetrizer, Anti-symmetrizer, Irreducible Symmetrizer: Anti-symmetrizer: Irreducible symmetrizer:

Example: S 3 Observations: 1) { h p } and { v p } are each a subgroup of S 3. 2) s and a are total (anti-)symmetrizers of these subgroups. Also: ( Rearrangement theorem used on subgroup { h } ) s and a are essentially idempotent. 3) e are primitive idempotents : 4) 5. 3. Cases e 1 & e 3 are obvious. For case e 2, see Problem

4) { e } generates a set of inequivalent IRs of S 3. 5) Cases e 1 & e 3 are obvious. 6) Case e 2 is proved by showing that 7) S 3. { p e 2 p S 3 } spans a 2–D subspace (left ideal) of QED

5) Similarly e 2(23) also generate a 2 -D IR but it is equivalent to that from e 2. 6) The left ideal is however distinct from that of e 2. It is spanned by & 6) The group algebra is a direct sum of the 4 left ideals generated by the standard tableaux e 1 , e 2(23) and e 3. 7) The identity can be decomposed as DR is fully reduced by the e 's of the standard tableaux

Summary of the lemmas proved in Appendix IV: Lemma IV. 1: x p = p x p– 1 Lemma IV. 2: For a given tableau { h } & { v } are each a subgroup of Sn. Given and p Sn. Lemma IV. 3: Lemma IV. 4: at least 2 numbers in one row of which appear in the same column of p. Given and p Sn ( ~ denotes transpositions )

Lemma IV. 5: Given and r G. of Lemma IV. 6: Given 2 distinct diagrams > , Lemma IV. 7: The linear group transformations on Vmn , spans the space K of all symmetry-preserving linear transformations.

5. 4. Irreducible Representations of Sn ( Superscripts p in p, s p…, are omitted ) Theorem 5. 3: For a given Young tableau : and Proof: ( e is essentially idempotent ) By lemma IV. 2 : By lemma IV. 5 : where of of Since e s and e a while (–)e = 1, we have αe 0 QED

Theorem 5. 4: e IR e is a primitive idempotent. It generates an IR of Sn on Sn. Proof: ( Theorem 5. 3 ) By theorem III. 3, e is a primitive idempotent. Theorem 5. 5: QED Equivalent IRs generated by e and e p , p Sn, are equivalent Proof: ( Theorem 5. 3 ) Proof is completed by theorem III. 4.

Theorem 5. 6: Inequivalent IRs e & e generate inequivalent IRs if ( different Young diagrams ) Proof: Let > & p Sn. Lemma IV. 6 QED by theorem III. 4 Example: e 1, e 2, e 3 of S 3 generate inequivalent IRs Corollary: Proof: Case > is proved in lemma IV. 6. Case < is left as exercise.

Theorem 5. 7: IRs of Sn { e } of all normal tableaux generate all inequivalent IRs of Sn. Proof: 1. Number of inequivalent IRs = Number of Young diagrams ( theorem 5. 2 ) 2. Each normal diagram begets an e 3. Every e generates an inequivalent IR ( theorem 5. 6 ) Theorem 5. 8: Decomposition of DR 1. Left ideals L a generated by e a 's associated with distinct standard tableaux are linearly independent. 2. Proof: See W. Miller, "Symmetry Groups & Their Applications", Academic Press (1972)

5. 5. Symmetry Classes of Tensors Let Vm be an m-D vector space with basis { | i , i = 1, …, m } { g } be all invertible linear transformations on Vm { g } = GL(m, C) = General linear group = Gm Natural m-D rep of Gm on Vm : g i j = ( i, j ) element of an invertible m m matrix Definition 5. 5: Tensor Space Vmn

Natural basis of Vmn : = tensor components of x Natural (nm)-D rep of Gm on Vmn :
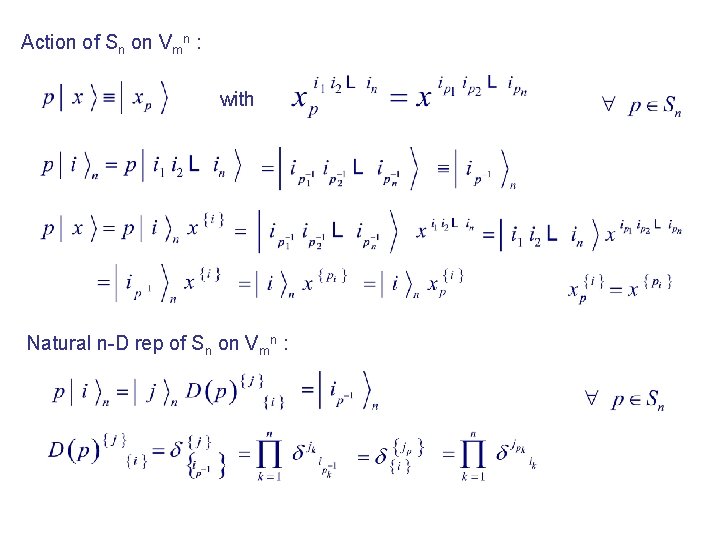
Action of Sn on Vmn : with Natural n-D rep of Sn on Vmn :
![Coming Attractions DGm DSn are in general reducible DSn can be Coming Attractions: • D[Gm] & D[Sn] are in general reducible. • D[Sn] can be](https://slidetodoc.com/presentation_image/525ec78ef1ac0bebc7f646784709a428/image-24.jpg)
Coming Attractions: • D[Gm] & D[Sn] are in general reducible. • D[Sn] can be decomposed using e 's of Sn. • Since p & g commutes, Gm can be decomposed using e 's of Sn from reduction of Vmn.
![Lemma 5 1 Gm Sn are symmetry preserving on Vmn For both DGm Lemma 5. 1: Gm & Sn are symmetry preserving on Vmn For both D[Gm]](https://slidetodoc.com/presentation_image/525ec78ef1ac0bebc7f646784709a428/image-25.jpg)
Lemma 5. 1: Gm & Sn are symmetry preserving on Vmn For both D[Gm] & D[Sn] : where Proof: Follows directly from the explicit form of D[Gm] & D[Sn]. Theorem 5. 9: pg=gp g Gm & p Sn QED

Example 1: Basis of V 22 : S 2 = { e, (12) } V 2 2

Preview: In the decomposition of Vmn using e p, one gets 1. An irreducible invariant subspace wrt Sn: 2. An irreducible invariant subspace wrt Gm: 3. The decomposed Vmn has basis | , , a , where 4. denotes a symmetry class / Young diagram, 5. labels the irreducible invariant subspaces under Sn, and 6. a labels the irreducible invariant subspaces under Gm

Definition 5. 6: Tensors of Symmetry p & Tensors of Symmetry Class Given Young tableau p : Tensors of Symmetry p = Given Young diagram labelled : Tensors of Symmetry Class =

Theorem 5. 10: Let ( α fixed ) 1. T (α) is an irreducible invariant subspace wrt Sn. 2. T (α) realization of Sn on T (α) coincides 3. Proof of 1: with IRs generated by e on Sn. For some QED Proof of 2: Let { ri e } be a basis of L , then { ri e | } is a basis for T ( ). If then on Sn on T ( ) QED

= s = total symmetrizer Ls is 1 -D Ts( ) = totally symmetric tensors Realization of Sn on Ts( ) is the identity representation D 1(p) = 1 p

Example 2: V 2 3 ( Symmetry class s ) 4 distinct totally symmetric tensors ( = s ) can be generated: 1. Ts(1) 2. Ts(2) 3. Ts(3) 4. Ts(4) Each Ts( ) is invariant under S 3 All 4 | s, j, 1 together span a subspace Ts invariant under G 2 There is no symmetry class a for V 23 Problem 5. 6: Symmetry class a exists only in Vmn with m n.

Example 3: Totally anti-symmetric tensor 1 & only 1 totally anti-symmetric tensor in Vnn. n= 2: n= 3: Example 4: if ( i j k ) is V m 2 , m 2 m ( m+1) / 2 distinct totally symmetric tensors: m ( m– 1) / 2 distinct totally anti-symmetric tensors: permutations of (123)

Example 5: V 2 3 mixed symmetry = m 2 independent irreducible invariant subspaces of tensors with mixed symmetry can be generated. Normal tableau Standard tableau 1. | m, 1, 1 & | m, 1, 2 span the 2 -D subspace Tm(1), invariant under S 3

2. | m, 2, 1 & | m, 2, 2 span the 2 -D subspace Tm(2), invariant under S 3 Tm (1) is invariant under G 2. Ditto

Summary: The 8 -D V 23 is decomposed into 4 1 -D class s & 2 2 -D class m irreducible subspaces invariant under S 3 Basis | , , * for each T ( ) is obtained by applying all standard tableaux p to a single | The 8 -D V 23 is decomposed into 1 4 -D class s & 2 2 -D class m irreducible subspaces invariant under G 2 Basis | , *, p for each T (p) is obtained by applying each standard tableaux p to all |

T ( ) = span { e p | } is invariant under Sn Theorem 5. 11: 1. Either or 2. ( disjoint ) if (different symmetries ) Proof of 1: Either or T ( ) & T ( ) has at least 1 non-zero element in common, i. e. , Proof of 2: is also invariant under Sn. Since T ( ) & T ( ) are irreducible & QED

Observations: Theorem 5. 11 implies Each T ( ) is invariant under Sn Basis | , , * for each T ( ) is obtained by applying e p of all standard tableaux p to a single | It is permissible to the same D (Sn) for all 's : a, b = 1, …, dim T ( ) = Number of standard tableaux * of symmetry

Theorem 5. 12: is invariant under Gm IR of Gm on T (a) satisfies Reminder: | , *, a is obtained by applying e a of standard a to all | Proof: Since theorem 5. 9 Schur's lemma: QED

Theorem 5. 13: IRs of Gm Reps of Gm on T (a) of Vmn are IRs. Reminder: | , *, a is obtained by applying e a of standard a to all | Outline of Proof: For complete proof, see W. Miller, "Symmetry Groups & Their Applications", Academic Press (72) Rationale: Since Gm is the largest group that commutes with Sn on T (a) of Vmn, the operators D(g) should be complete & hence irreducible. Let A be a linear operator on T (a) : Since x & y belong to the same symmetry class , A must be symmetry preserving, i. e. , Lemma 5. 1 states that g Gm on Vmn are symmetry preserving. Lemma IV. 7 A is a linear combination of D(g) is irreducible