5 Rates of Change and Particle Motion RATE

5. Rates of Change and Particle Motion

RATE OF CHANGE The derivative represents the instantaneous change of a function. f(x) may represent a particle’s position, but it can also represent ANY quantity such as area of a circle or outdoor temperature, or amount of rainfall, or number of people infected with a disease, etc. This is the true power of the derivative, it gives us a way to talk about how fast ANYTHING is changing at a single moment in time.

EXAMPLE 1 The temperature T in degrees Fahrenheit of a cold yam placed in a hot oven is given by T=f(t), where t is the time in minutes since the yam was put into the oven. A. What is the practical meaning of f(20)=255? B. What is the sign of f’(t)? Why? C. What are the units of f’(20)? D. What is the practical meaning of f’(20)=2?

EXAMPLE 2 An ice cream company knows the cost, C (in dollars), to produce q quarts of cookie dough ice cream is a function of q, so C = f(q). A. If f(200)=70, what are the units of the 200? What are units of the 70? Explain clearly what this equation means. B. If f’(200)=-3, what are the units of the 200? What are units of the -3? Explain clearly what this equation means.

INSTANTANEOUS RATE OF CHANGE The word instantaneous is often used even when the function does not involve time. In addition, the word instantaneous is often omitted. When we say “rate of change”, we mean “instantaneous rate of change”

EXAMPLE 3 The area of a circle is increasing. How fast is the area of the circle changing with respect to the radius when the radius is 5 inches and when the radius is 10 inches? How fast is the circumference changing at these times?

MOTION There is perhaps no more important type of rate of change than that of motion. After all, this was Newton’s motivation for inventing calculus to begin with. The next slide gives some summary information about motion.

MOTION The derivative (slope) of position is velocity The derivative (slope) of velocity is acceleration Displacement is where you are when you end – where you are when you start ( s(b) – s(a)) Distance traveled is the sum of the absolute values of displacement between resting position Average velocity is displacement/time (slope of secant line) Instantaneous velocity is the derivative of position (slope of the tangent line) Velocity tells the direction a particle is moving (positive is to the right, negative is to the left) When velocity changes sign, the particle changes direction When velocity is 0, a particle is stopped (or at rest) Speed is the absolute value of velocity Speed is increasing if velocity and acceleration have the same sign (you see this on a graph as moving away from the x-axis) Speed is decreasing if velocity and acceleration have different signs (you see this on a graph as moving toward the x-axis) If acceleration is positive, velocity is increasing If acceleration is negative, velocity is decreasing

EXAMPLE 4

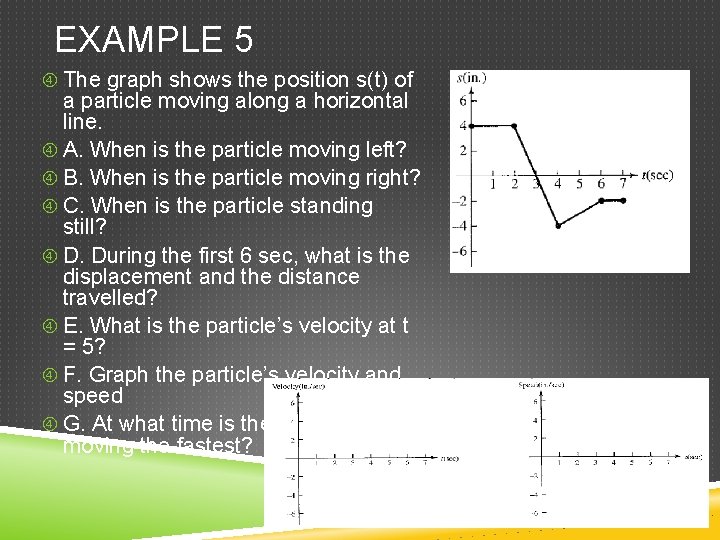
EXAMPLE 5 The graph shows the position s(t) of a particle moving along a horizontal line. A. When is the particle moving left? B. When is the particle moving right? C. When is the particle standing still? D. During the first 6 sec, what is the displacement and the distance travelled? E. What is the particle’s velocity at t = 5? F. Graph the particle’s velocity and speed G. At what time is the particle moving the fastest?

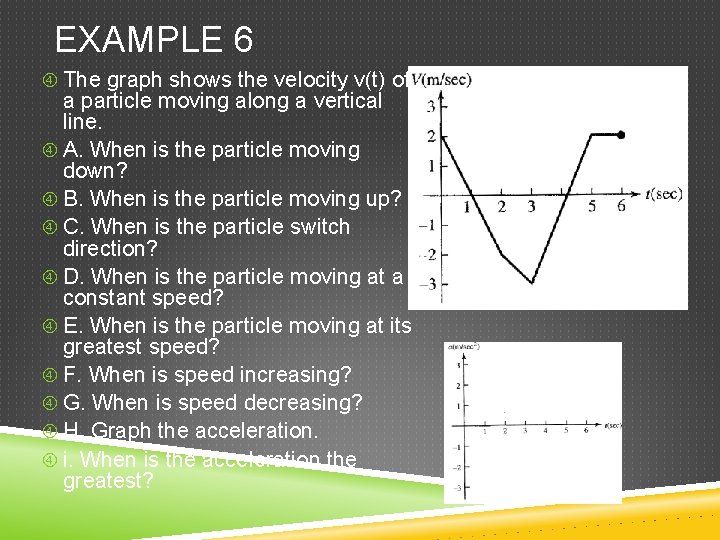
EXAMPLE 6 The graph shows the velocity v(t) of a particle moving along a vertical line. A. When is the particle moving down? B. When is the particle moving up? C. When is the particle switch direction? D. When is the particle moving at a constant speed? E. When is the particle moving at its greatest speed? F. When is speed increasing? G. When is speed decreasing? H. Graph the acceleration. i. When is the acceleration the greatest?

EXAMPLE 7 The values of the coordinate s of a moving body along a line for various values of t are given below. Estimate the velocity at A. t = 0. 5 s b. t = 2. 7 s c. t = 3. 5 s

MARGINAL COST Marginal cost is the extra cost of producing one more unit = C’(x) Marginal revenue is the extra money brought in from selling one more unit Marginal profit is the extra profit from making and selling one more unit Profit = revenue – cost Average cost = C(x)/x dollars per unit

EXAMPLE 8