5 Random Variables Lesson 5 4 Analyzing Binomial

5 Random Variables Lesson 5. 4 Analyzing Binomial Random Variables Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Analyzing Binomial Random Variables Learning Targets After this lesson, you should be able to: ü Calculate and interpret the mean and standard deviation of a binomial distribution. ü Find probabilities involving several values of a binomial random variable. ü Use technology to calculate cumulative binomial probabilities. Statistics and Probability with Applications, 3 rd Edition 2

Analyzing Binomial Random Variables To calculate the mean of a discrete random variable X, we use the formula µX = E(X) = x 1 p 1 + x 2 p 2 + x 3 p 3 +. . . Calculating the Mean of a Binomial Random Variable If a count X of successes has a binomial distribution with number of trials n and probability of success p, the mean of X is µX = np Statistics and Probability with Applications, 3 rd Edition 3

Analyzing Binomial Random Variables To calculate the standard deviation of a discrete random variable X, we use the formula Calculating the Standard Deviation of a Binomial Random Variable If a count X of successes has a binomial distribution with number of trials n and probability of success p, the standard deviation of X is Caution! Remember that these formulas for the mean and standard deviation work only for binomial distributions. Statistics and Probability with Applications, 3 rd Edition 4

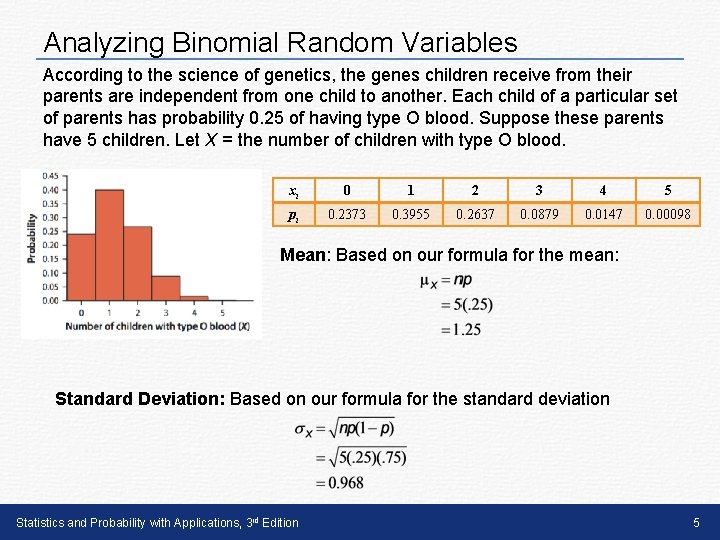
Analyzing Binomial Random Variables According to the science of genetics, the genes children receive from their parents are independent from one child to another. Each child of a particular set of parents has probability 0. 25 of having type O blood. Suppose these parents have 5 children. Let X = the number of children with type O blood. xi 0 1 2 3 4 5 pi 0. 2373 0. 3955 0. 2637 0. 0879 0. 0147 0. 00098 Mean: Based on our formula for the mean: Standard Deviation: Based on our formula for the standard deviation Statistics and Probability with Applications, 3 rd Edition 5

Analyzing Binomial Random Variables According to the science of genetics, the genes children receive from their parents are independent from one child to another. Each child of a particular set of parents has probability 0. 25 of having type O blood. Suppose these parents have 5 children. Let X = the number of children with type O blood. xi 0 1 2 3 4 5 pi 0. 2373 0. 3955 0. 2637 0. 0879 0. 0147 0. 00098 What’s the probability that at most 1 of the children has type O blood? In symbols, it’s P(X ≤ 1). We can compute this cumulative binomial probability using the fact that P(X ≤ 1) = P(X=0) + P(X=1) = 0. 23730 + 0. 39551 = 0. 63281 What if we want to find the probability that at least 2 of the couple’s 5 children have type O blood? In symbols, that’s P(X ≥ 2). We could compute this probability using the fact that P(X ≥ 2) = P(X=2) + P(X=3) + P(X=4) + P(X=5) = 0. 26367 + 0. 08789 + 0. 01465 + 0. 00098 = 0. 36719 Statistics and Probability with Applications, 3 rd Edition 6

LESSON APP 5. 4 Free lunch? A local fast-food restaurant is running a “Draw a three, get it free” lunch promotion. After each customer orders, a touch-screen display shows the message, “Press here to win a free lunch. ” A computer program then simulates one card being drawn at random from a standard deck of playing cards. If the chosen card is a 3, the customer’s order is free. (Note that the probability of drawing a 3 from a standard deck of playing cards is 4/52. ) Otherwise, the customer must pay the bill. Suppose that 250 customers place lunch orders on the first day of the promotion. Let X = the number of people who win a free lunch. Statistics and Probability with Applications, 3 rd Edition 7

LESSON APP 5. 4 1. 2. 3. 4. Free lunch? Explain why X is a binomial random variable. Find the mean of X. Interpret this value in context. Find the standard deviation of X. Interpret this value in context. One of the customers is surprised when only 10 people win a free lunch. Should the customer be surprised? Find the probability that 10 or fewer people win a free lunch by chance alone and use this result to support your answer. Statistics and Probability with Applications, 3 rd Edition 8

Analyzing Binomial Random Variables Learning Targets After this lesson, you should be able to: ü Calculate and interpret the mean and standard deviation of a binomial distribution. ü Find probabilities involving several values of a binomial random variable. ü Use technology to calculate cumulative binomial probabilities. Statistics and Probability with Applications, 3 rd Edition 9