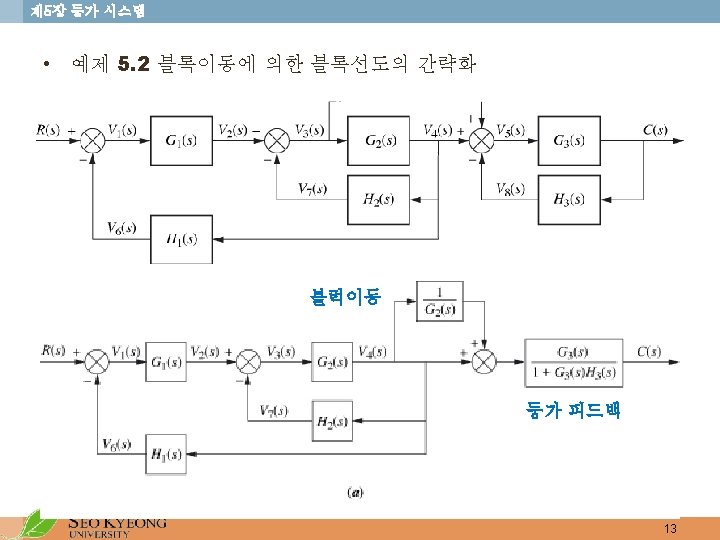
5 Parallel Form Block diagram Signal flow graph

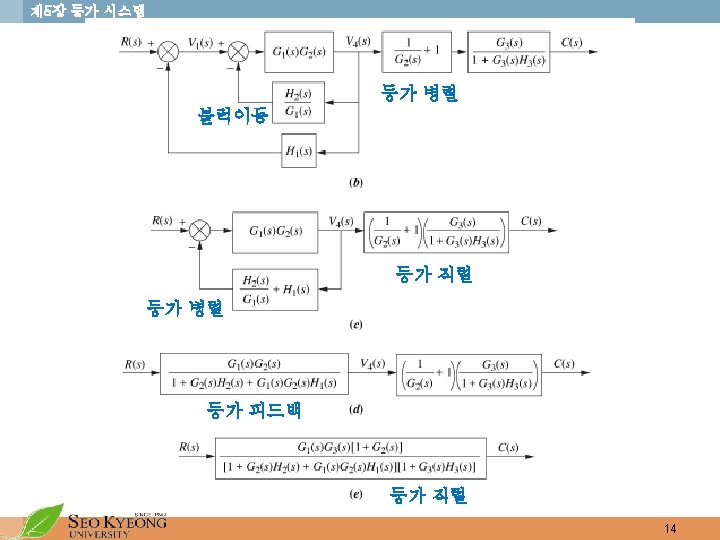
제 5장 등가 시스템 • 병렬형 (Parallel Form) • Block diagram • Signal flow graph 7

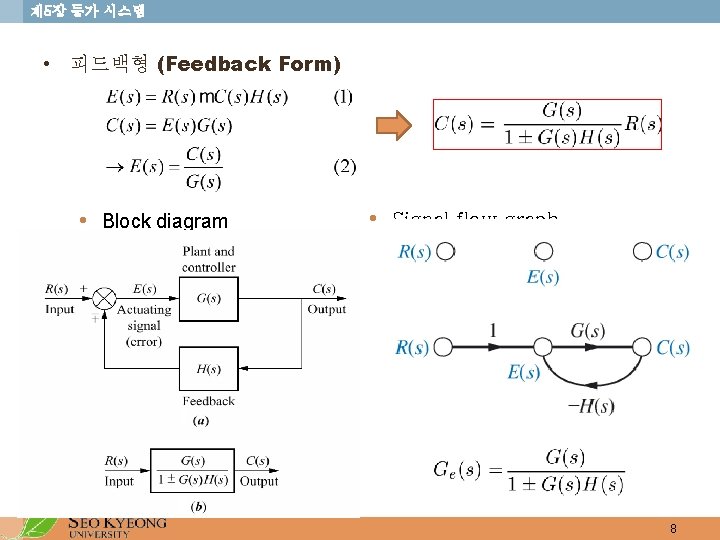
제 5장 등가 시스템 • 피드백형 (Feedback Form) • Block diagram • Signal flow graph 8

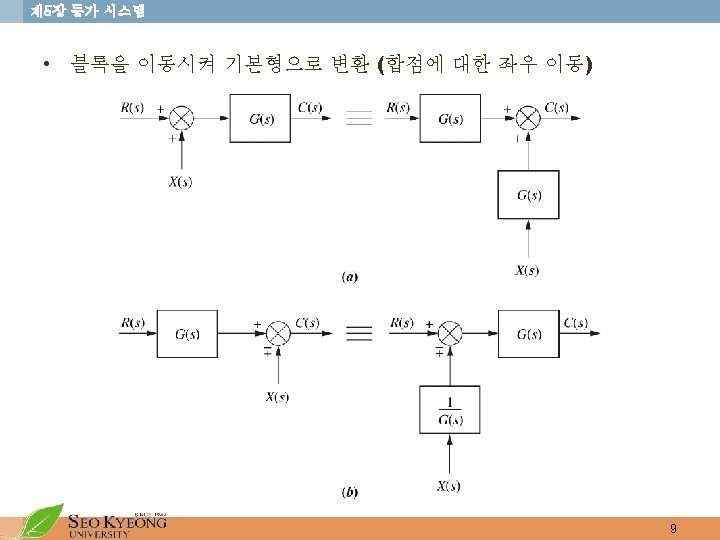
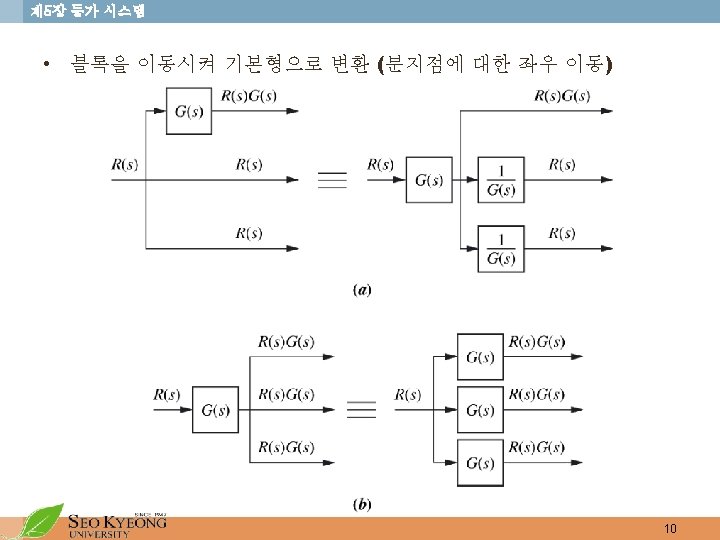
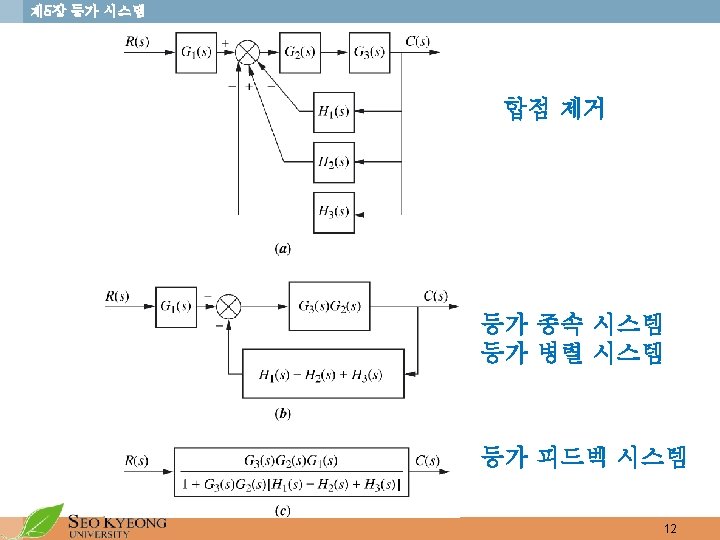
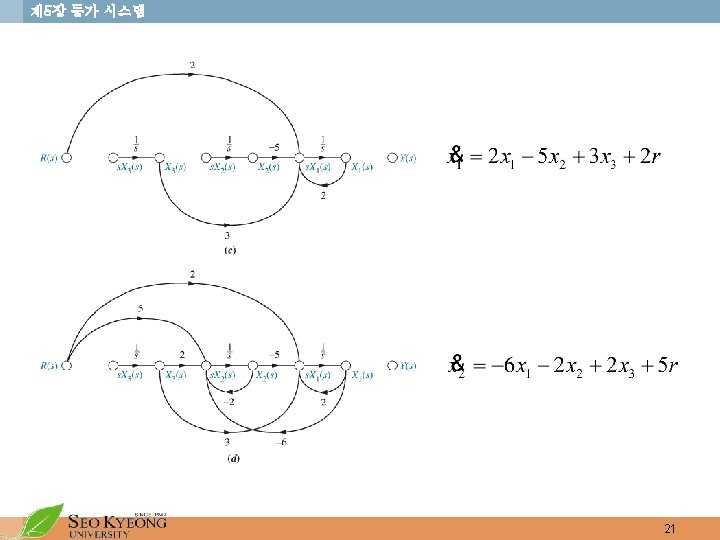
제 5장 등가 시스템 • Mason’s Rule for reduction of Signal Flow Graph • k = number of forward paths • Tk = the i th forward path gain • (individual loop gains) (nontouching loop gains taken two at a time) (nontouching loop gains taken three at a time) (nontouching loop gains taken four at a time) • (loop gains not touching the i th forward path)

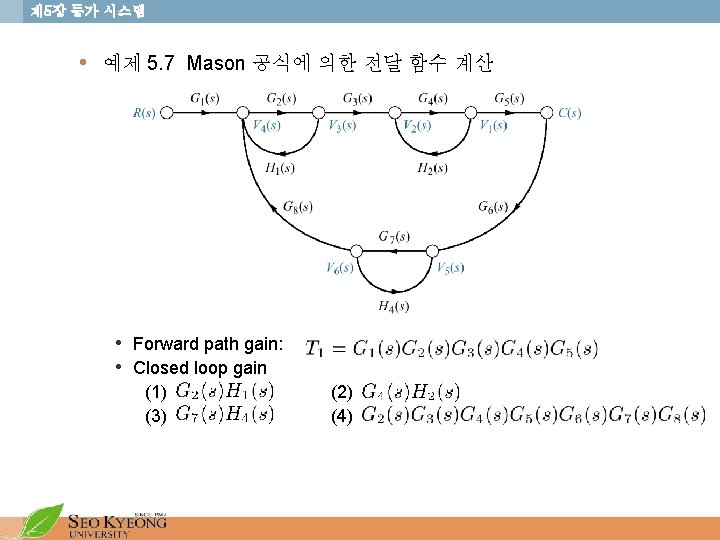
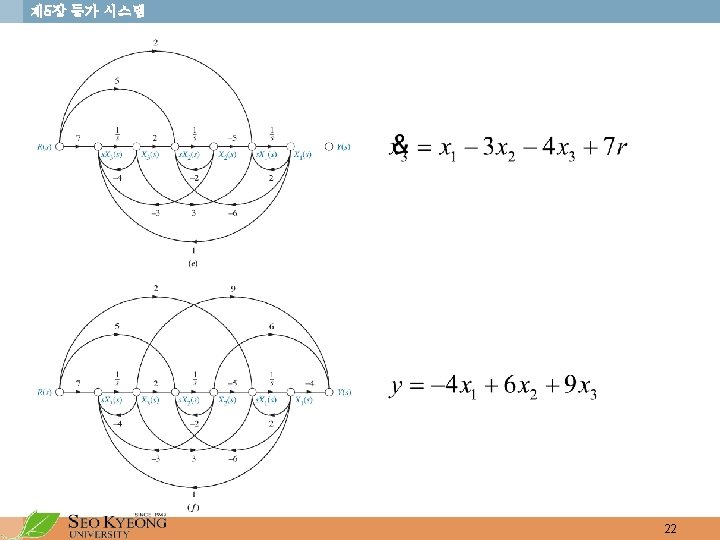
제 5장 등가 시스템 • Nontouching loops taken two at a time (5) loop (1) and loop (2): (6) loop (1) and loop (3): (7) loop (2) and loop (3): • Nontouching loops taken three at a time (8) loops (1), (2), (3): • Now, • Portion of not touching the forward path • Hence, 19

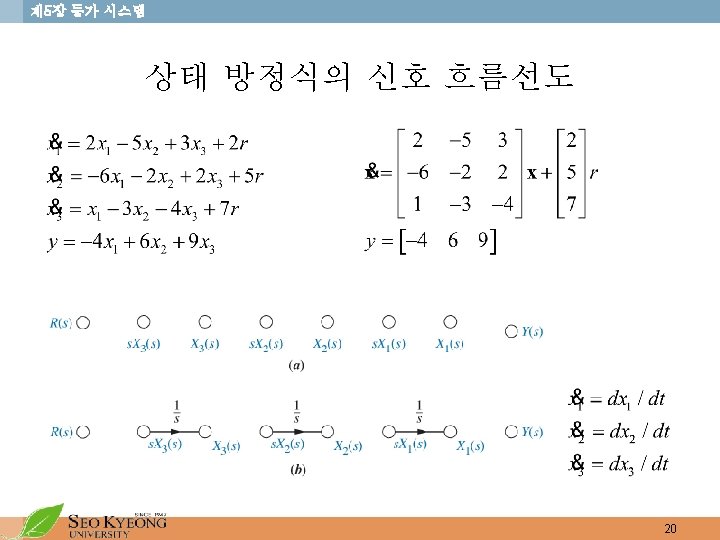
제 5장 등가 시스템 상태 공간에서의 다른 표현 • 위상변수형 (Phase-variable (canonical) form) • The system matrix A has the coefficients of the system’s characteristic polynomial along the last row. 23

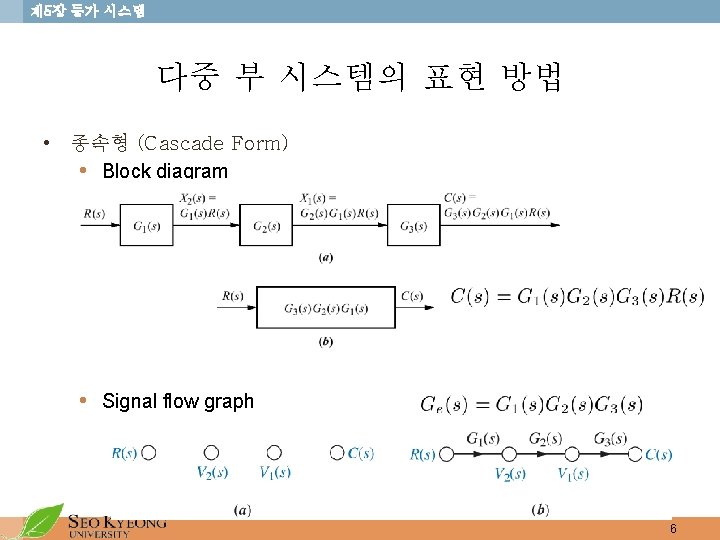
제 5장 등가 시스템 • 종속형 (Cascade form) • Each first-order block is of the form • Cross-multiplying • Taking the ILT, 24

제 5장 등가 시스템 • Representation of the system • The system matrix A has the poles along the diagonal and the terms relative to the internal system itself. 25

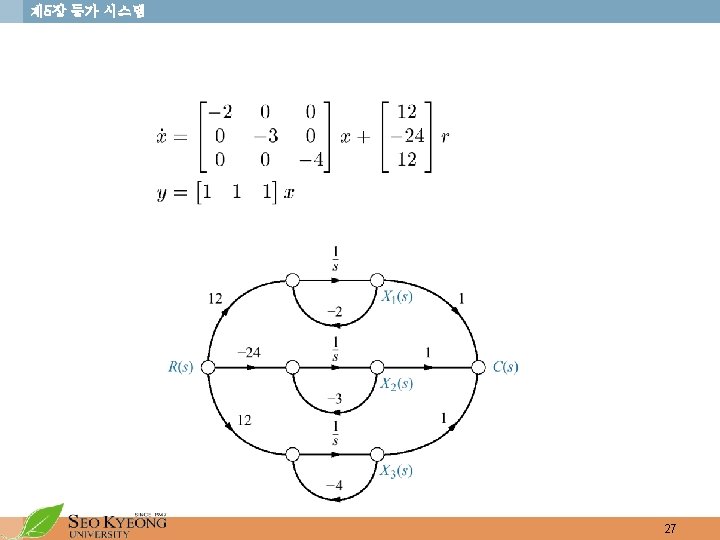
제 5장 등가 시스템 • 병렬형 (Parallel form) • First-order pole : If no system pole is a repeated root, A matrix becomes purely diagonal by PFE. • Representation of the system 26

제 5장 등가 시스템 • Multiple-order poles (repeated roots) • By PFE • Representation of the system 28

제 5장 등가 시스템 • A matrix is called the “Jordan Canonical Form” • Not purely diagonal but the system poles along the diagonal. 29

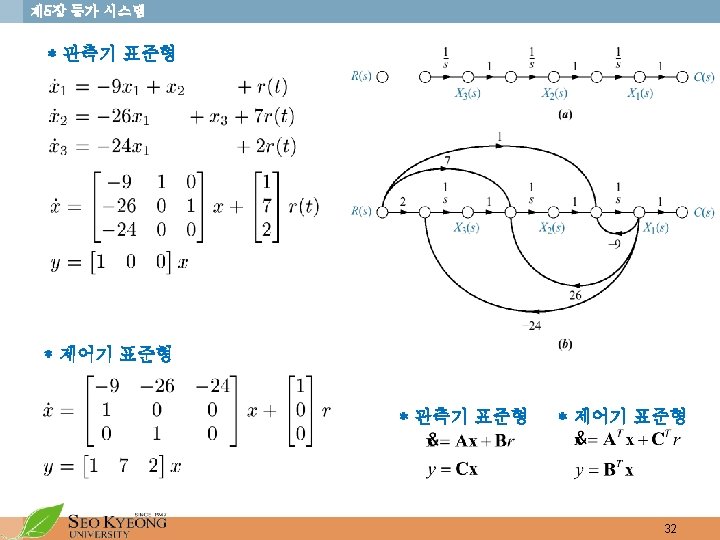
제 5장 등가 시스템 • 제어기 표준형 (Controller canonical form) • This form is obtained from the phase-variable form simply by ordering the phase-variable in the reverse order Figure 5. 27 a. phase-variable form b. controller canonical form 30

제 5장 등가 시스템 • 관측기 표준형 (Observer Canonical Form) • This is dual with the phase-variable form. • Divide by • Cross multiplying yields 31

제 5장 등가 시스템 유사변환 (Similarity Transform) • 전달함수는 같지만 상태 변수가 다른 시스템으로 표현 and are orthogonal; (linearly independent basis vector) 34