5 Overview Energy and the Joule Unit Energy

5 Overview • • • Energy and the Joule Unit. Energy transformation. Energy storage. Power and Watt Unit. Homework: 2, 6, 9, 11, 13, 15, 27, 33, 37, 45, 49, 53, 75, 77, 79, 81, 85, 101. 1

Energy and Transformation • chemical fuel energy vehicle motion • electric energy turning mixer, drill, etc. • wind turbine electrical energy turn mixer 2

definitions • Energy: The work that a physical system is capable of doing in changing from its actual state to a specified reference state … (American Heritage Dictionary) • Energy: The capacity to do work. (Physics) • What is Work? 3

Work • Work is force x distance. • energy required • Less stored energy is available after productive work is done. 4

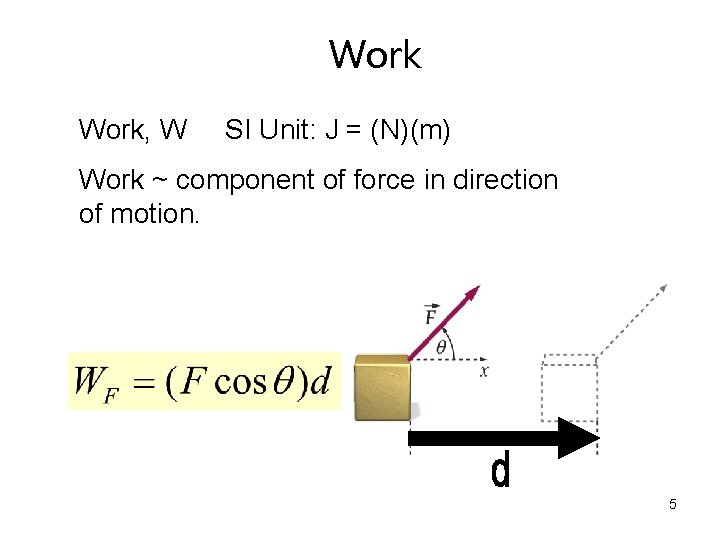
Work, W SI Unit: J = (N)(m) Work ~ component of force in direction of motion. 5

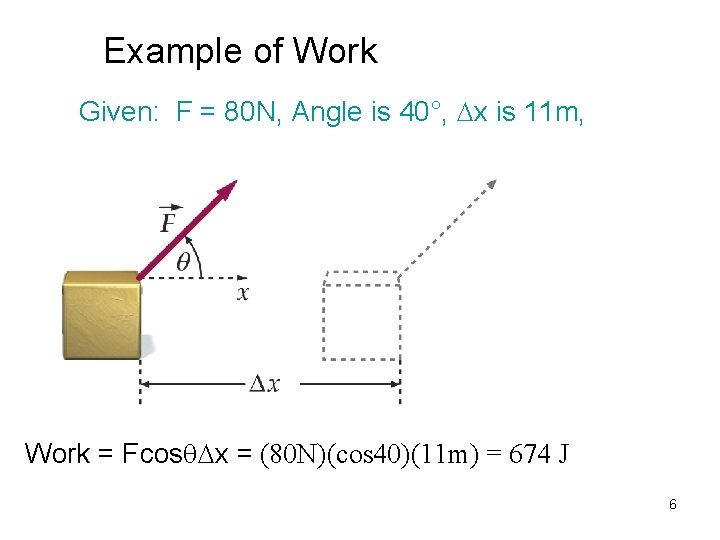
Example of Work Given: F = 80 N, Angle is 40°, Dx is 11 m, Work = Fcosq. Dx = (80 N)(cos 40)(11 m) = 674 J 6

Energy • Positional (Potential), e. g. compressed spring • Motional (Kinetic), e. g. moving car 7

Energy • Kinetic, K: energy of motion K = ½mv 2. • Ex: 2000 kg car moving at 10 m/s has kinetic energy of 100, 000 J. • Potential, U: stored energy • Ex: 1 gallon of gasoline > 100, 000 J. 8

Work-Energy Theorem: The net work done on an object is equal to its change in Kinetic Energy. Ex. Net work = 250 J. If m = 20 kg, vo = 0, Then final speed is 5 m/s: 250 = ½(20)52 – 0. 9

Example • A 20 kg mass is moving at 5 m/s. 250 J of work (net) are done on it. What is its final speed? 10

• A 20 kg block slides across a floor. The frictional force on it is 50 N. How much work is done on the block by friction in moving 3 m? • If its initial speed was 5 m/s, what is its speed after moving 3 m? 11

• A 20 kg block is pushed with 75 N of force. The frictional force on it is 50 N. How much net work is done on the block in moving 3 m? • If its initial speed was 5 m/s, what is its speed after moving 3 m? 12

• How much work does a force perpendicular to an objects displacement do? • Answer: Zero. The angle between F and displacement is 90, cos 90 = 0. 13

Some Potential Energies • • Spring: Usp. Gravitational: Ug Thermal: Uth Chemical, Nuclear • first three used in this class 14

Springs • Fsp = -kx, Usp = ½kx 2. • k = “spring constant” in N/m and x is the change in length of the spring. • Ex: A 100 N/m spring is compressed 0. 2 m. It exerts (100 N/m)(0. 2 m) = 20 N of force. It stores ½(100 N/m)(0. 2 m)2 = 2 J of energy. 15

Gravity • Fg = mg, Ug = mgy • Ex: 2 kg weighs (2 kg)(9. 8 N/kg) = 19. 6 N. 3 m above floor Ug = (2 kg)(9. 8 N/kg)(3 m) = 48. 8 J. 16

Conservation of Energy • Individual energy levels change. • Net energy is constant. • Change in energy is called “work” 17

Energy Conservation • Total Energy E = sum of all energies • E = SK + SU • example: • t = 0: K = • later: 0 J U = 4000 J K = 3000 J U = 1000 J 18

19

Conservation of Energy Example: Falling Ball KE increases U (gravitational) decreases E = K + Ug = constant 20

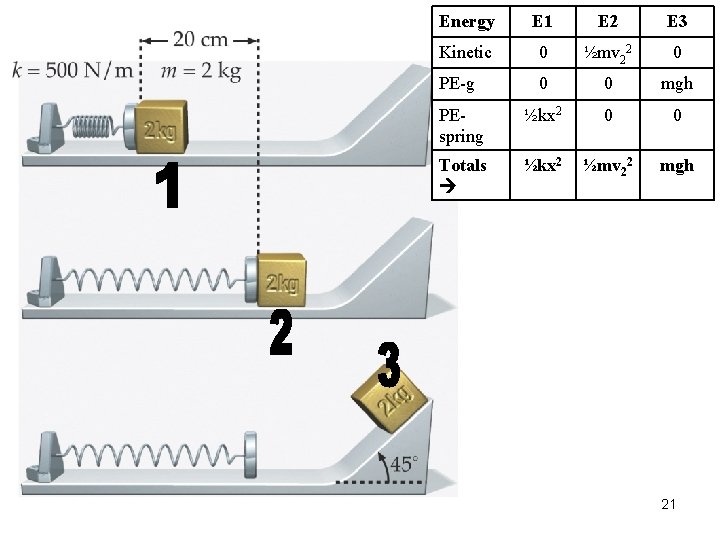
Energy E 1 E 2 E 3 Kinetic 0 ½mv 22 0 PE-g 0 0 mgh PEspring ½kx 2 0 0 Totals ½kx 2 ½mv 22 mgh 21

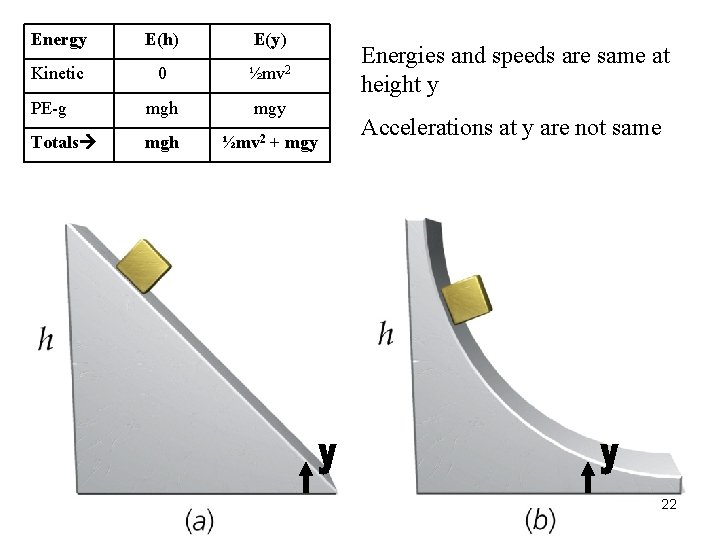
Energy Kinetic PE-g Totals E(h) E(y) 0 ½mv 2 mgh mgy mgh ½mv 2 + mgy Energies and speeds are same at height y Accelerations at y are not same 22

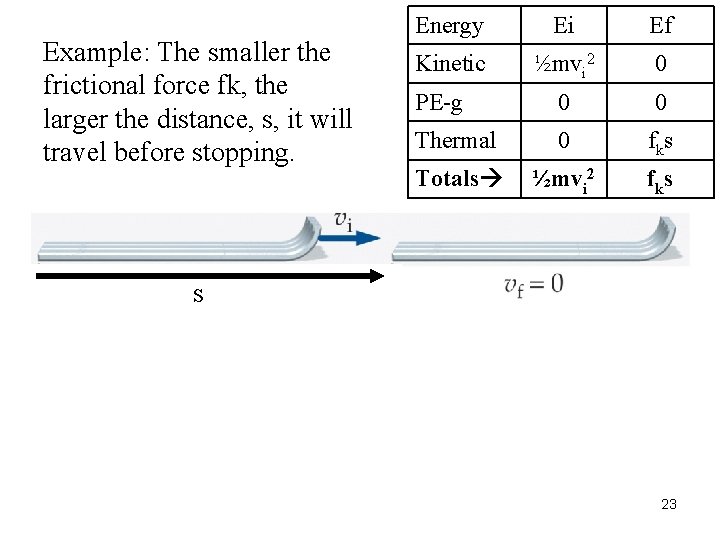
Example: The smaller the frictional force fk, the larger the distance, s, it will travel before stopping. Energy Ei Ef Kinetic ½mvi 2 0 PE-g 0 0 Thermal 0 fks Totals ½mvi 2 fk s s 23

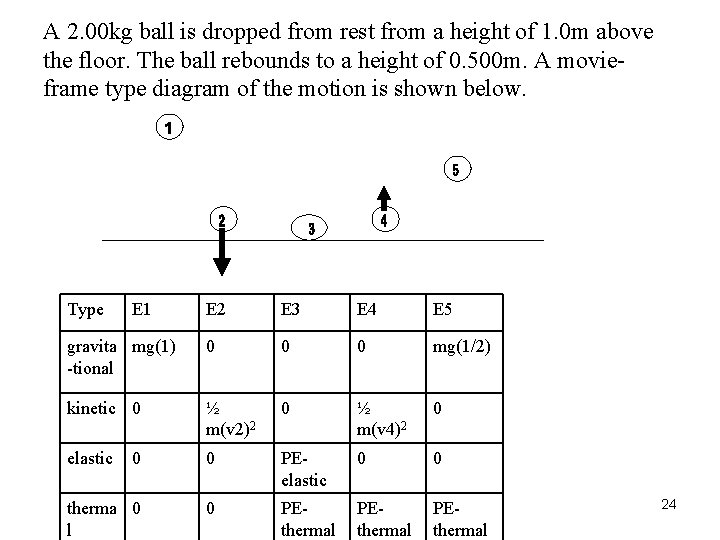
A 2. 00 kg ball is dropped from rest from a height of 1. 0 m above the floor. The ball rebounds to a height of 0. 500 m. A movieframe type diagram of the motion is shown below. Type E 1 E 2 E 3 E 4 E 5 gravita mg(1) -tional 0 0 0 mg(1/2) kinetic 0 ½ m(v 2)2 0 ½ m(v 4)2 0 elastic 0 0 PEelastic 0 0 therma 0 l 0 PEthermal 24

By energy conservation, the sum of all energies in each column is the same, = E 1 = mg(1) = 19. 6 J Calculate v 2: (use 1 st and 2 nd columns) mg(1) = ½ m(v 2)2. g = ½ (v 2)2. v 2 = 4. 43 m/s Calculate PE-thermal: (use 1 st and 5 th columns) mg(1) = mg(1/2) + PE-thermal mg(1/2) = PE-thermal = 9. 8 J 25

Calculate PE-elastic: (use 1 st and 3 rd columns) PE-elastic + PE-thermal = mg(1) PE-elastic + 9. 8 = 19. 6 PE-elastic = 9. 8 J Calculate v 4: (use 1 st and 4 th columns) ½ m(v 4)2 + PE-thermal = mg(1) ½ m(v 4)2 + 9. 8 = 19. 6 ½ m(v 4)2 = 9. 8 (v 4)2 = 2(9. 8)/2 v 4 = 3. 13 m/s 26

Terminology • E: total energy of a system • E-mech = total energy minus thermal energy • E-mech = E – Uth. 27

Power: The time rate of doing work. SI Unit: watt, W = J/s] Example: How much average power is needed to accelerate a 2000 kg car from rest to 20 m/s in 5. 0 s? work = DKE 28

Another equation for Power: Ex: A car drives at 20 m/s and experiences airdrag of 400 N. The engine must use (400 N)(20 m/s) = 8, 000 watts of engine power to overcome this force. 8, 000 watts = 10. 7 hp. What air drag force acts at 40 m/s? How much hp is needed to overcome this drag? 29

Summary • Energy measured in joules, related to motion (kinetic) or configuration (potential) • work is an energy transfer mechanism (thus can be + or -) • power is the rate of energy transfer in joules/s = watts 30

Horsepower: 1 hp = 746 watts For the previous example: 31

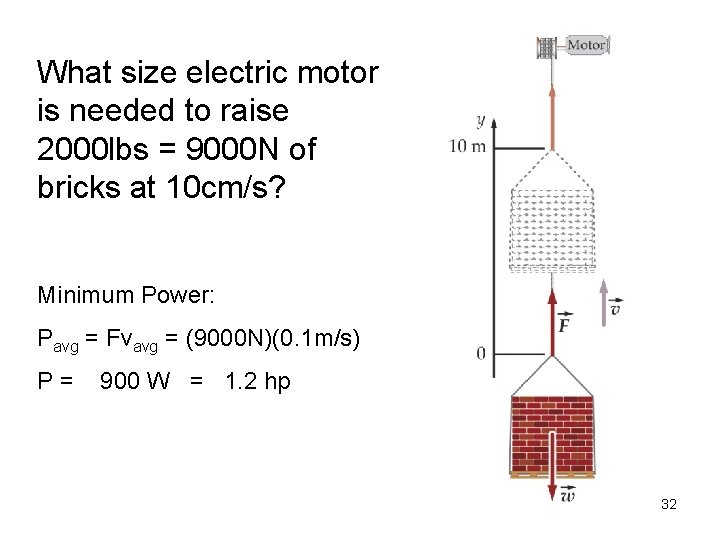
What size electric motor is needed to raise 2000 lbs = 9000 N of bricks at 10 cm/s? Minimum Power: Pavg = Fvavg = (9000 N)(0. 1 m/s) P= 900 W = 1. 2 hp 32

33

34

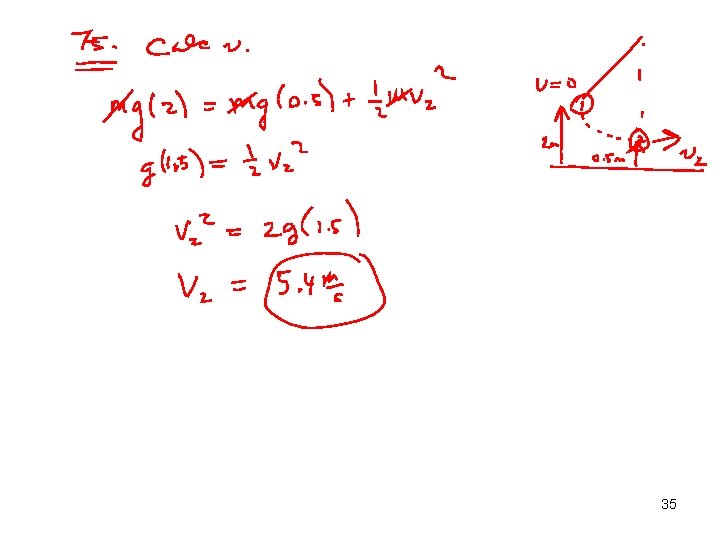
35

36

37

38

39