5 Numerical Differentiation 1 Introduction Numerical differentiation deals

5. Numerical Differentiation 1. Introduction: Numerical differentiation deals with the following problem: given the function �� = �� (�� ) find one of its derivatives at the point �� = ��. Here, the term given implies that we either have an algorithm for computing the function, or possesses a set of discrete data �� points (xi, yi), i = 1, 2, …. , n. In other words, we have a finite number of (x, y) data points or pairs from which we can compute the derivative. Numerical differentiation is a method to compute the derivatives of a function at some values of independent variable x, when the function f (x) is explicitly unknown, however it is known only for a set of arguments. Like the numerical interpolation discussed in Chapter 4, a number of formulae for differentiation are derived in this chapter. They are: (a) Derivatives based on Newton’s forward interpolation formula. This formula is used to find the derivative for some given x lying near the beginning of the data table. (b) Derivatives based on Newton’s backward interpolation formula. This formula is suitable to find the derivative for a point near the end of the data table. (c) Derivatives based on Stirling’s interpolation formula. This formula is used to find the derivative for some point lying near the middle of the tabulated value. A method to find the maxima and minima of a given function is also discussed in this chapter. Page 1 of 11

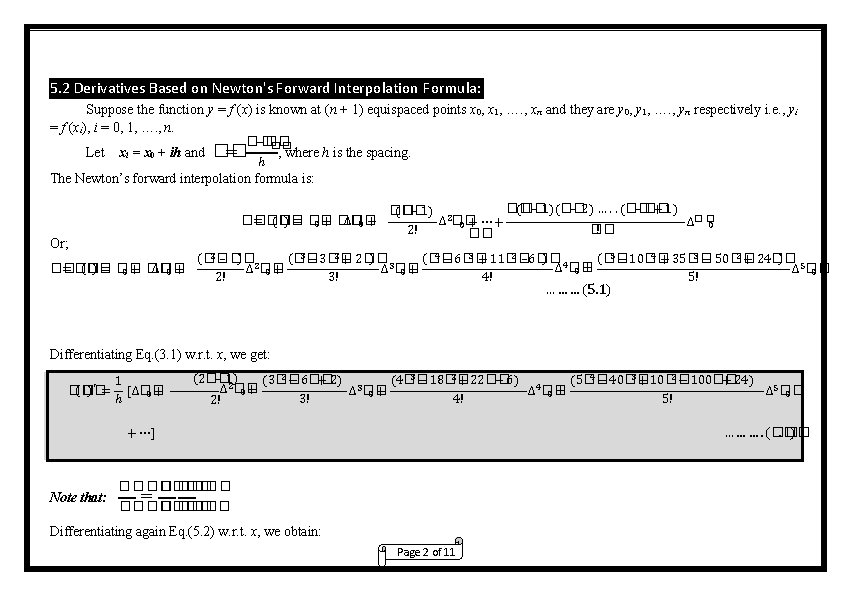
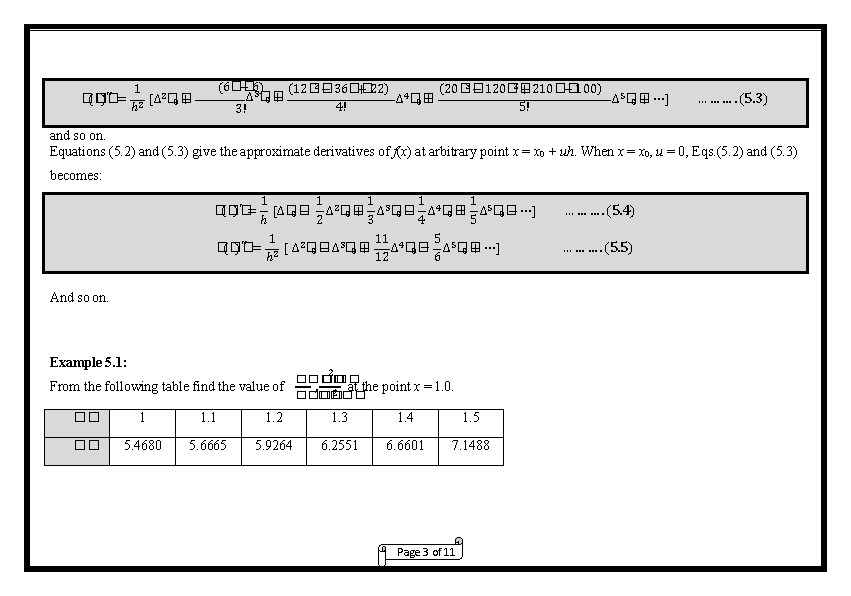
( �� ) ′′ = �� 2 − 36�� 3 − 120�� 2 + 210�� (6�� − 63) (12�� (20�� + 22) 4 − 100) 5 ∆ �� + 0+ ∆ �� 0 0 + ⋯] 4! 5! 3! 1 [∆2�� 0+ ℎ2 … … …. (5. 3) and so on. Equations (5. 2) and (5. 3) give the approximate derivatives of f(x) at arbitrary point x = x 0 + uh. When x = x 0, u = 0, Eqs. (5. 2) and (5. 3) becomes: 1 1 2 1 3 1 4 1 5 [∆�� ∆ �� 0 − 0 + ∆ �� 0 − ∆ �� 0 + ∆ �� 0 − ⋯] ℎ 2 3 4 5 1 11 4 5 5 3 ( �� ) ′′ = 2 [ ∆2�� �� ∆ �� 0 − ∆ �� 0 + ⋯] ℎ 12 6 ( �� )′ = �� And so on. Example 5. 1: 2 From the following table find the value of ���� �� �� , at the point 2 ���� x = 1. 0. �� 1 1. 2 1. 3 1. 4 1. 5 �� 5. 4680 5. 6665 5. 9264 6. 2551 6. 6601 7. 1488 Page 3 of 11 … … …. (5. 4) … … …. (5. 5)

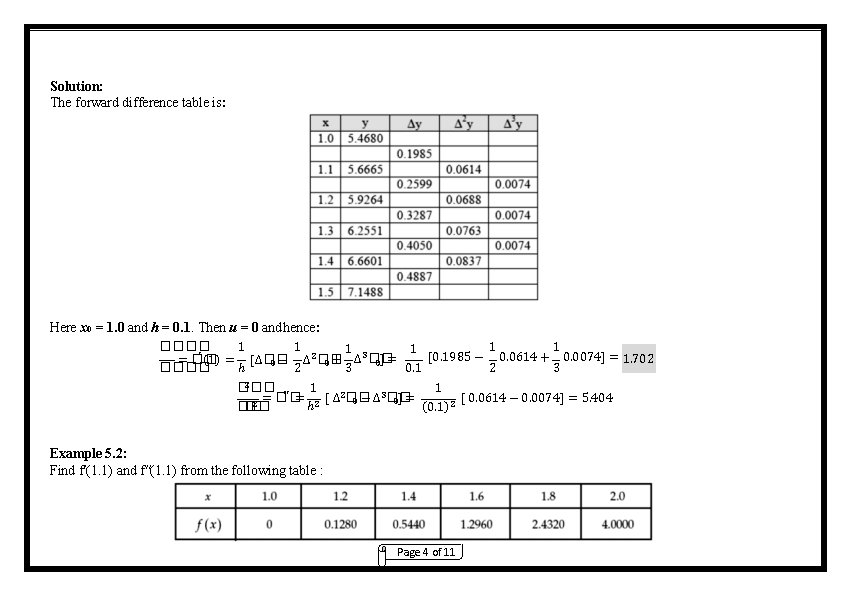
Solution: The forward difference table is: Here x 0 = 1. 0 and h = 0. 1. Then u = 0 and hence: ���� 1 1 1 3 1 ′ (1) = 2 �� [0. 1985 − 0. 0614 + 0. 0074] = 1. 702 + ∆ �� ] = = �� [∆�� − ∆ 0 0 0 ���� 2 3 ℎ 0. 1 2 3 2 �� 1 1 �� ′′ = 2�� 3�� [ ] [ 0. 0614 − 0. 0074 ] = 5. 404 = �� ∆ − ∆ = 0 0 2 ℎ2 (0. 1)2 �� �� Example 5. 2: Find f′(1. 1) and f″(1. 1) from the following table : Page 4 of 11

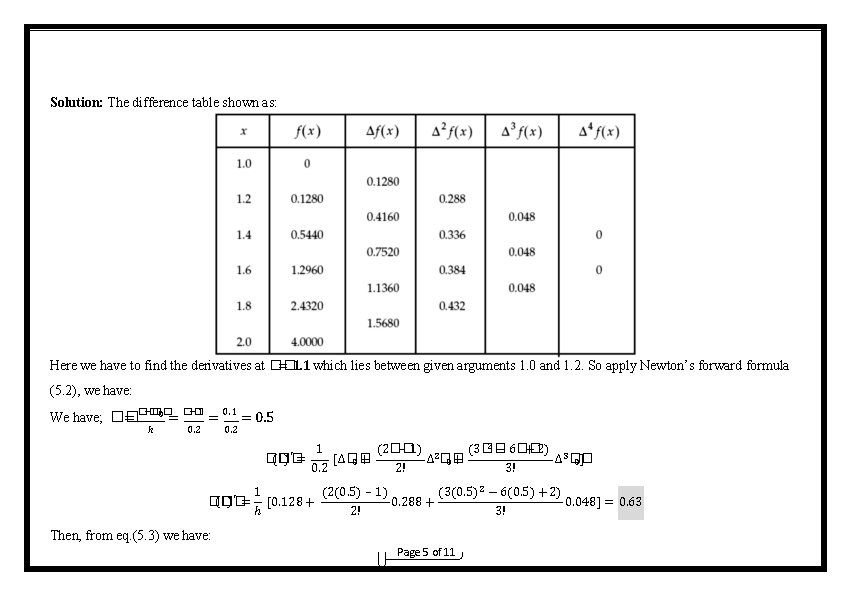
Solution: The difference table shown as: Here we have to find the derivatives at �� = 1. 1 which lies between given arguments 1. 0 and 1. 2. So apply Newton’s forward formula (5. 2), we have: �� −�� �� − 1 0 We have; �� = ℎ = 0. 2 = 0. 1 = 0. 5 0. 2 ( �� )′ = �� 2 − 6�� (2�� (3�� – 1) 2 + 2) 3 1 [∆�� + ∆ �� 0 0 0] 2! 3! 0. 2 (2(0. 5) – 1) (3(0. 5)2 − 6(0. 5) + 2) 1 [0. 128 + 0. 288 + 0. 048] = 0. 63 ℎ 2! 3! Then, from eq. (5. 3) we have: Page 5 of 11

( �� ) ′′ = �� 1 ℎ2 [∆2�� 0+ (1. 1)′′ = ∴ �� 1 (0. 5)2 (6�� − 6) 3 ∆ �� 0] 3! [0. 288 + (6(0. 5)− 6) 3! 0. 048] = 6. 6 5. 3 Derivatives Based on Newton's Backward Interpolation Formula: Suppose the function y = f (x) is known at (n + 1) equispaced points x 0, x 1, …. , xn and they are y 0, y 1, …. , yn respectively i. e. , yi = f (xi), i = 0, 1, …. , n. Let xi = x 0 + ih and �−�� �� = ℎ , where h is the spacing. The Newton’s backward interpolation formula is: (�� ) = �� (�� ) + �� �� ∇�� + �� �� (�� �� + 1) 2 ∇ �� �+ �⋯ 2! + (�� �� + 1)(�� + �� − 1) n … … (5. 6) ∇ �� �� �� ! When the Eq. (5. 6) is differentiated w. r. t. x successively, we obtain: ( �� )′ = �� 1 [∇�� + �� ℎ + ⋯] )= �� ′′(�� 2 + 6�� 3 + 18�� 2 + 22�� 4 + 40�� 3 + 10�� 2 + 100�� (2�� + 12) (3�� (4�� (5�� + 2) 3 + 6) 4 + 24) ∇ �� + �� ∇ �� + ∇5 �� �� 3! 4! 5! 2! … … …. (5. 7) 2 + 36�� 3 + 210�� (6�� (12�� (20�� 1 + 6) 3 + 22) 4 + 100) 5 2�� ∇ �� + [∇ + ∇ �� 0 0 + ⋯] 2 ℎ 3! 4! 5! … … …. (5. 8 And so on. Equations (5. 7) and (5. 8) can be used to determine the approximate differentiation of first, second, etc. order at any point x, where x = xn + uh. Page 6 of 11 )

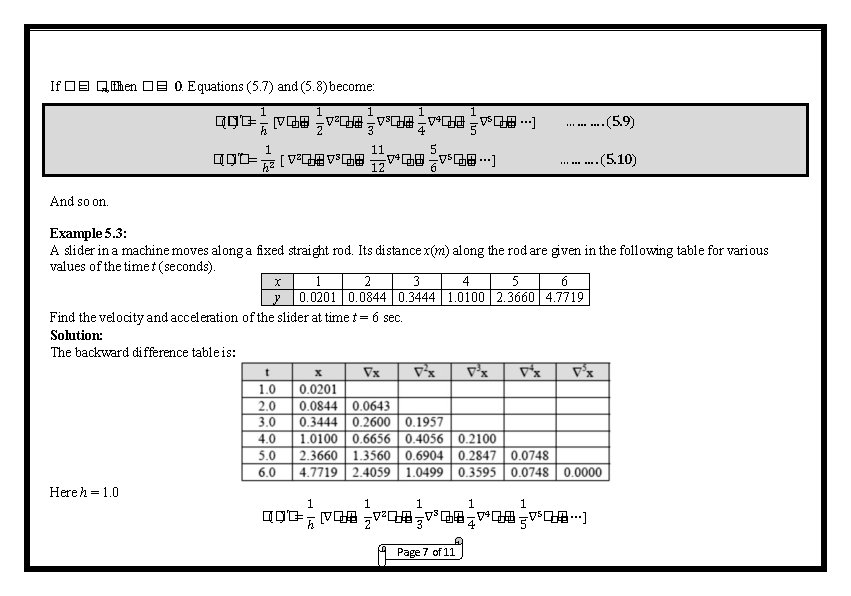
If �� = 0. Equations (5. 7) and (5. 8) become: n, then �� 1 1 1 [∇�� + ∇2�� + ∇3�� + ∇4�� + ∇5�� + ⋯] �� �� �� ℎ 2 3 4 5 1 11 4 5 ( �� ) ′′ = 2 [ ∇2�� �� + ∇3�� + ∇5�� + ⋯] �� �� ℎ 12 6 ( �� )′ = �� … … …. (5. 9) … … …. (5. 10) And so on. Example 5. 3: A slider in a machine moves along a fixed straight rod. Its distance x(m) along the rod are given in the following table for various values of the time t (seconds). x 1 2 3 4 5 6 y 0. 0201 0. 0844 0. 3444 1. 0100 2. 3660 4. 7719 Find the velocity and acceleration of the slider at time t = 6 sec. Solution: The backward difference table is: Here h = 1. 0 ( �� )′ = �� 1 ℎ 1 [∇�� �+ � 2 ∇2�� �+ � 1 3 3 ∇ �� �+ � Page 7 of 11 1 4 ∇4�� �+ � 1 5 ∇5�� �+ �⋯]

���� 1 1 [2. 4059 + 1. 0499 + 0. 3595 + 0. 0748] = 3. 0694 = ���� 1. 0 2 3 4 2 �� 11 4 1 11 2 �� 3 �� = [ ∇ + ∇ �� ] = [ 1. 0499 + 0. 3595 + 0. 0748] = 1. 478 �� �� �� 2 ℎ2 (1. 0)2 �� �� 12 12 Example 5. 4: From the following table, find the values of 2 ���� �� �� and at �� �� �� 2 �� x = 2. 03. Solution: Page 8 of 11