5 Network Design BIA 674 Supply Chain Analytics

5. Network Design BIA 674 – Supply Chain Analytics

Designing Distribution and Supply Chain Networks 1. Key design factors 2. Distribution options 3. Design of optimal distribution networks under various configurations and constraints

The Role of Distribution in the Supply Chain Distribution – the steps taken to move and store a product from the supplier stage to the customer stage in a supply chain Drives profitability by directly affecting supply chain cost and the customer experience Choice of distribution network can achieve supply chain objectives from low cost to high responsiveness 2 phases: a) structure, b) detailed specifications a) directly or through intermediaries?

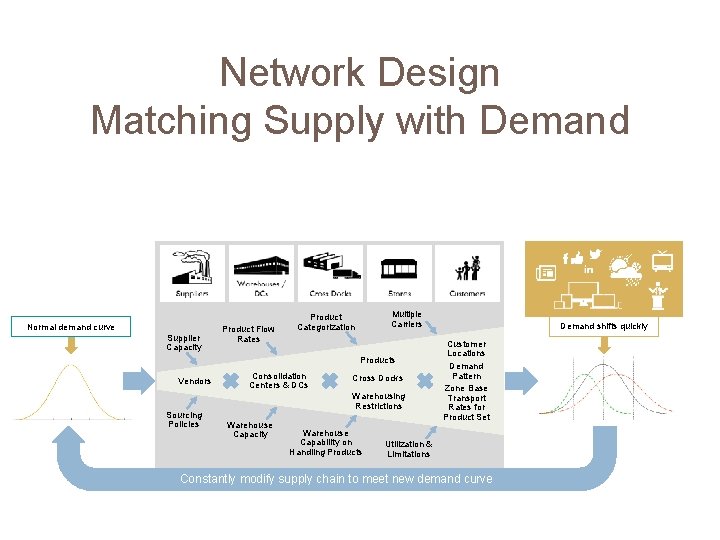
Network Design Matching Supply with Demand Normal demand curve Supplier Capacity Product Flow Rates Multiple Carriers Product Categorization Products Vendors Sourcing Policies Consolidation Centers & DCs Cross Docks Warehousing Restrictions Warehouse Capacity Warehouse Capability on Handling Products Demand shifts quickly Customer Locations Demand Pattern Zone Base Transport Rates for Product Set Utilization & Limitations Constantly modify supply chain to meet new demand curve

Factors Influencing Distribution Network Design Performance of a distribution network should be evaluated along two dimensions: 1. 2. Customer needs that are met Cost of meeting customer needs What is the impact on customer service and cost for different distribution network options? Profitability of the delivery network determined by revenue from met customer needs and network costs

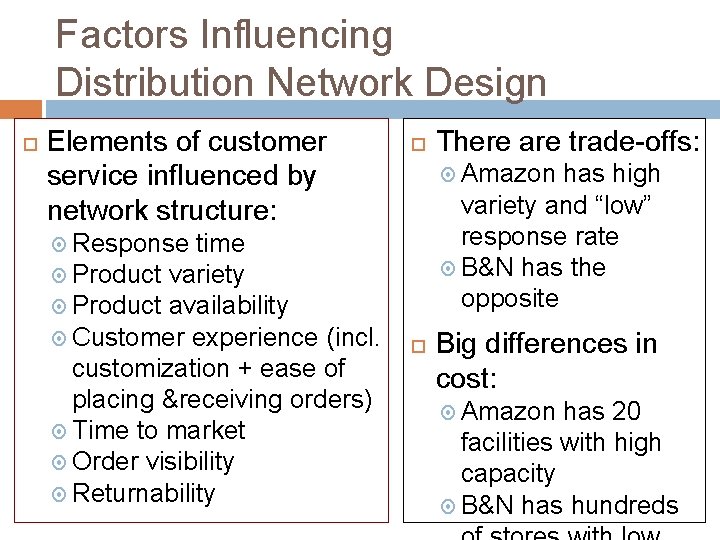
Factors Influencing Distribution Network Design Elements of customer service influenced by network structure: time Product variety Product availability Customer experience (incl. customization + ease of placing &receiving orders) Time to market Order visibility Returnability There are trade-offs: Amazon has high variety and “low” response rate B&N has the opposite Response Big differences in cost: Amazon has 20 facilities with high capacity B&N has hundreds

Factors Influencing Distribution Network Design Supply chain costs affected by network structure: Inventories Transportation Facilities and handling Information

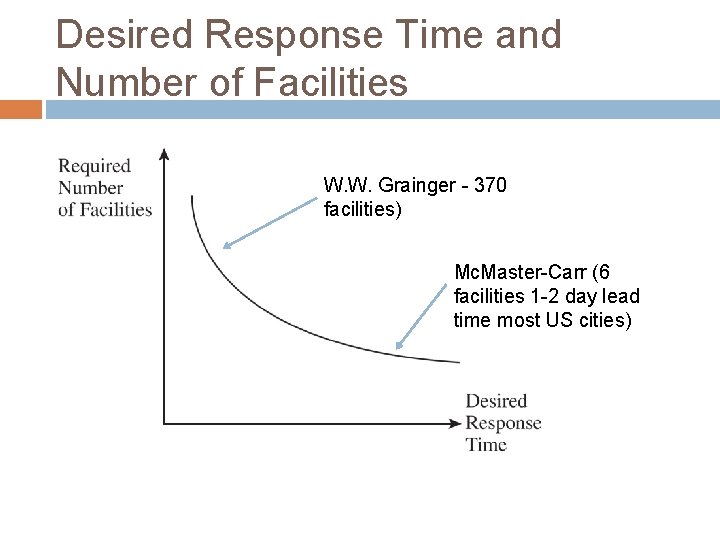
Desired Response Time and Number of Facilities W. W. Grainger - 370 facilities) Mc. Master-Carr (6 facilities 1 -2 day lead time most US cities)

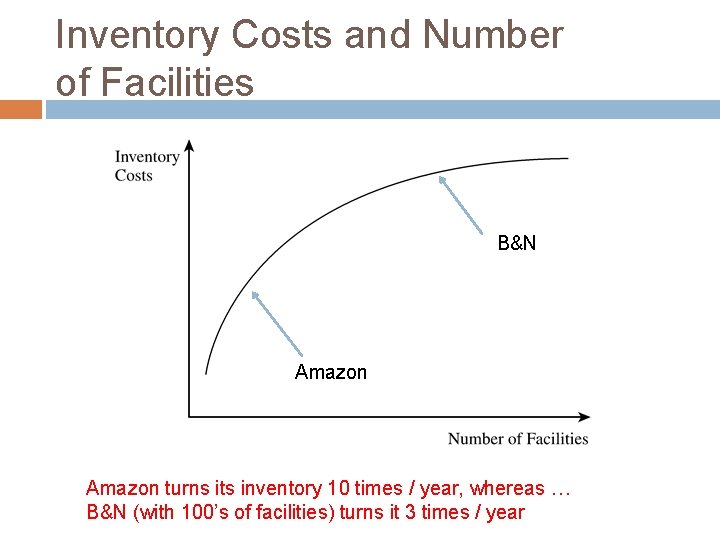
Inventory Costs and Number of Facilities B&N Amazon turns its inventory 10 times / year, whereas … B&N (with 100’s of facilities) turns it 3 times / year

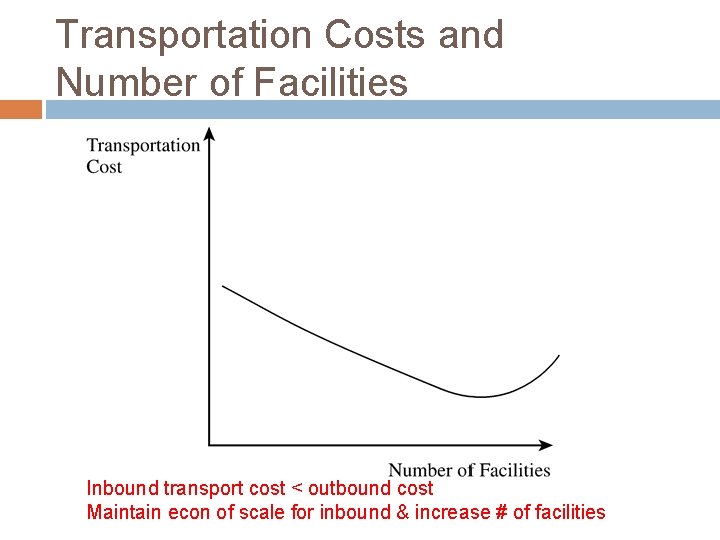
Transportation Costs and Number of Facilities Inbound transport cost < outbound cost Maintain econ of scale for inbound & increase # of facilities

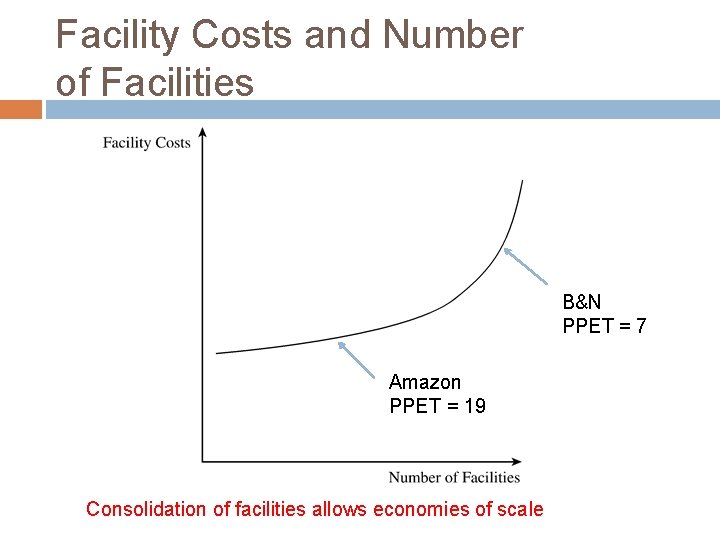
Facility Costs and Number of Facilities B&N PPET = 7 Amazon PPET = 19 Consolidation of facilities allows economies of scale

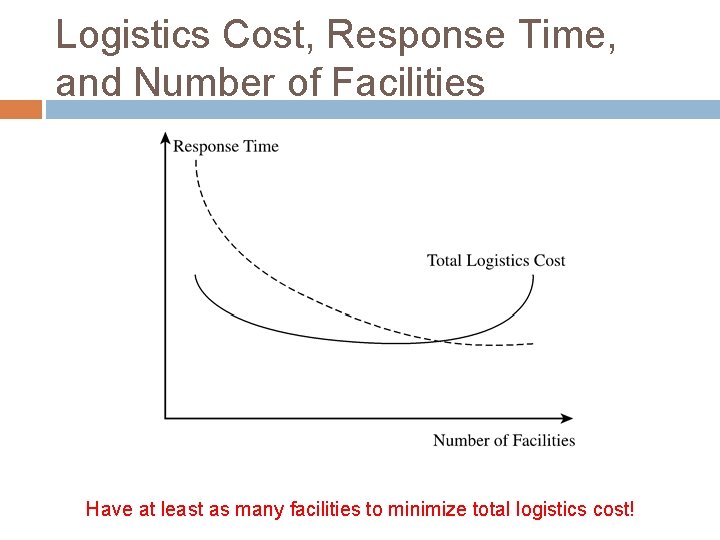
Logistics Cost, Response Time, and Number of Facilities Have at least as many facilities to minimize total logistics cost!

Design Options for a Distribution Network Distribution network choices from the manufacturer to the end consumer Two key decisions 1. 2. Will product be delivered to the customer location or picked up from a prearranged site? Will product flow through an intermediary (or intermediate location)?

Design Options for a Distribution Network One of six designs may be used 1. 2. 3. 4. 5. 6. Manufacturer storage with direct shipping (dropshipping) Manufacturer storage with direct shipping and in-transit merge Distributor storage with carrier delivery Distributor storage with last-mile delivery Manufacturer/distributor storage with customer pickup Retail storage with customer pickup

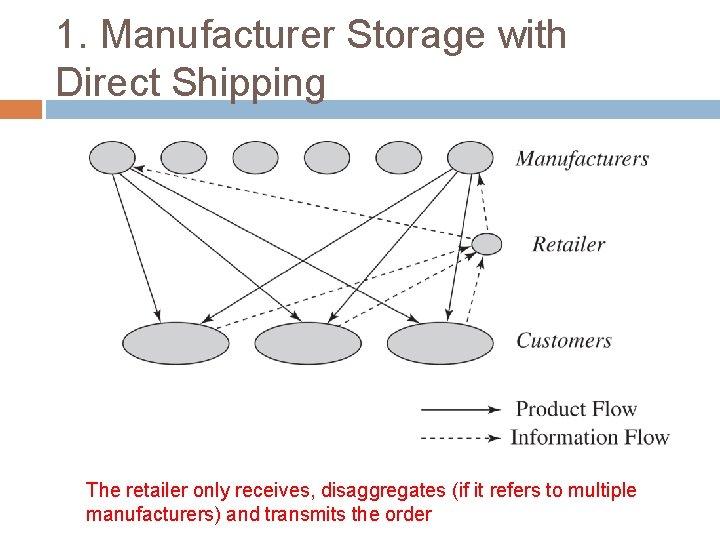
1. Manufacturer Storage with Direct Shipping The retailer only receives, disaggregates (if it refers to multiple manufacturers) and transmits the order

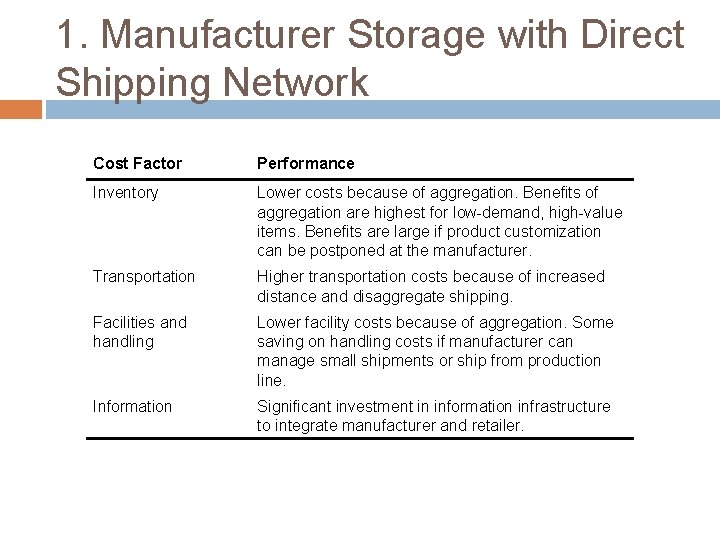
1. Manufacturer Storage with Direct Shipping Network Cost Factor Performance Inventory Lower costs because of aggregation. Benefits of aggregation are highest for low-demand, high-value items. Benefits are large if product customization can be postponed at the manufacturer. Transportation Higher transportation costs because of increased distance and disaggregate shipping. Facilities and handling Lower facility costs because of aggregation. Some saving on handling costs if manufacturer can manage small shipments or ship from production line. Information Significant investment in information infrastructure to integrate manufacturer and retailer.

1. Manufacturer Storage with Direct Shipping Network Service Factor Performance Response time Long response time of one to two weeks because of increased distance and two stages for order processing. Response time may vary by product, thus complicating receiving. Product variety Easy to provide a high level of variety. Product availability Easy to provide a high level of product availability because of aggregation at manufacturer. Customer experience Good in terms of home delivery but can suffer if order from several manufacturers is sent as partial shipments. Time to market Fast, with the product available as soon as the first unit is produced. Order visibility More difficult but also more important from a customer service perspective. Returnability Expensive and difficult to implement.

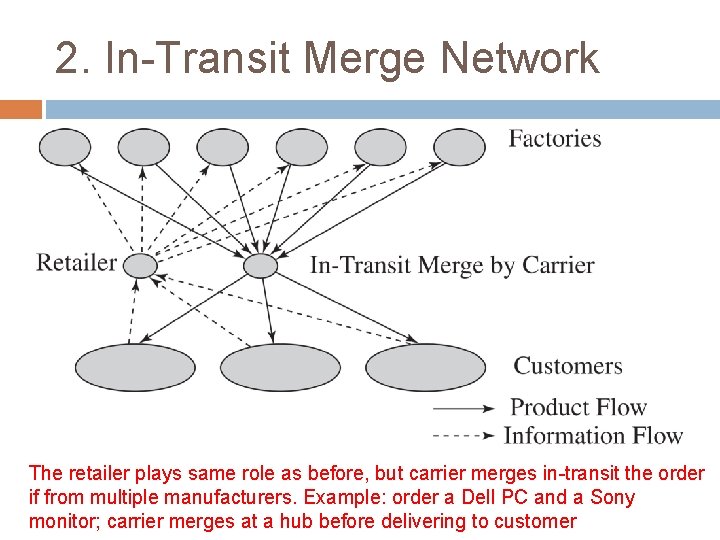
2. In-Transit Merge Network The retailer plays same role as before, but carrier merges in-transit the order if from multiple manufacturers. Example: order a Dell PC and a Sony monitor; carrier merges at a hub before delivering to customer

2. In-Transit Merge Cost Factor Performance Inventory Similar to drop-shipping. Transportation Somewhat lower transportation costs than drop-shipping. Facilities and handling Handling costs higher than drop-shipping at carrier; receiving costs lower at customer. Information Investment is somewhat higher than for dropshipping.

2. In-Transit Merge Service Factor Performance Response time Similar to drop-shipping; may be marginally higher. Product variety Similar to drop-shipping. Product availability Similar to drop-shipping. Customer experience Better than drop-shipping because only a single delivery has to be received. Time to market Similar to drop-shipping. Order visibility Similar to drop-shipping. Returnability Similar to drop-shipping.

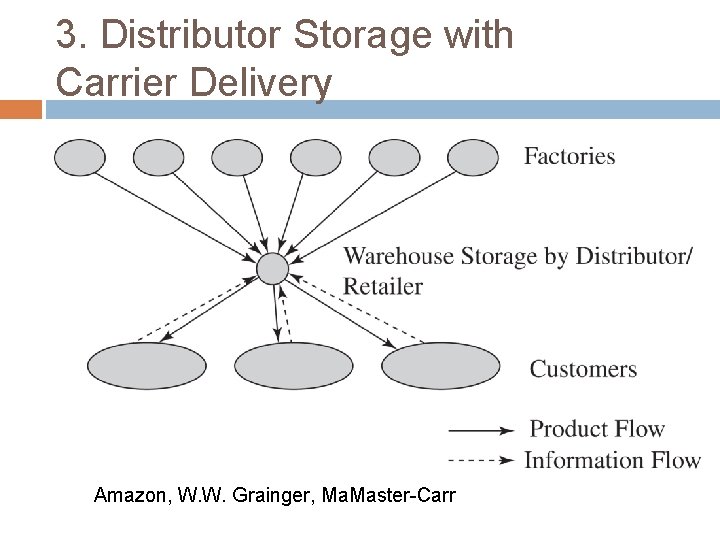
3. Distributor Storage with Carrier Delivery Amazon, W. W. Grainger, Ma. Master-Carr

3. Distributor Storage with Carrier Delivery Cost Factor Performance Inventory Higher than manufacturer storage. Difference is not large for faster moving items but can be large for very slowmoving items. Transportation Lower than manufacturer storage. Reduction is highest for faster moving items. Facilities and handling Somewhat higher than manufacturer storage. The difference can be large for very slow-moving items. Information Simpler infrastructure compared to manufacturer storage.

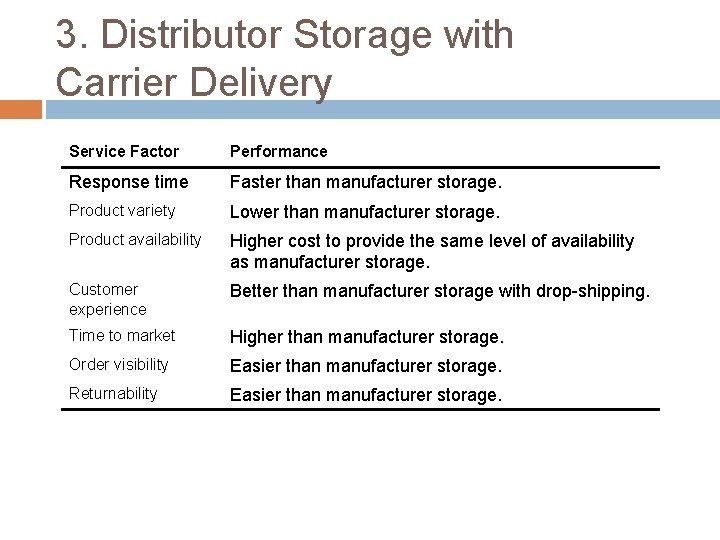
3. Distributor Storage with Carrier Delivery Service Factor Performance Response time Faster than manufacturer storage. Product variety Lower than manufacturer storage. Product availability Higher cost to provide the same level of availability as manufacturer storage. Customer experience Better than manufacturer storage with drop-shipping. Time to market Higher than manufacturer storage. Order visibility Easier than manufacturer storage. Returnability Easier than manufacturer storage.

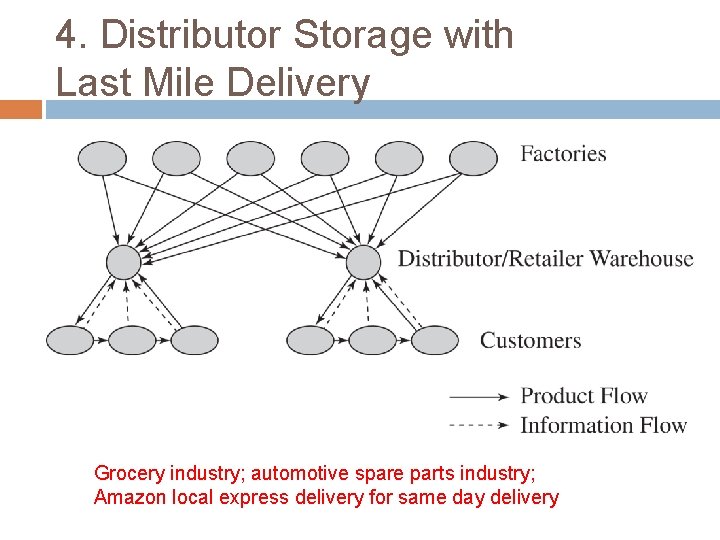
4. Distributor Storage with Last Mile Delivery Grocery industry; automotive spare parts industry; Amazon local express delivery for same day delivery

4. Distributor Storage with Last Mile Delivery Cost Factor Performance Inventory Higher than distributor storage with package carrier delivery, because of lower aggregation Transportation Very high cost given minimal scale economies. Higher than any other distribution option. Facilities and handling Facility costs higher than manufacturer storage or distributor storage with package carrier delivery, but lower than a chain of retail stores. Information Similar to distributor storage with package carrier delivery.

4. Distributor Storage with Last Mile Delivery Service Factor Performance Response time Very quick. Same day to next-day delivery. Product variety Somewhat less than distributor storage with package carrier delivery but larger than retail stores. Product availability More expensive to provide availability than any other option except retail stores. Customer experience Very good, particularly for bulky items. Slightly higher than distributor storage with package carrier delivery. Time to market Less of an issue and easier to implement than manufacturer storage or distributor storage with package carrier delivery. Order visibility Easier to implement than other previous options. Returnability Harder and more expensive than a retail network.

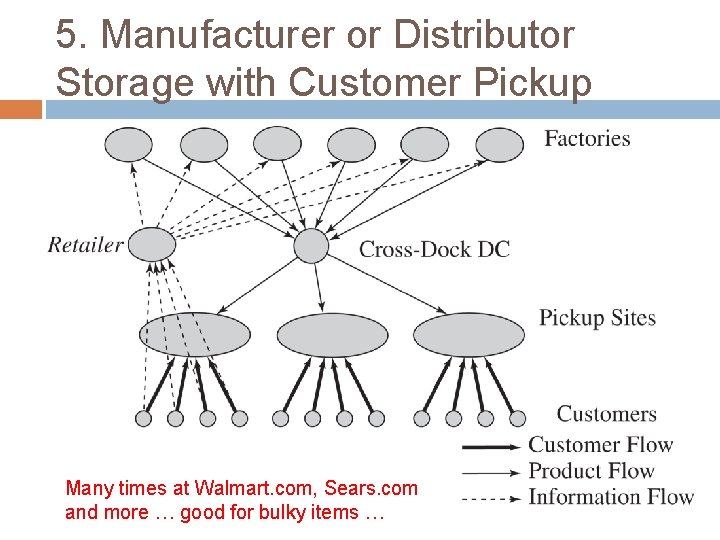
5. Manufacturer or Distributor Storage with Customer Pickup Many times at Walmart. com, Sears. com and more … good for bulky items …

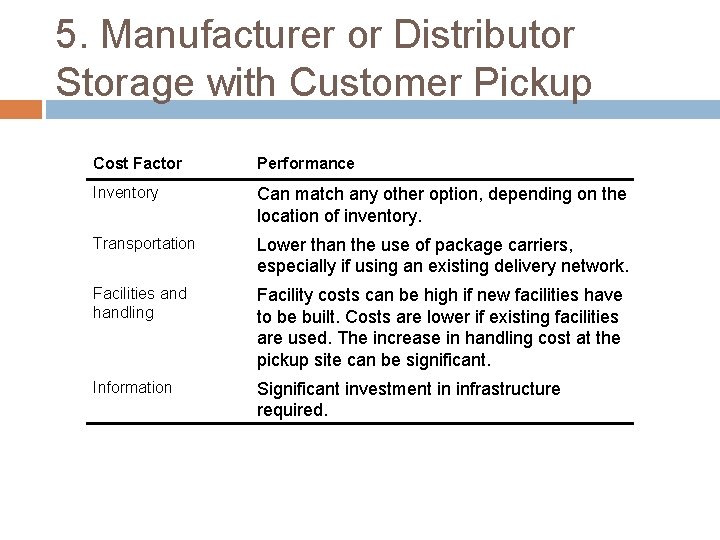
5. Manufacturer or Distributor Storage with Customer Pickup Cost Factor Performance Inventory Can match any other option, depending on the location of inventory. Transportation Lower than the use of package carriers, especially if using an existing delivery network. Facilities and handling Facility costs can be high if new facilities have to be built. Costs are lower if existing facilities are used. The increase in handling cost at the pickup site can be significant. Information Significant investment in infrastructure required.

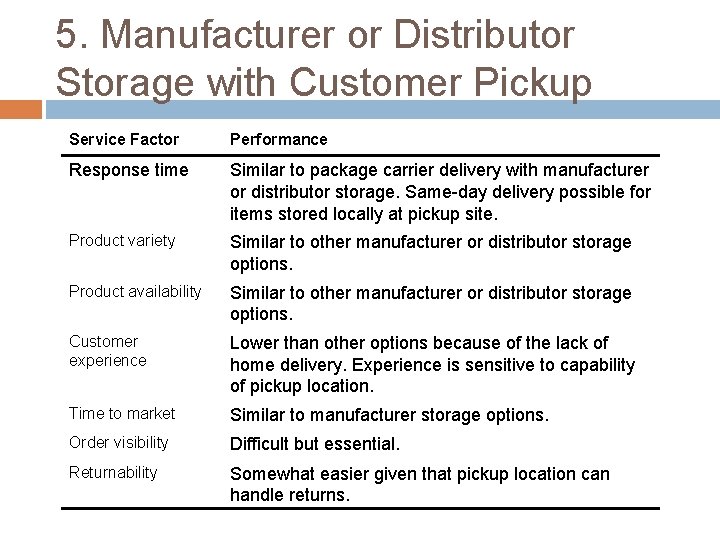
5. Manufacturer or Distributor Storage with Customer Pickup Service Factor Performance Response time Similar to package carrier delivery with manufacturer or distributor storage. Same-day delivery possible for items stored locally at pickup site. Product variety Similar to other manufacturer or distributor storage options. Product availability Similar to other manufacturer or distributor storage options. Customer experience Lower than other options because of the lack of home delivery. Experience is sensitive to capability of pickup location. Time to market Similar to manufacturer storage options. Order visibility Difficult but essential. Returnability Somewhat easier given that pickup location can handle returns.

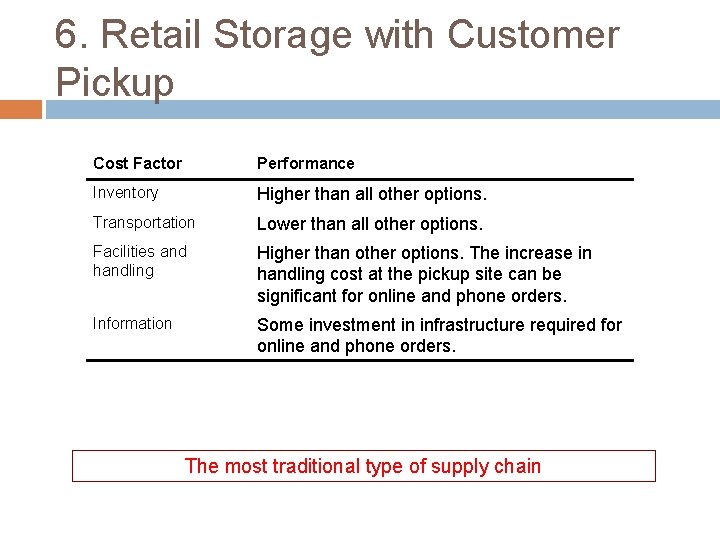
6. Retail Storage with Customer Pickup Cost Factor Performance Inventory Higher than all other options. Transportation Lower than all other options. Facilities and handling Higher than other options. The increase in handling cost at the pickup site can be significant for online and phone orders. Information Some investment in infrastructure required for online and phone orders. The most traditional type of supply chain

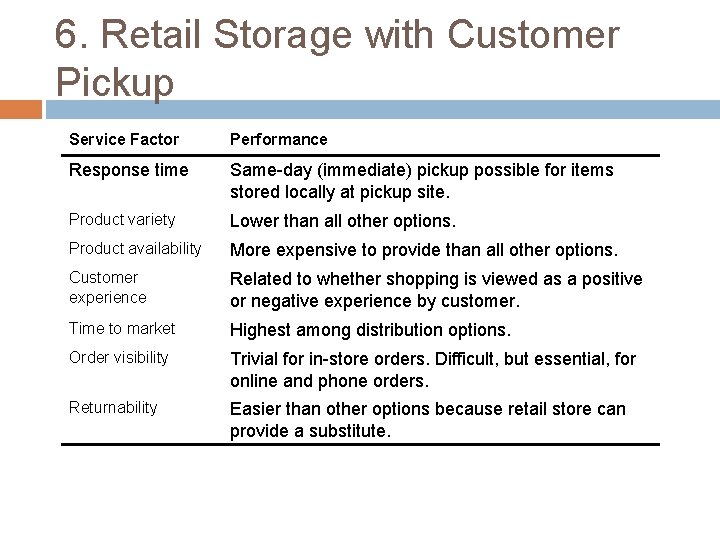
6. Retail Storage with Customer Pickup Service Factor Performance Response time Same-day (immediate) pickup possible for items stored locally at pickup site. Product variety Lower than all other options. Product availability More expensive to provide than all other options. Customer experience Related to whether shopping is viewed as a positive or negative experience by customer. Time to market Highest among distribution options. Order visibility Trivial for in-store orders. Difficult, but essential, for online and phone orders. Returnability Easier than other options because retail store can provide a substitute.

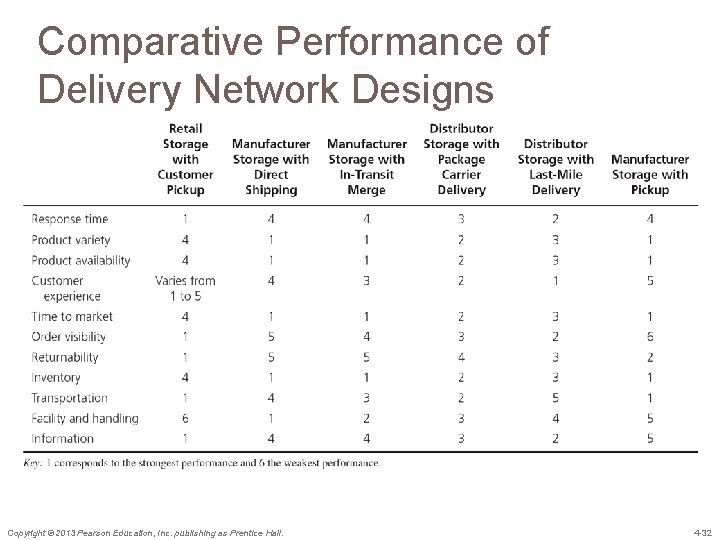
Comparative Performance of Delivery Network Designs Copyright © 2013 Pearson Education, Inc. publishing as Prentice Hall. 4 -32

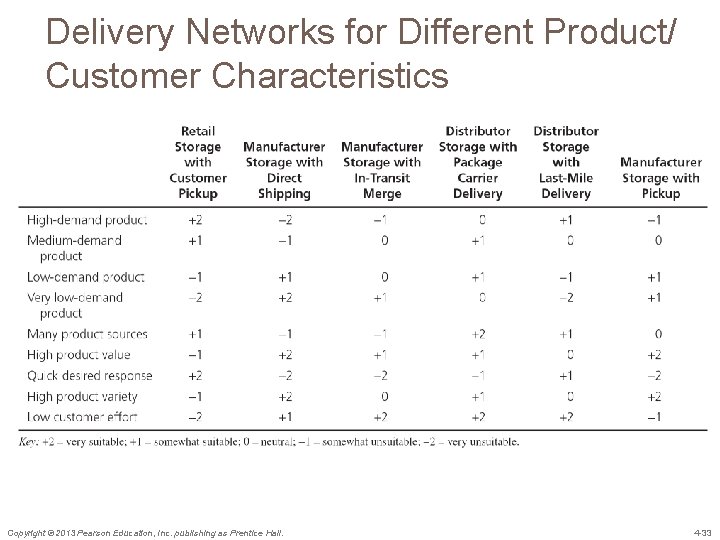
Delivery Networks for Different Product/ Customer Characteristics Copyright © 2013 Pearson Education, Inc. publishing as Prentice Hall. 4 -33

A Framework for Network Design Decisions 1. Role of network design in a supply chain. 2. Factors influencing supply chain network design decisions. 3. Framework for making network design decisions.

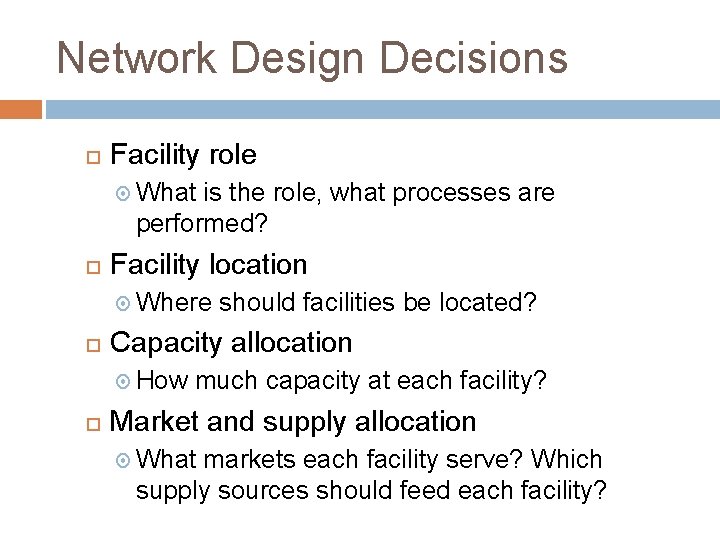
Network Design Decisions Facility role What is the role, what processes are performed? Facility location Where Capacity allocation How should facilities be located? much capacity at each facility? Market and supply allocation What markets each facility serve? Which supply sources should feed each facility?

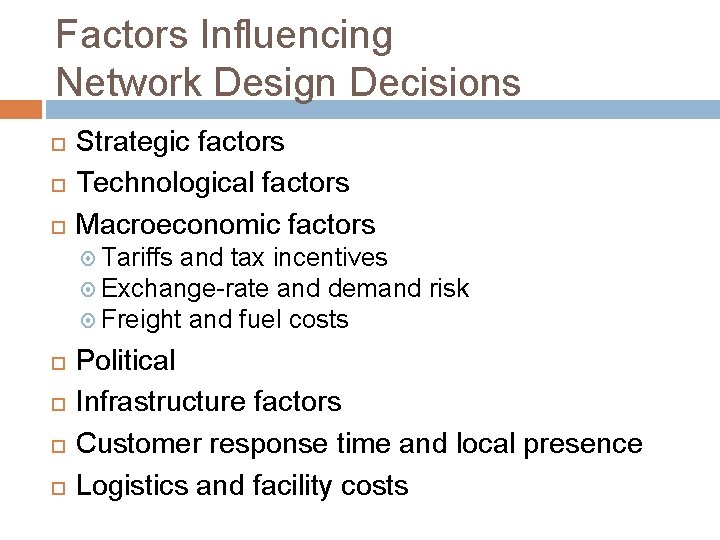
Factors Influencing Network Design Decisions Strategic factors Technological factors Macroeconomic factors Tariffs and tax incentives Exchange-rate and demand risk Freight and fuel costs Political Infrastructure factors Customer response time and local presence Logistics and facility costs

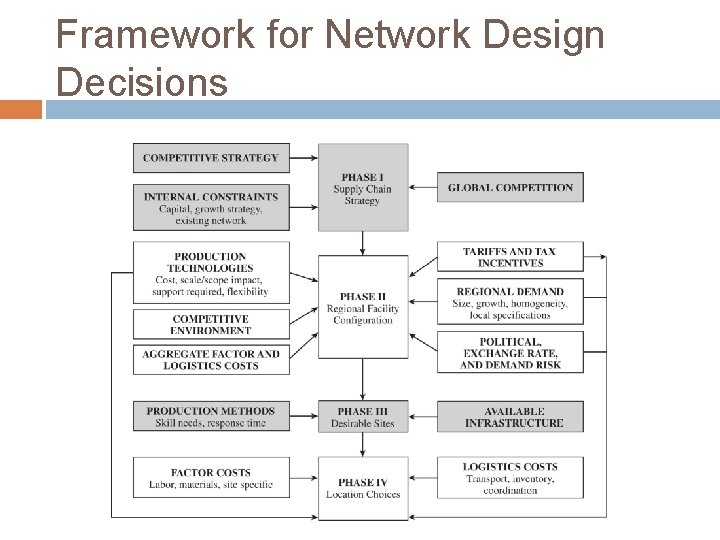
Framework for Network Design Decisions

Mathematical Models & Examples 1. Capacitated Plant Location Models 2. Practical considerations 3. Advanced models with multiple attributes

Models for Facility Location and Capacity Allocation Network design models are used to decide on locations and capacities, and to assign current demand to facilities Objective: Maximize the overall profitability of the supply chain network, while providing customers with the appropriate responsiveness Many trade-offs during network design

Network Optimization Models and Numerical Examples Capacitated Plant Location Models (also known as Facility Location and Capacity Allocation Models) Model 1: Optimal Production Allocation or Transshipment Problem Model 2: Consider location specific costs and decide which plants should remain open Model 3: Enforce single sourcing for each market Model 4: Consider multiple plant capacity scenarios

Network Model 1: Transportation Problem The (simple) Transportation Problem Shipment of a single product from a set of suppliers to a set of customers (or similarly allocating demand to production facilities) Input parameters: Capacities: the maximum amount of products a supplier can ship in a given amount of time Demand: the customer demand (typically estimated from demand forecasting models) Shipping cost: the shipping cost (per unit of product) for each possible supplier-customer pair

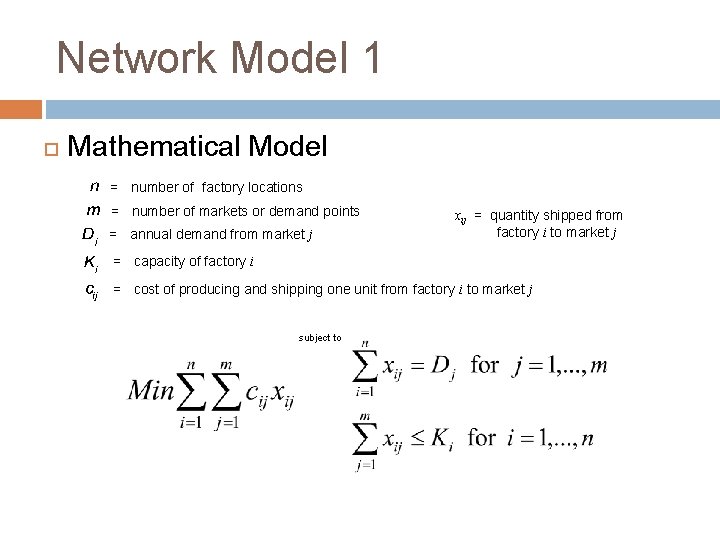
Network Model 1 Mathematical Model = number of factory locations = number of markets or demand points = annual demand from market j xij = quantity shipped from factory i to market j = capacity of factory i = cost of producing and shipping one unit from factory i to market j subject to

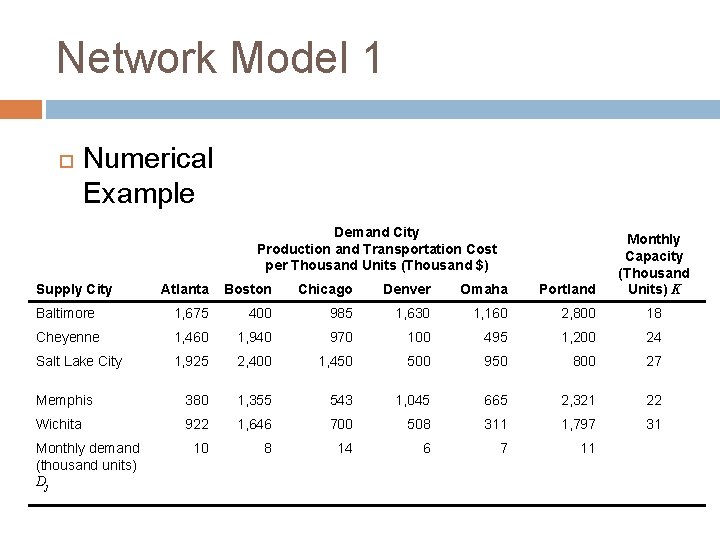
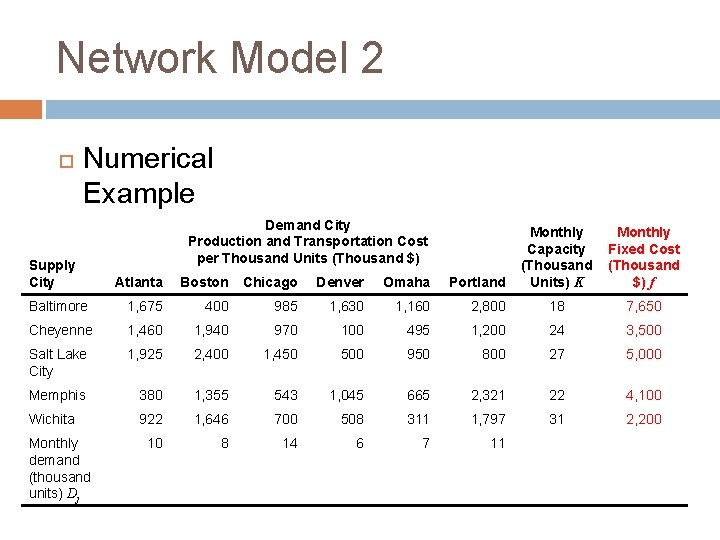
Network Model 1 Numerical Example Demand City Production and Transportation Cost per Thousand Units (Thousand $) Monthly Capacity (Thousand Units) K Atlanta Boston Chicago Denver Omaha Portland Baltimore 1, 675 400 985 1, 630 1, 160 2, 800 18 Cheyenne 1, 460 1, 940 970 100 495 1, 200 24 Salt Lake City 1, 925 2, 400 1, 450 500 950 800 27 Memphis 380 1, 355 543 1, 045 665 2, 321 22 Wichita 922 1, 646 700 508 311 1, 797 31 10 8 14 6 7 11 Supply City Monthly demand (thousand units) Dj

Network model 1 Formulation of the model Min Z = 1675 x 11 + 400 X 12 +. . . + 311 X 55 + 1797 X 56 s. t. X 11 + X 21 +. . . + X 51 = 10 …. X 16 + X 26 +. . . + X 56 = 7 X 11 + X 12 +. . . + X 16 …. X 51 + X 52 +. . . + X 56 ≤ 18 ≤ 31 Xij 0 Satisfy the demand of each demand city Do not exceed the capacity

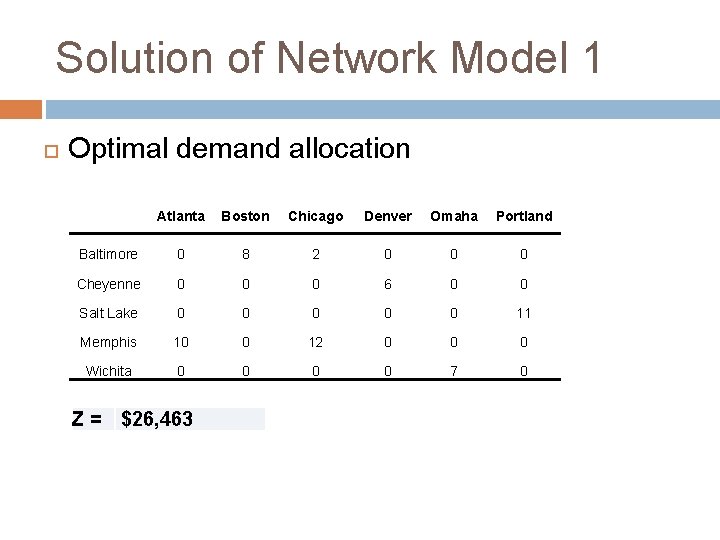
Solution of Network Model 1 Optimal demand allocation Atlanta Boston Chicago Denver Omaha Portland Baltimore 0 8 2 0 0 0 Cheyenne 0 0 0 6 0 0 Salt Lake 0 0 0 11 Memphis 10 0 12 0 0 0 Wichita 0 0 7 0 Z = $26, 463

Network Model 2: Selecting plants Given that you can meet supply with less plants, decide which plants should remain open There are now location-specific costs to consider! yi = 1 if factory i is open, 0 otherwise xij = quantity shipped from factory i to market j

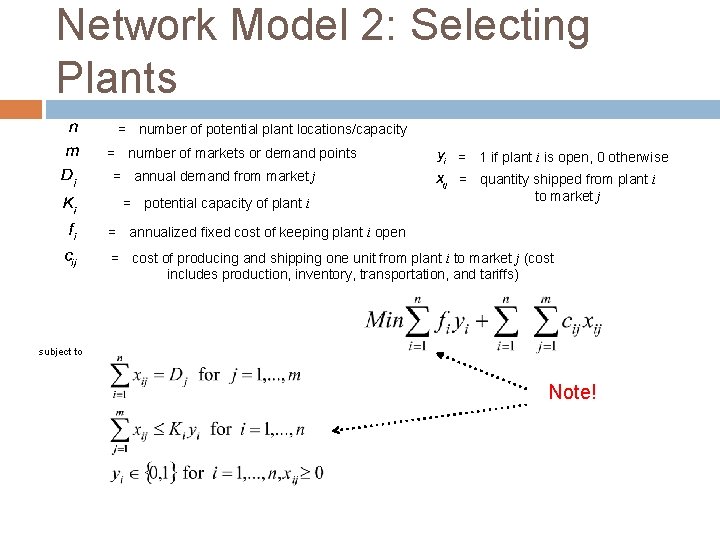
Network Model 2: Selecting Plants = number of potential plant locations/capacity = number of markets or demand points = annual demand from market j = potential capacity of plant i = 1 if plant i is open, 0 otherwise = quantity shipped from plant i to market j = annualized fixed cost of keeping plant i open = cost of producing and shipping one unit from plant i to market j (cost includes production, inventory, transportation, and tariffs) subject to Note!

Network Model 2 Numerical Example Supply City Demand City Production and Transportation Cost per Thousand Units (Thousand $) Monthly Capacity (Thousand Units) K Monthly Fixed Cost (Thousand $) f Atlanta Boston Chicago Denver Omaha Portland Baltimore 1, 675 400 985 1, 630 1, 160 2, 800 18 7, 650 Cheyenne 1, 460 1, 940 970 100 495 1, 200 24 3, 500 Salt Lake City 1, 925 2, 400 1, 450 500 950 800 27 5, 000 Memphis 380 1, 355 543 1, 045 665 2, 321 22 4, 100 Wichita 922 1, 646 700 508 311 1, 797 31 2, 200 10 8 14 6 7 11 Monthly demand (thousand units) Dj

Network Model 2 Formulation of the model Min Z = 7650 Y 1+…+ 2200 Y 5+ +1675 x 11 + 400 X 12 +. . . + 311 X 55 + 1797 X 56 s. t. X 11 + X 21 +. . . + X 51 = 10 …. X 16 + X 26 +. . . + X 56 = 7 X 11 + X 12 +. . . + X 16 …. X 51 + X 52 +. . . + X 56 ≤ 18 Y 1 ≤ 31 Y 5 Xij Yi = 0 0/1 Satisfy the demand of each demand city Do not exceed the capacity

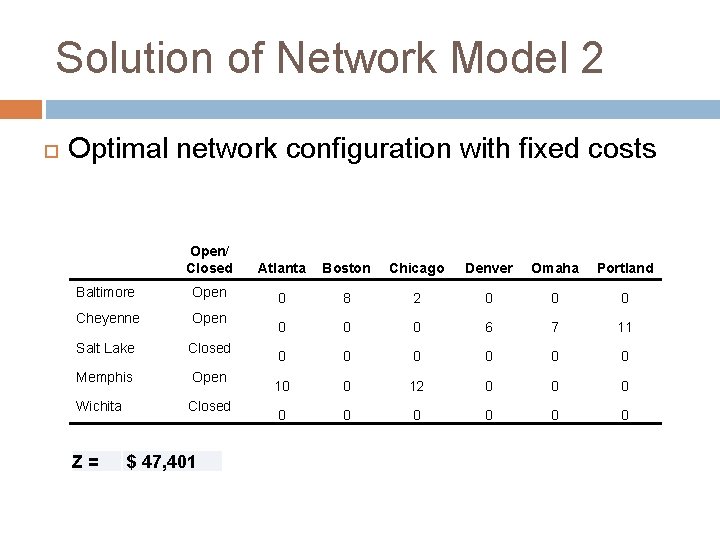
Solution of Network Model 2 Optimal network configuration with fixed costs Open/ Closed Atlanta Boston Chicago Denver Omaha Portland Baltimore Open 0 8 2 0 0 0 Cheyenne Open 0 0 0 6 7 11 Salt Lake Closed 0 0 0 Memphis Open 10 0 12 0 0 0 0 0 Wichita Z= Closed $ 47, 401

Network Model 3: Single sourcing Each market should be supplied by only one factory Modify objective, constraints & decision yi = 1 if factory i is open, 0 otherwise variables xij =as 1 iffollows: market j is supplied by factory i, 0 otherwise subject to Note!

Network Model 3 Present the formulation of the model Min Z = 7650*Y 1+…+ 2200*Y 5+ +10*1675*x 11 + 8*400*X 12 +. . . + 7*311*X 55 + 11*1797 X 56 s. t. X 11 + X 21 +. . . + X 51 = 1 One supplier …. for each demand city X 16 + X 26 +. . . + X 56 = 1 10*X 11 + 8*X 12 +. . . + 11*X 16 …. 10*X 51 + 8*X 52 +. . . + 11*X 56 Yi, Xij ≤ 18*Y 1 ≤ 31*Y 5 = 0/1 Do not exceed the capacity

Solution to Network Model 3 Optimal network configuration with single sourcing Open/ Closed Atlanta Boston Chicago Denver Omaha Portland Baltimore Closed 0 0 0 Cheyenne Closed 0 0 0 Salt Lake Open 0 0 0 6 0 11 Memphis Open 10 8 0 0 Wichita Open 0 0 14 0 7 0 Z= $49, 717

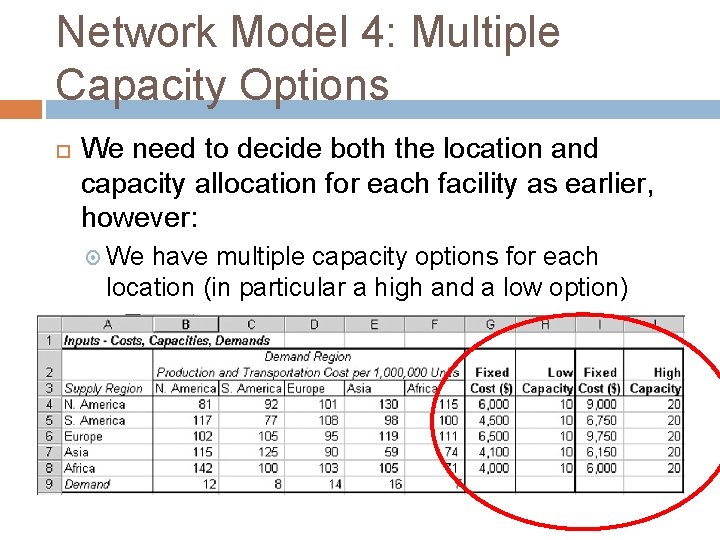
Network Model 4: Multiple Capacity Options We need to decide both the location and capacity allocation for each facility as earlier, however: We have multiple capacity options for each location (in particular a high and a low option)

Network Model 4 Modelling approach: Treat each scenario option as a separate facility and introduce binary variables for each one of them as earlier. For example: Binary variables Y 1 and Y 5 will refer to N. America, and will denote the low and high capacity, respectively. Add a constraint to make sure that only one capacity will be realized! e. g. Y 1+Y 5 ≤ 1

Network Model 4 Formulation of the model Min Z = 6000 Y 1+…+ 4000 Y 5+ + 9000 Y 6+…+6000 Y 10 +1675 x 11 + 400 X 12 +. . . + 311 X 55 + 1797 X 56 +1675 x 61 + 400 X 62 +. . . + 311 X 12, 5 + 1797 X 10, 6 s. t. (X 11 + X 21 +. . . + X 51) + (X 61 + X 71 +. . . + X 101) = 10 …. (X 16 + X 26 +. . . + X 56) + (X 66 + X 76 +. . . + X 10, 6) = 7 Satisfy the demand of each demand city (X 11 + X 12 +. . . + X 16) + (X 61 + X 62 +. . . + X 66) ≤ 18(Y 1+Y 6) …. (X 51 + X 52 +. . . + X 56) + (X 10, 1 + X 10, 2 +. . . + X 10, 6) ≤ 31(Y 5+Y 10) Y 1+Y 6 ≤ 1 …. Y 5+Y 10 ≤ 1 Xij 0 and Yi = 0/1 Do not exceed the capacity Make sure that at most only one capacity scenario will be realized for each location

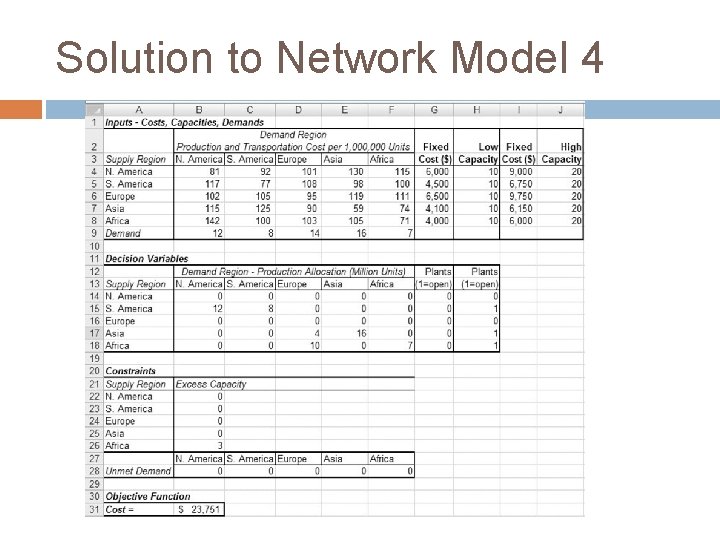
Solution to Network Model 4

Network Optimization Models and Examples cont. What happens if I have a complex network with multiple transshipment points and transportation capacities? If the supply chain network is given, and no fixed costs are associated with the use of particular facilities or locations, then the problem can be initially modeled as the socalled minimum cost network flow problem!

Minimum Cost Network Flow Basic Assumptions Ship products from a set of locations to another set of locations Assume a network with multiple nodes and links The nodes can be suppliers, demanders and transshipment points The demand of demanders and the supply capacities of suppliers are know Each link has a known capacity and unit cost Inflows and outflows can be associated with any node

Network Model 5: Network Flow for Single Product Minimum cost network flow model - Single Product All plants (or suppliers) have the same production cost A single product and a single mode of transportation Shipping cost among all connections are known Capacity of the plants (in ton per year) and demand from customers is also known Uniform flow restrictions among all arcs of the network Capacity constraints on the amount of product that can be moved between any two nodes Determine the minimum cost shipping schedule so that demand is met and plant capacities are not exceeded

Network Model 5 Mathematical Model xij = quantity shipped from node i to node j = demand or supply of a node j, and it can be positive or negative or zero = capacity of an arc ij of the network = cost of producing and shipping one unit from node i to node j subject to

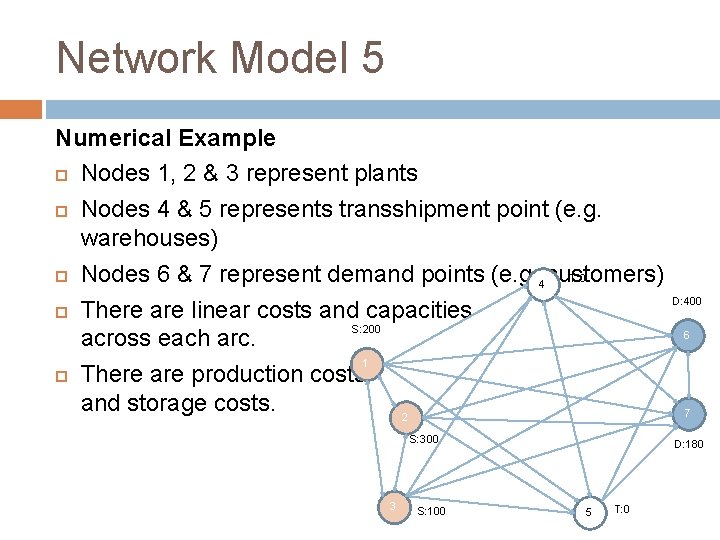
Network Model 5 Numerical Example Nodes 1, 2 & 3 represent plants Nodes 4 & 5 represents transshipment point (e. g. warehouses) Nodes 6 & 7 represent demand points (e. g. 4 customers) T: 0 There are linear costs and capacities S: 200 across each arc. 1 There are production costs and storage costs. 2 S: 300 3 S: 100 D: 400 6 7 D: 180 5 T: 0

Network Model 5 Numerical Example (cont. ) At most 200 tons of product can be moved between any two nodes

Network model 5 Formulation of the model Min Z = 5 X 12+3 X 13+5 X 14+5 X 15+20 X 16+20 X 17+. . . + 1 X 67 + 7 X 76 s. t. Node 1: (X 12 + X 13 +. . . + X 17) – (X 21 + X 31) = 200 Node 2: (X 21 + X 23 +. . . + X 27) – (X 12 + X 32) = 300 Node 3: (X 32 + X 31 +. . . + X 37) – (X 13 + X 23) = 100 Node 4: (X 14 + X 24 + X 34 + X 54) – (X 45 + X 46 + X 47) = 0 Node 5: (X 15 + X 25 + X 35 + X 45) – (X 54 + X 56 + X 57) = 0 Node 6: X 67 - (X 16 + X 26 +. . . + X 76) = - 180 Node 7: X 76 - (X 17 + X 27 +. . . + X 67) = - 400 Xij 0 and Xij ≤ 200

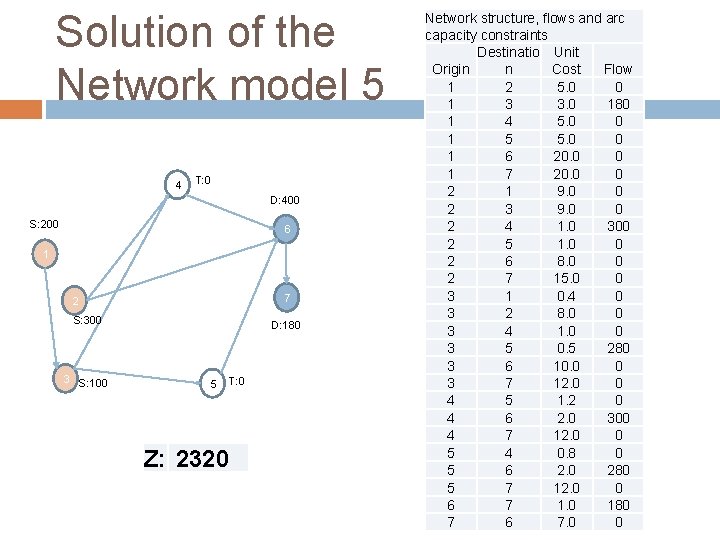
Solution of the Network model 5 4 T: 0 D: 400 S: 200 6 1 7 2 S: 300 3 S: 100 D: 180 5 T: 0 Z: 2320 Network structure, flows and arc capacity constraints Destinatio Unit Origin n Cost Flow 1 2 5. 0 0 1 3 3. 0 180 1 4 5. 0 0 1 5 5. 0 0 1 6 20. 0 0 1 7 20. 0 0 2 1 9. 0 0 2 3 9. 0 0 2 4 1. 0 300 2 5 1. 0 0 2 6 8. 0 0 2 7 15. 0 0 3 1 0. 4 0 3 2 8. 0 0 3 4 1. 0 0 3 5 0. 5 280 3 6 10. 0 0 3 7 12. 0 0 4 5 1. 2 0 4 6 2. 0 300 4 7 12. 0 0 5 4 0. 8 0 5 6 2. 0 280 5 7 12. 0 0 6 7 1. 0 180 7 6 7. 0 0

Network Model 6: Network flow for multiple products Minimum cost network flow model - Multiple Products Same network structure as before (this can easily relaxed) Shipment of 2 products (P 1 and P 2) The arc capacity represent the maximum flow for both products Note that in this case the 2 products are competing for the arc capacity Each plant has separate capacity for each product and each customer separate demand for each product

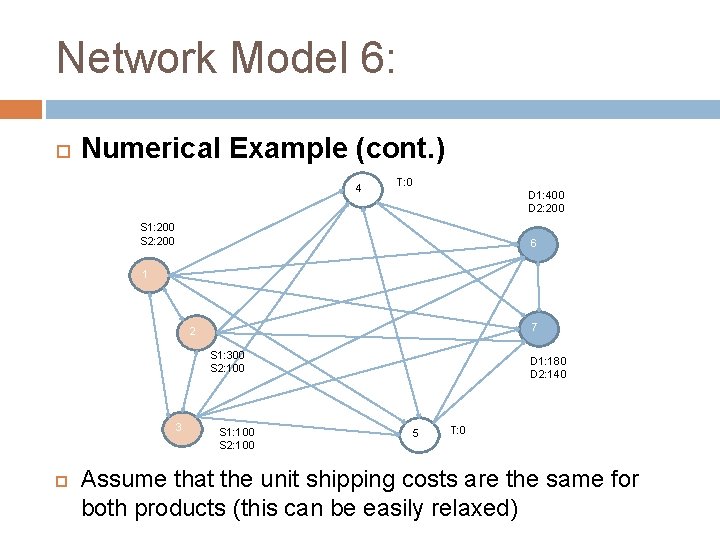
Network Model 6: Numerical Example (cont. ) 4 T: 0 D 1: 400 D 2: 200 S 1: 200 S 2: 200 6 1 7 2 S 1: 300 S 2: 100 3 S 1: 100 S 2: 100 D 1: 180 D 2: 140 5 T: 0 Assume that the unit shipping costs are the same for both products (this can be easily relaxed)

Network Model 6 Mathematical Model xijp = quantity shipped of product p from node i to node j = demand or supply of a node j, and it can be positive or negative or zero for product p = capacity of an arc ij of the network = cost of producing and shipping one unit from node i to node j subject to

Network model 6 Formulation of the model Min Z = 5 X 121+3 X 131+5 X 141+5 X 151+20 X 161+20 X 171+. . . + 1 X 671 + 7 X 761 + 5 X 122+3 X 132+5 X 142+5 X 152+20 X 162+20 X 172+. . . + 1 X 672 + 7 X 762 s. t. Node 1, P 1: (X 121 + X 131 +. . . + X 171) – (X 211 + X 311) = 200 Node 1, P 2: (X 122 + X 132 +. . . + X 172) – (X 212 + X 312) = 200 … Node 7, P 1: X 761 - (X 171 + X 271 +. . . + X 671) = - 400 Node 7, P 2: X 762 - (X 172 + X 272 +. . . + X 672) = - 200 X 121+X 122 ≤ 300 … X 761+X 762 ≤ 300 Xij 0

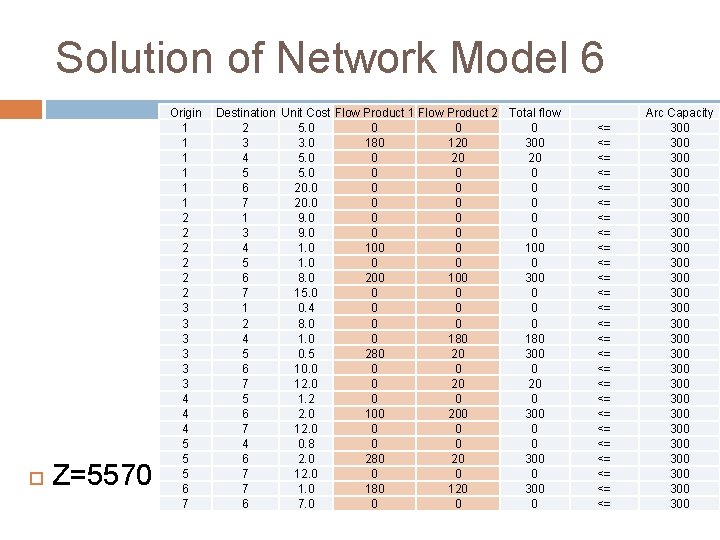
Solution of Network Model 6 Z=5570 Origin 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 7 Destination Unit Cost Flow Product 1 Flow Product 2 Total flow 2 5. 0 0 3 3. 0 180 120 300 4 5. 0 0 20 20 5 5. 0 0 6 20. 0 0 7 20. 0 0 1 9. 0 0 3 9. 0 0 4 1. 0 100 5 1. 0 0 6 8. 0 200 100 300 7 15. 0 0 1 0. 4 0 0 0 2 8. 0 0 4 1. 0 0 180 5 0. 5 280 20 300 6 10. 0 0 7 12. 0 0 20 20 5 1. 2 0 0 0 6 2. 0 100 200 300 7 12. 0 0 4 0. 8 0 0 0 6 2. 0 280 20 300 7 12. 0 0 7 1. 0 180 120 300 6 7. 0 0 <= <= <= <= <= <= <= Arc Capacity 300 300 300 300 300 300 300

Network Optimization Models and Examples cont. More enhanced Capacitated Plant Location Models Model 7: Simultaneous location of plants and warehouses Model 8: Accounting for Taxes, Tariffs, and Customer Requirements Model 9: Adding restrictions on the number of locations + alternative objective functions (see excel file “AI's Athletic. xls”) Model 10: Production and shipping through transshipment points with multiple modes of transportation + location decisions (see excel file

Network Model 7 Locating Plants and Warehouses Simultaneously

Network Model 7 Model inputs m n l t Dj Ki Sh We Fi fe chi cie cej = = = number of markets or demand points number of potential factory locations number of suppliers number of potential warehouse locations annual demand from customer j potential capacity of factory at site i supply capacity at supplier h potential warehouse capacity at site e fixed cost of locating a plant at site i fixed cost of locating a warehouse at site e cost of shipping one unit from supply source h to factory i cost of producing and shipping one unit from factory i to warehouse e = cost of shipping one unit from warehouse e to customer j

Network Model 7 Goal is to identify plant and warehouse locations and quantities shipped that minimize the total fixed and variable costs Yi Ye xej xie xhi = = = 1 if factory is located at site i, 0 otherwise 1 if warehouse is located at site e, 0 otherwise quantity shipped from warehouse e to market j quantity shipped from factory at site i to warehouse e quantity shipped from supplier h to factory at site i

Network Model 7 subject to

Network Model 8 A supply chain network should maximize profits after tariffs and taxes while meeting customer service requirements If rj is the revenue of selling one product unit to market j, then the objective and constraint are modified as:

Network Model 9 Yij Xi distij P dj = = = 1 if location i serves customer j; 0 otherwise 1 if a warehouse is located at site i, 0 otherwise distance between warehouse at site i to customer j total number of warehouses to locate demand of customer j

Network Models 9 & 10 AI’s Athletic excel file MIP network flow with multiple trans modes and location excel file

Network Optimization Models and Examples cont. Multiple products and modes of transportation? DHL Supply Chain Case Multiple products, modes of transportation + location decisions but no fixed costs? Logistics Network Design Problem see paper of Cordeau, Pasin and Solomon 2003 Multiple products, location decisions + fixed costs? Mixed Integer Non-Linear Programming (see Floudas 1995)

Making Network Design Decisions In Practice Do not underestimate the life span of facilities Do not gloss over the cultural implications Do not ignore quality-of-life issues Focus on tariffs and tax incentives when locating facilities