5 Minute Review 1 In the worst case

5 -Minute Review 1. In the worst case, how does the width produced by RT compare with the optimal width? 2. What is the idea of radial tree drawing? What is a potential problem regarding edge placements, how can it be overcome? 3. What is the worst-case area consumption of the Radial. Tree. Layout algorithm? 4. How does the Right-Heavy-HV-Layout work? Worst case area? 5. What is a motivation for Recursive Winding?

Inf-Graph. Draw: Automatic Graph Drawing Lecture 11 Planarity Reinhard von Hanxleden rvh@informatik. uni-kiel. de Most definitions are from [Di Battista Book 99]. This lecture is based in part on material kindly provided by Bettina Speckmann, Kees Wisser, Eran Geva and Matya Katz

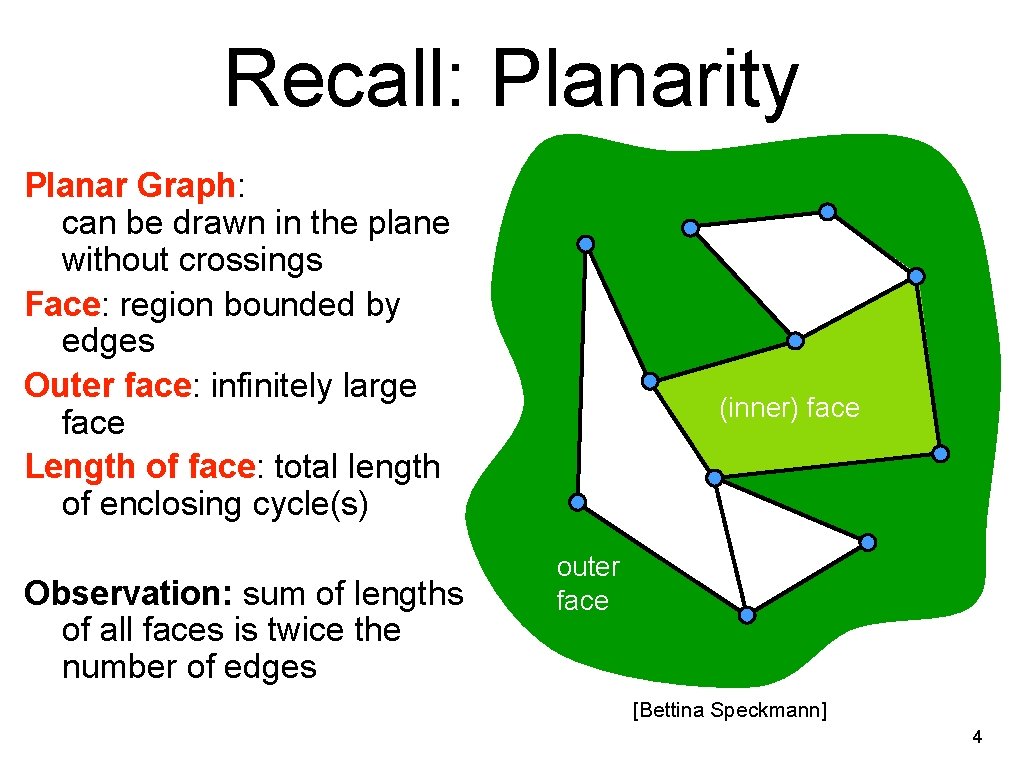
Recall: Planarity Planar Graph: can be drawn in the plane without crossings Face: region bounded by edges Outer face: infinitely large face Length of face: total length of enclosing cycle(s) Observation: sum of lengths of all faces is twice the number of edges (inner) face outer face [Bettina Speckmann] 4

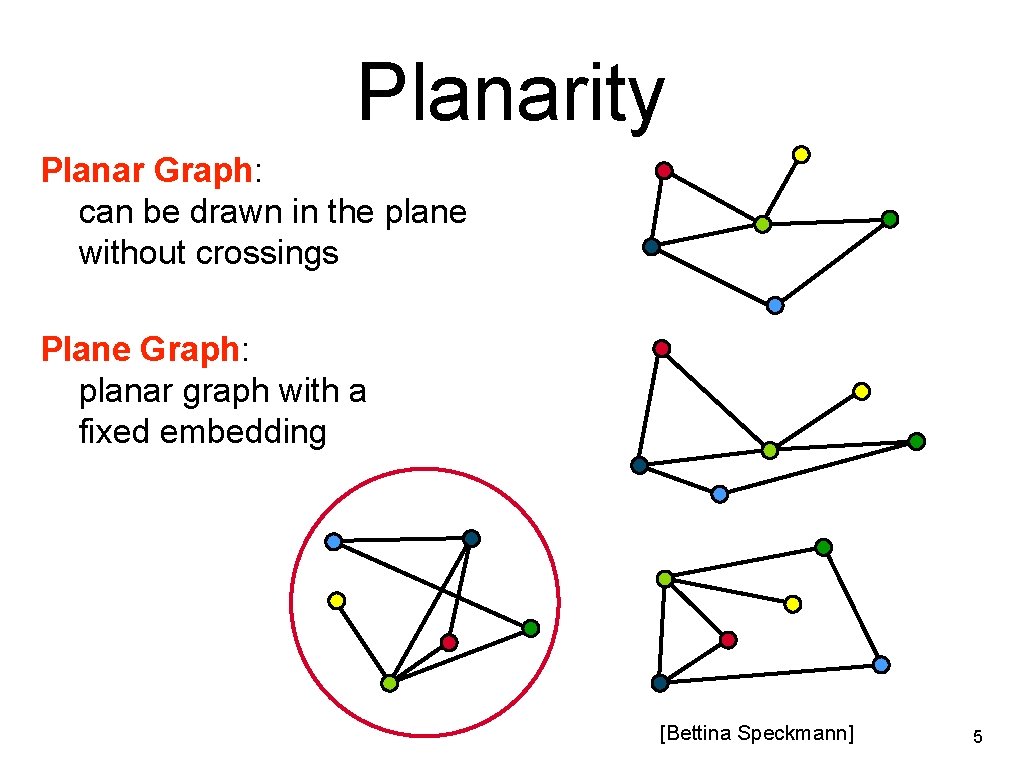
Planarity Planar Graph: can be drawn in the plane without crossings Plane Graph: planar graph with a fixed embedding [Bettina Speckmann] 5

Embeddings • Planar drawing determines circular ordering on the neighbors of each vertex v according to clockwise sequence of incident edges around v • Two planar drawings are equivalent: they determine same circular orderings of neighbor sets • (Planar/plane) embedding is equivalence class of planar drawings, described by circular order of neighbors of each vertex • Embedded graph: a graph with a specified embedding Terminology not always used consistently: • Sometimes, a (plane) embedding of G also refers to a planar drawing of G • Sometimes, plane graph also denotes a planar drawing of G 6

Planar drawings Vertices Edges points in the plane curves No edge crossings [Bettina Speckmann] 7

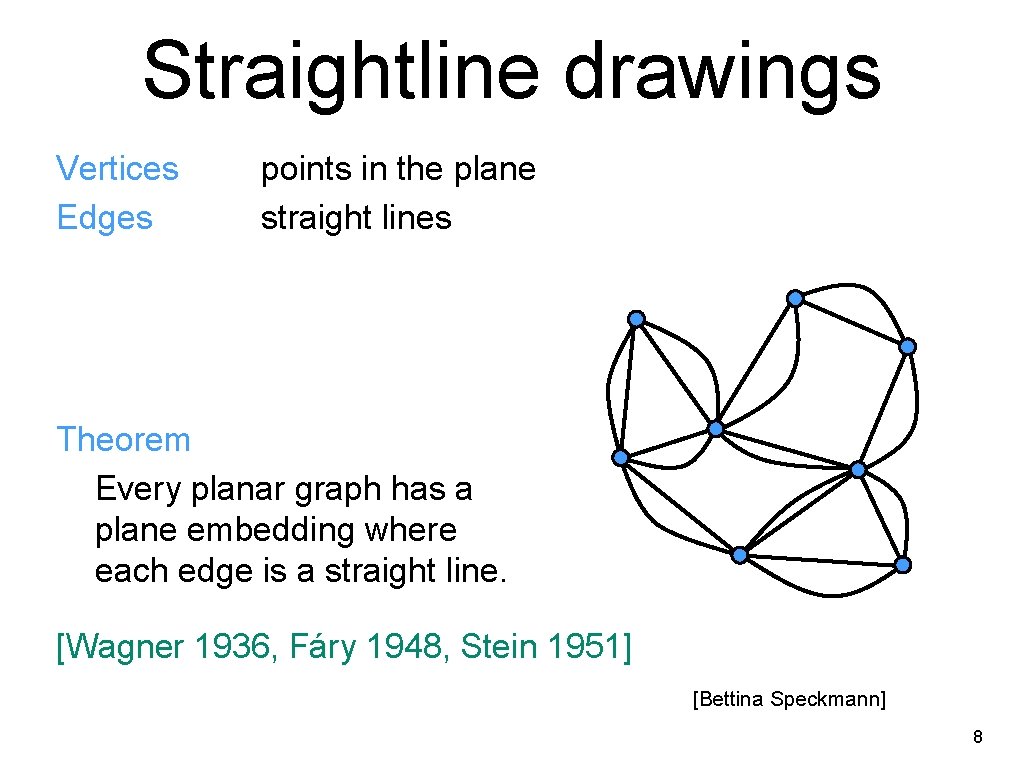
Straightline drawings Vertices Edges points in the plane straight lines Theorem Every planar graph has a plane embedding where each edge is a straight line. [Wagner 1936, Fáry 1948, Stein 1951] [Bettina Speckmann] 8

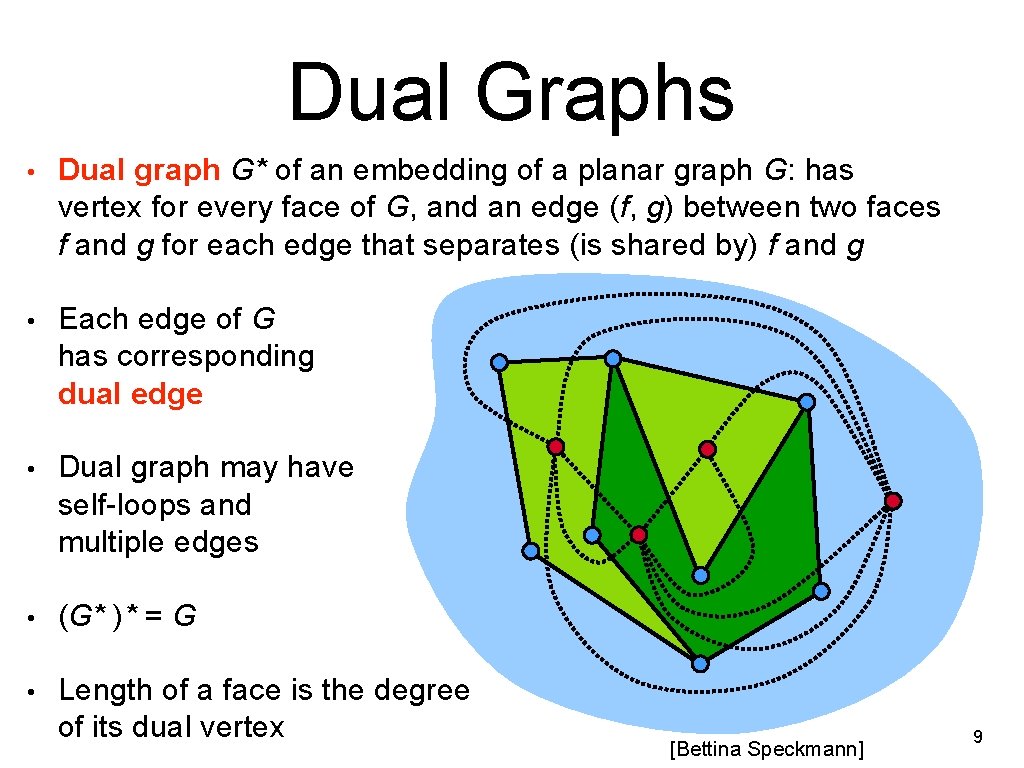
Dual Graphs • Dual graph G* of an embedding of a planar graph G: has vertex for every face of G, and an edge (f, g) between two faces f and g for each edge that separates (is shared by) f and g • Each edge of G has corresponding dual edge • Dual graph may have self-loops and multiple edges • (G* )* = G • Length of a face is the degree of its dual vertex [Bettina Speckmann] 9

Notes on Planarity • Thm: Two drawings have the same embedding iff they have the same dual graph • We say that two graphs have same topology if they have the same dual graph • We say that a layout adjustment algorithm preserves topology if the adjusted layout has the same topology as the original layout (see also mental map) 10

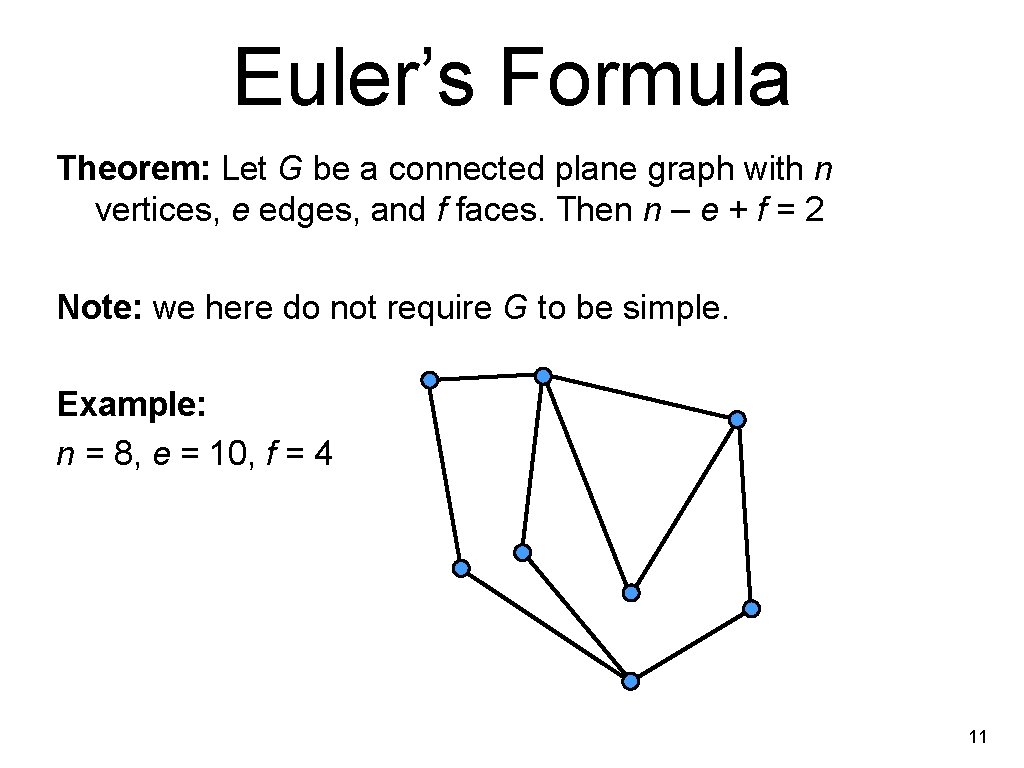
Euler’s Formula Theorem: Let G be a connected plane graph with n vertices, e edges, and f faces. Then n – e + f = 2 Note: we here do not require G to be simple. Example: n = 8, e = 10, f = 4 11

Theorem: Let G be a connected plane graph with n vertices, e edges, and f faces. Then n – e + f = 2 Proof: Induction on n. Induction base (n = 1): G is a “bouquet” of loops, each a closed curve in the embedding. If e = 0, then f = 1; formula holds. Each added loop (e++) splits a face into 2 faces (f++). Formula still holds. Thus formula holds for n = 1 for any number of edges. n=1 e=0 f=1 n=1 e=1 f=2 n=1 e=2 f=3 12

Theorem: Let G be a connected plane graph with n vertices, e edges, and f faces. Then n – e + f = 2 Proof: Induction on n. Induction step (n > 1): G is connected ⇒ can find edge e that is not a loop. When we contract e, we obtain a plane graph G’ with n’ = n – 1 vertices, e’ = e – 1 edges, and f ’ = f faces. Induction hypothesis yields n–e+f= (n’ + 1) – (e’ + 1) + f ’= n’ – e’ + f ’ = 2 ∎ For more: google „Twenty Proofs of Euler‘s Formula“ 13

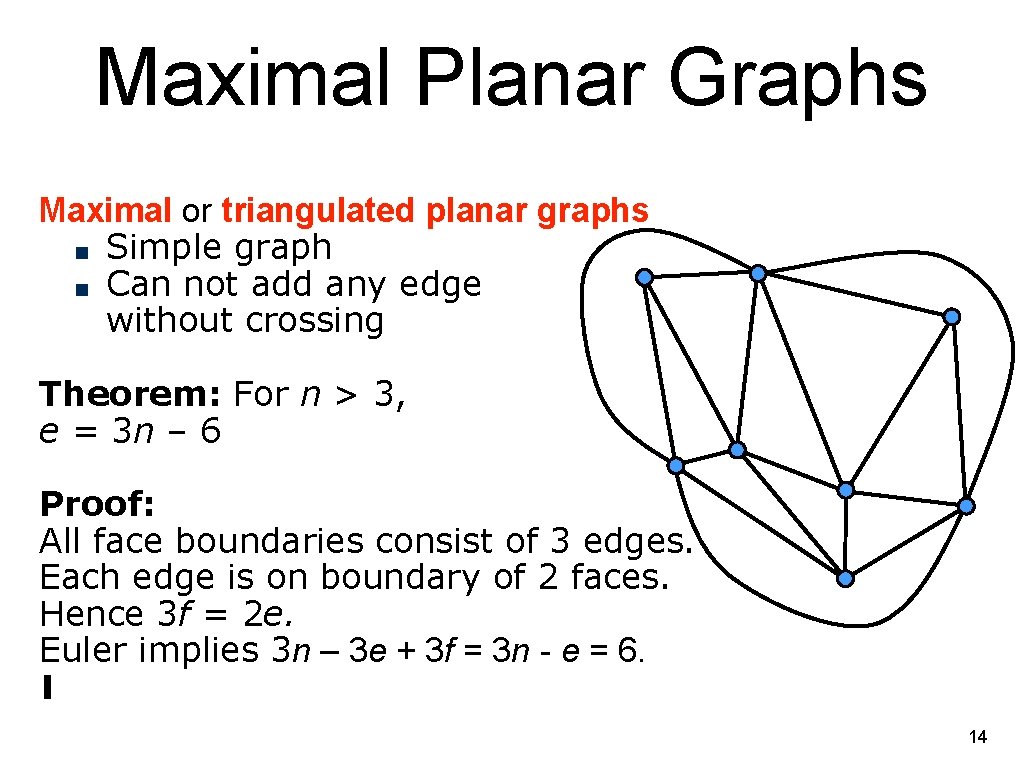
Maximal Planar Graphs Maximal or triangulated planar graphs ■ Simple graph ■ Can not add any edge without crossing Theorem: For n > 3, e = 3 n – 6 Proof: All face boundaries consist of 3 edges. Each edge is on boundary of 2 faces. Hence 3 f = 2 e. Euler implies 3 n – 3 e + 3 f = 3 n - e = 6. ∎ 14

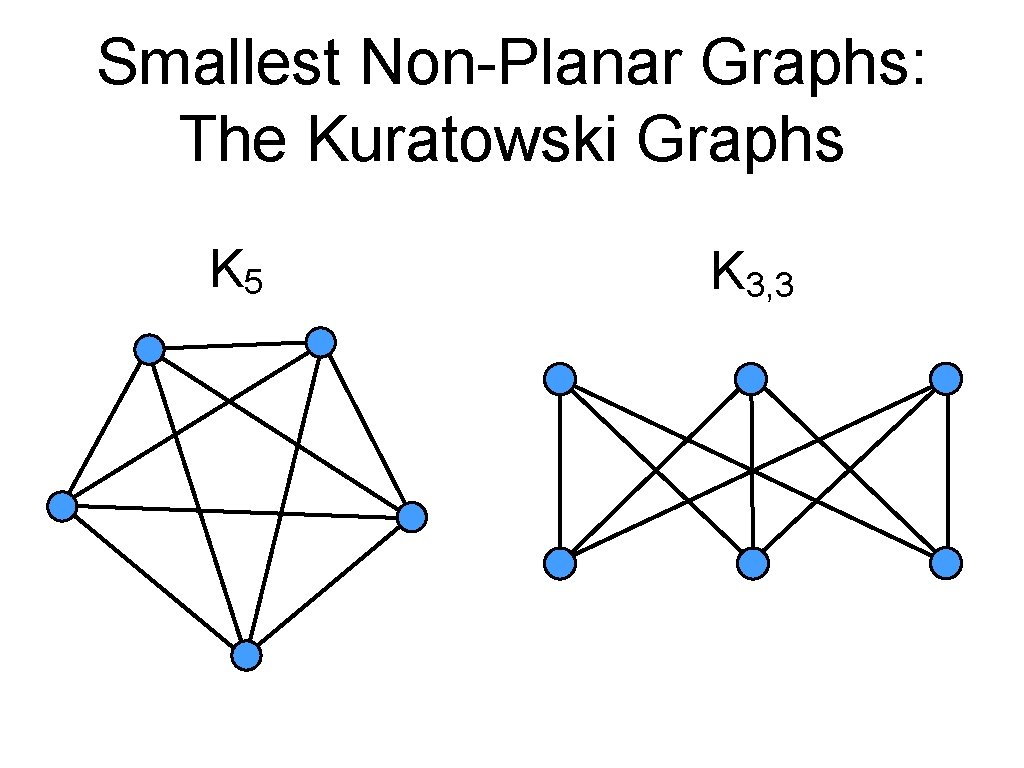
Smallest Non-Planar Graphs: The Kuratowski Graphs K 5 K 3, 3

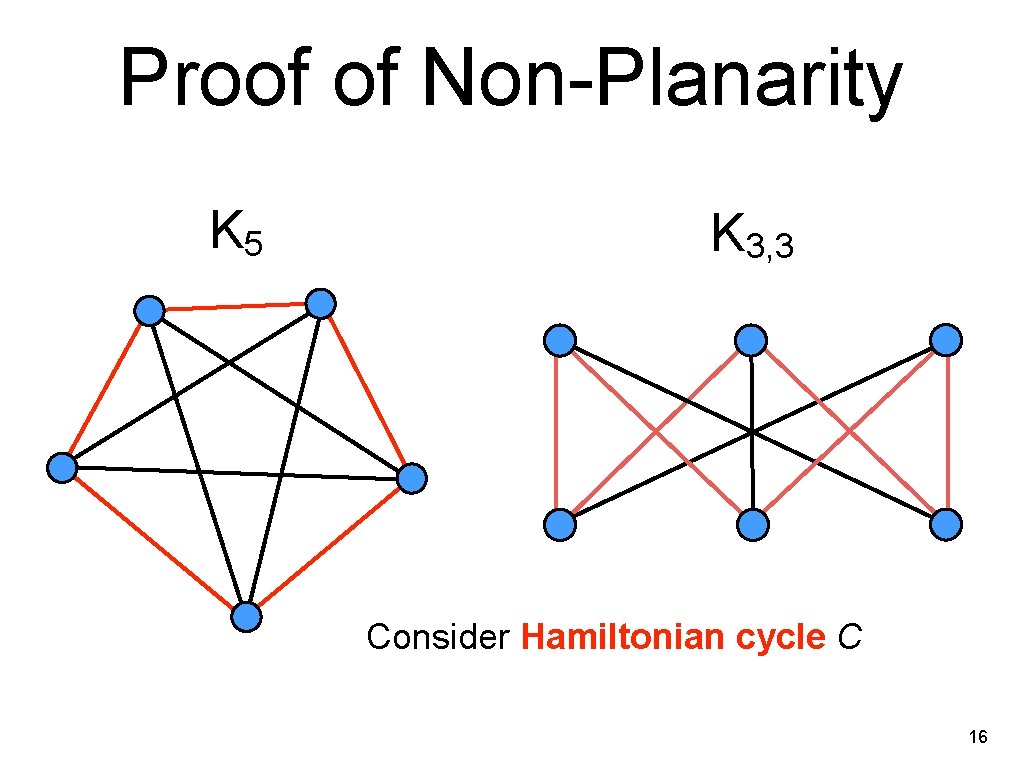
Proof of Non-Planarity K 5 K 3, 3 Consider Hamiltonian cycle C 16

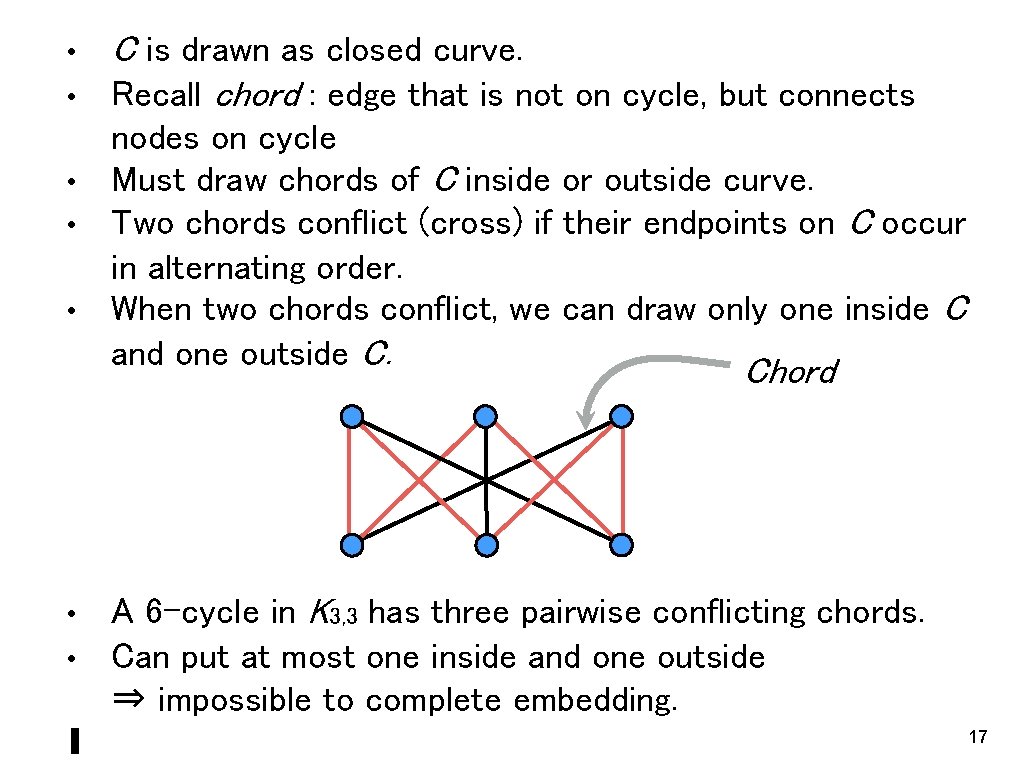
• • ∎ C is drawn as closed curve. Recall chord : edge that is not on cycle, but connects nodes on cycle Must draw chords of C inside or outside curve. Two chords conflict (cross) if their endpoints on C occur in alternating order. When two chords conflict, we can draw only one inside C and one outside C. Chord A 6 -cycle in K 3, 3 has three pairwise conflicting chords. Can put at most one inside and one outside ⇒ impossible to complete embedding. 17

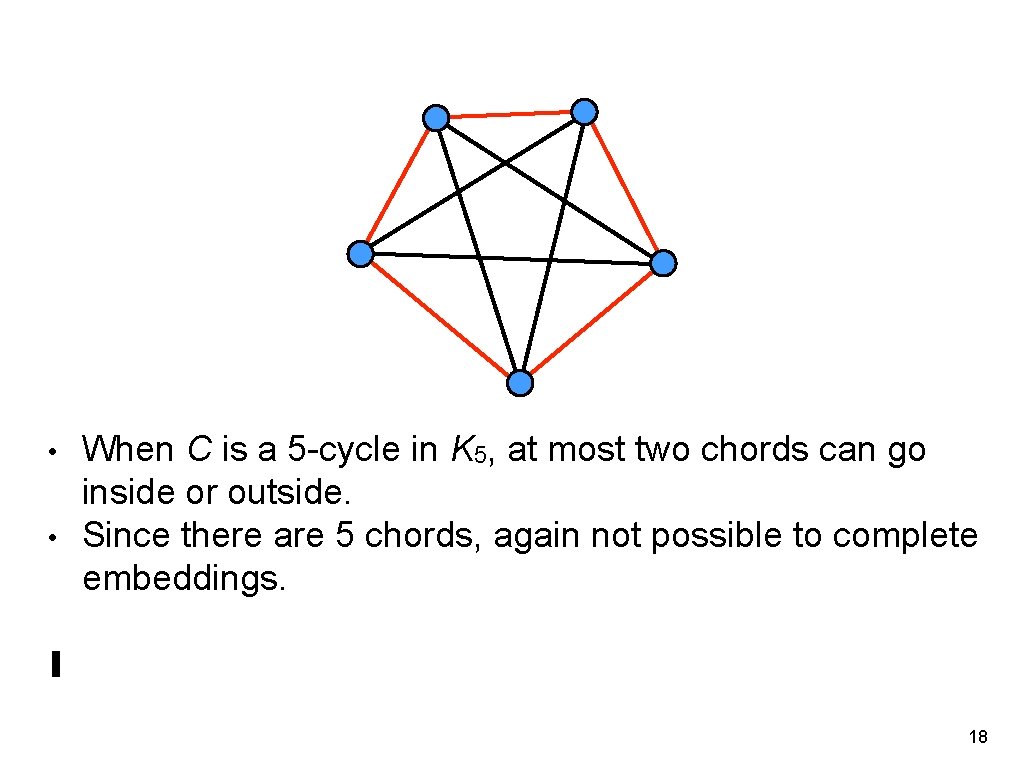
• • When C is a 5 -cycle in K 5, at most two chords can go inside or outside. Since there are 5 chords, again not possible to complete embeddings. ∎ 18

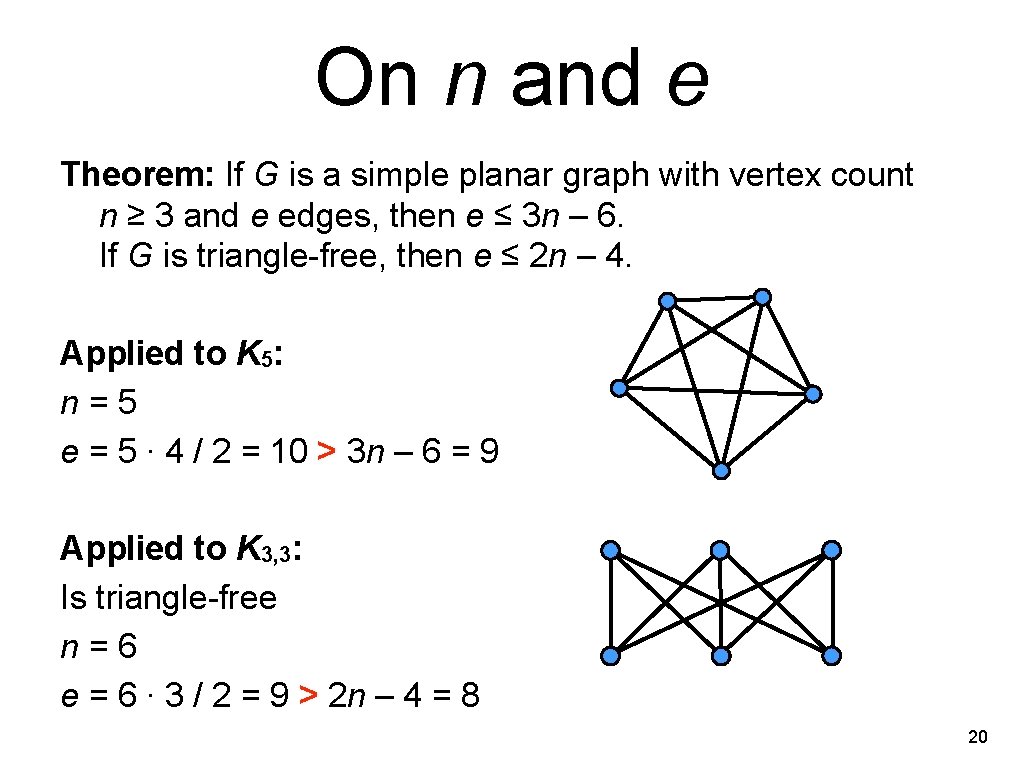
On n and e Theorem: If G is a simple planar graph with vertex count n ≥ 3 and e edges, then e ≤ 3 n – 6. If G is triangle-free, then e ≤ 2 n – 4. Proof: Suffices to consider connected graphs; otherwise could add edges. Euler: n – e + f = 2 ⇔ f = e – n + 2, with f: number of faces. n ≥ 3 ⇒ have for the length each face F: l(F) ≥ 3 Thus 2 e = Σ l(F) ≥ 3 f = 3 ∙ (e – n + 2). Thus e ≤ 3 n – 6. If G is triangle-free, then l(F) ≥ 4, thus e ≤ 2 n – 4. ∎ 19

On n and e Theorem: If G is a simple planar graph with vertex count n ≥ 3 and e edges, then e ≤ 3 n – 6. If G is triangle-free, then e ≤ 2 n – 4. Applied to K 5: n=5 e = 5 ∙ 4 / 2 = 10 > 3 n – 6 = 9 Applied to K 3, 3: Is triangle-free n=6 e = 6 ∙ 3 / 2 = 9 > 2 n – 4 = 8 20

Planarity Testing Theorem [Kuratowski 1930 / Wagner 1937] A graph G is planar if and only if it does not contain K 5 or K 3, 3 as a minor. In the following, present a simple O(n 3) planarity testing algorithm, due to [Auslander and Parter 1961], [Goldstein 1963] and [Shirly 1969], based in part on Sec. 3. 3 of [Di Battista at al. 99] and material kindly provided by Eran Geva and Matya Katz. 21

Planarity Testing • Graph is planar iff all its connected components are planar • Graph is planar iff all its biconnected components are planar • Thus preprocess G into biconnected components – the problem is restricted to biconnected graphs 22

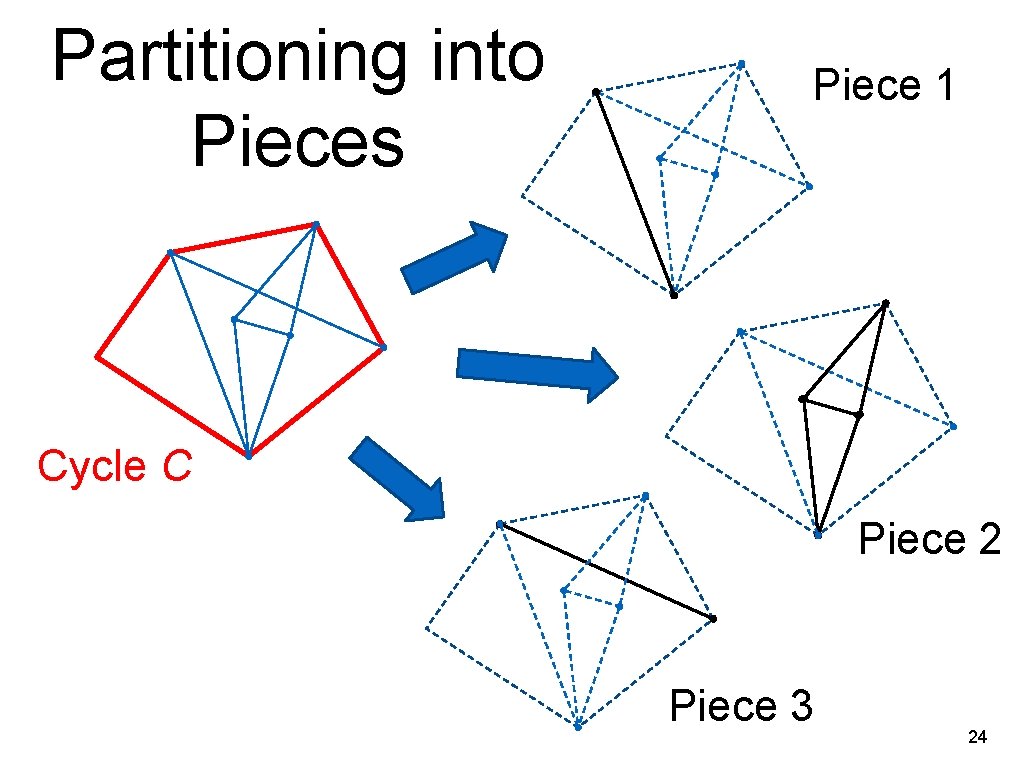
Partitioning into Pieces • Let G be biconnected. Thus G must contain a cycle, let C be a cycle in G • Classify each edge of G not on C: if 2 edges have a path between them with no vertex of C, they have the same class. • Subgraph induced by edges in a class is called a piece of G. 23

Partitioning into Pieces Piece 1 Cycle C Piece 2 Piece 3 24

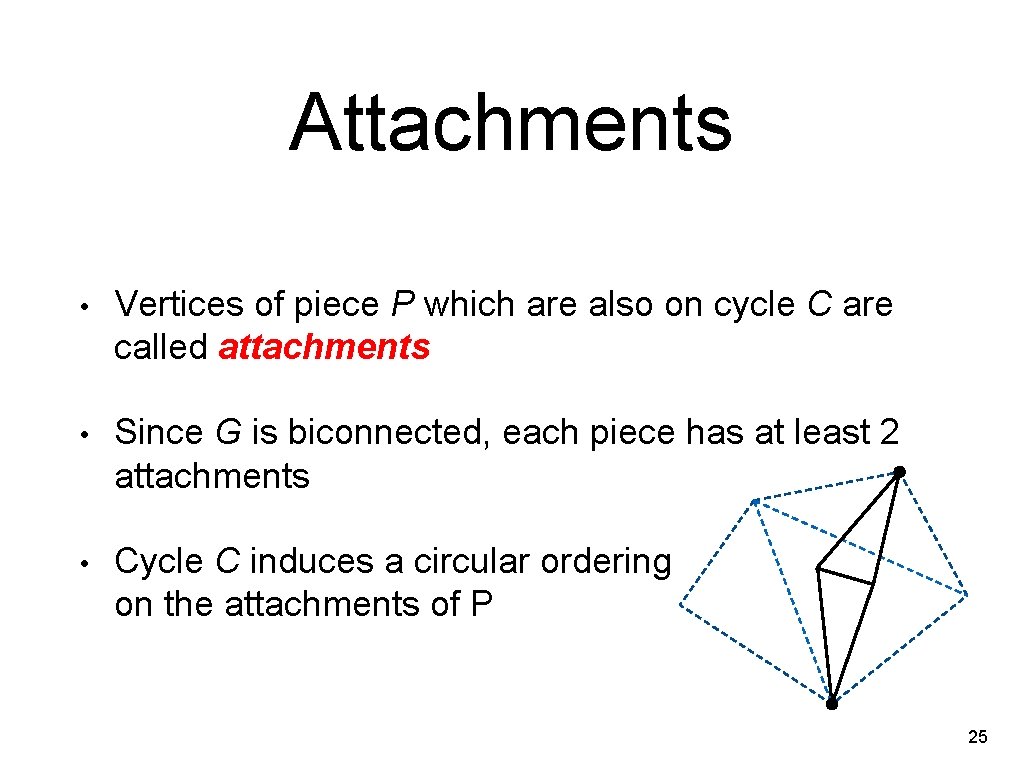
Attachments • Vertices of piece P which are also on cycle C are called attachments • Since G is biconnected, each piece has at least 2 attachments • Cycle C induces a circular ordering on the attachments of P 25

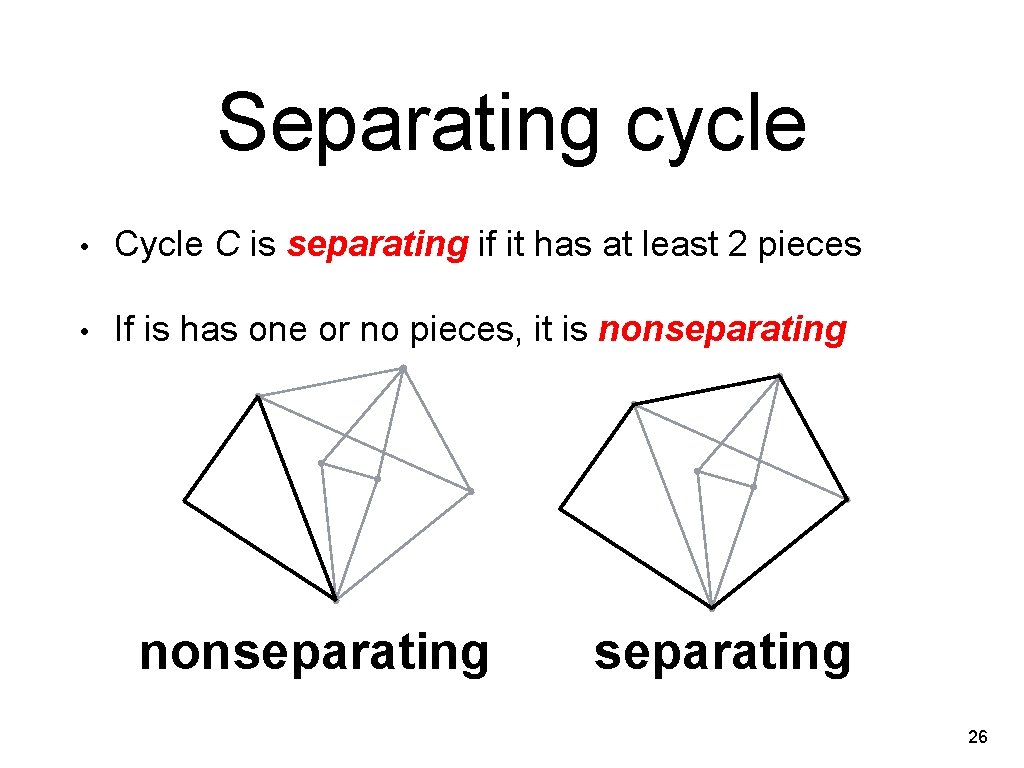
Separating cycle • Cycle C is separating if it has at least 2 pieces • If is has one or no pieces, it is nonseparating 26

Lemma 3. 4 Given: biconnected graph G, with nonseparating cycle C, piece P of C Lemma 3. 4: If P is not a path, then G has a separating cycle C’ consisting of subpath of C and a path of P Consequence: If G does not have a separating cycle, then G is planar: G then has either no cycles, or only nonseparating cycles where any piece must be a path. Lemma numbering from [Di Battista at al. 99] 27

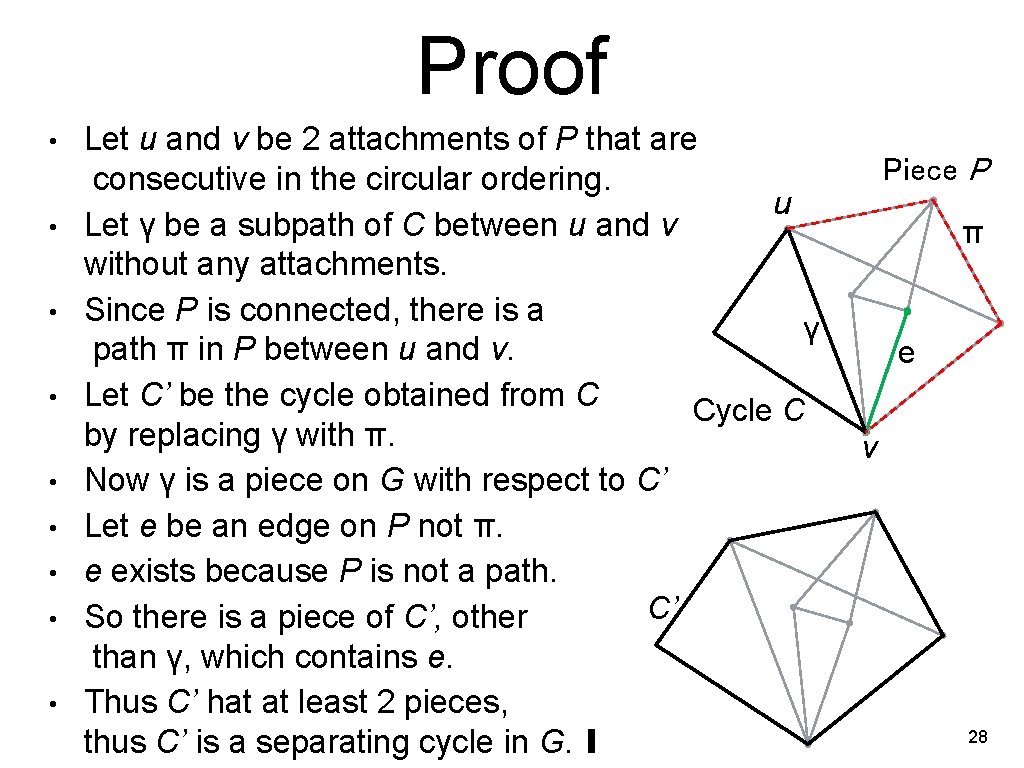
Proof • • • Let u and v be 2 attachments of P that are consecutive in the circular ordering. u Let γ be a subpath of C between u and v without any attachments. Since P is connected, there is a γ path π in P between u and v. Let C’ be the cycle obtained from C Cycle C by replacing γ with π. Now γ is a piece on G with respect to C’ Let e be an edge on P not π. e exists because P is not a path. C’ So there is a piece of C’, other than γ, which contains e. Thus C’ hat at least 2 pieces, thus C’ is a separating cycle in G. ∎ Piece P π e v 28

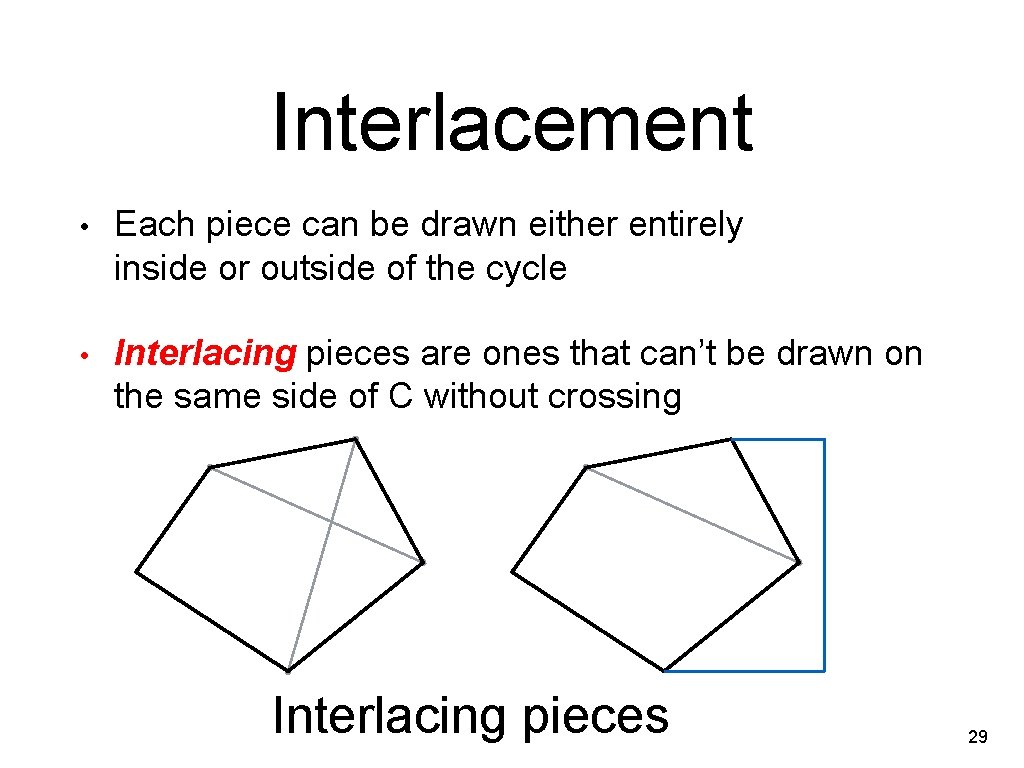
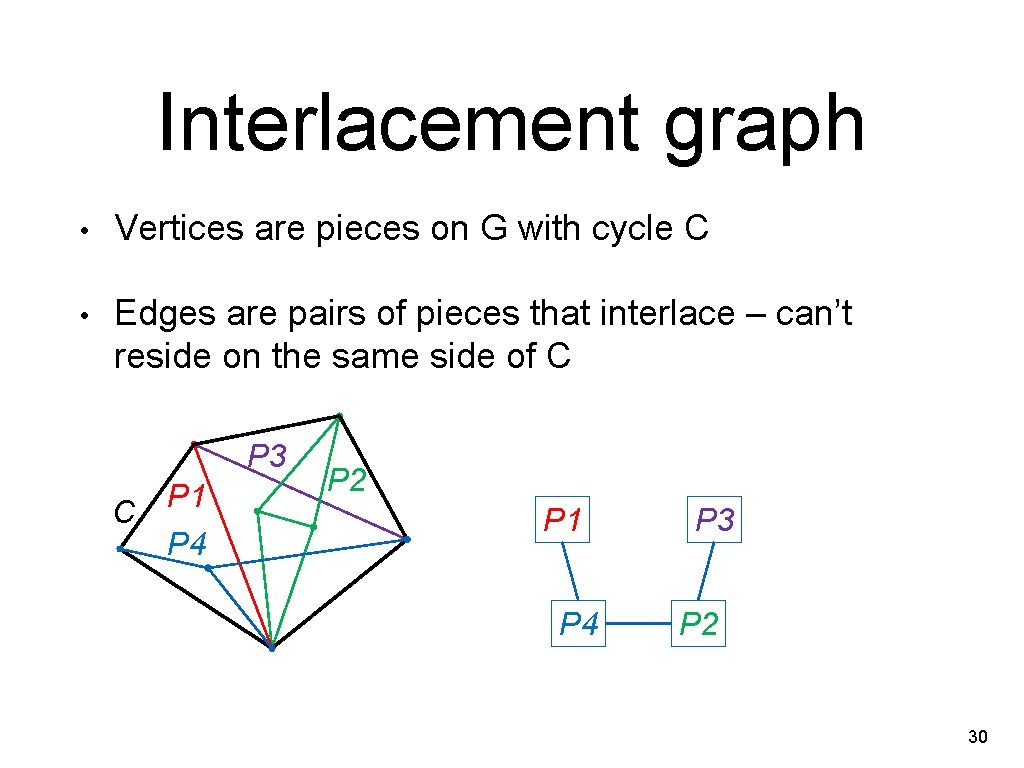
Interlacement • Each piece can be drawn either entirely inside or outside of the cycle • Interlacing pieces are ones that can’t be drawn on the same side of C without crossing Interlacing pieces 29

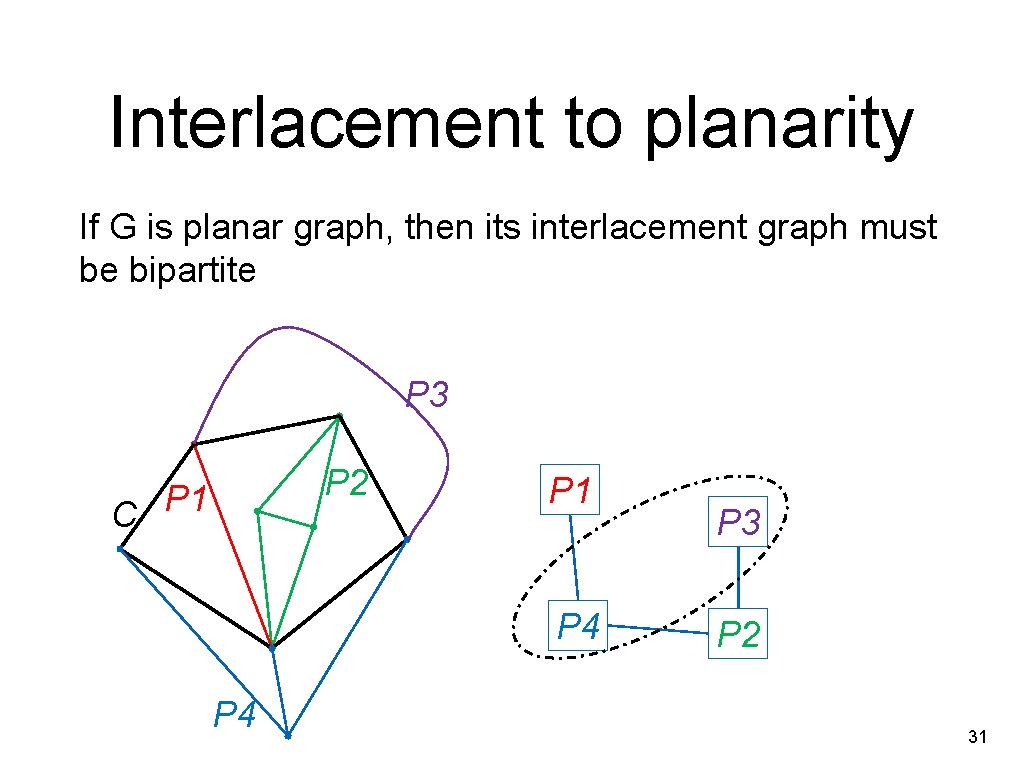
Interlacement graph • Vertices are pieces on G with cycle C • Edges are pairs of pieces that interlace – can’t reside on the same side of C P 3 P 1 C P 4 P 2 P 1 P 4 P 3 P 2 30

Interlacement to planarity If G is planar graph, then its interlacement graph must be bipartite P 3 P 2 P 1 C P 1 P 4 P 3 P 2 31

Theorem 3. 8 A biconnected graph G with cycle C is planar iff • For each piece P, graph obtained by adding P to C is planar, and • The interlacement graph of pieces of G with cycle C is bipartite 32

Planarity Testing Input: biconnected graph G Output: indication whether G is planar 1. Check Euler's formula (e ≤ 3 n – 6). If it is not fulfilled: return „nonplanar“ 2. Find separating cycle C of G. If none exists: return „planar“ (recall Lemma 3. 4) 3. For each piece P of C that is not a path, test planarity of P by recursion, possibly returning “nonplanar” 4. Compute interlacement graph of the pieces 5. If interlacement graph is not bipartite: return „nonplanar“ 6. Return „planar" 33

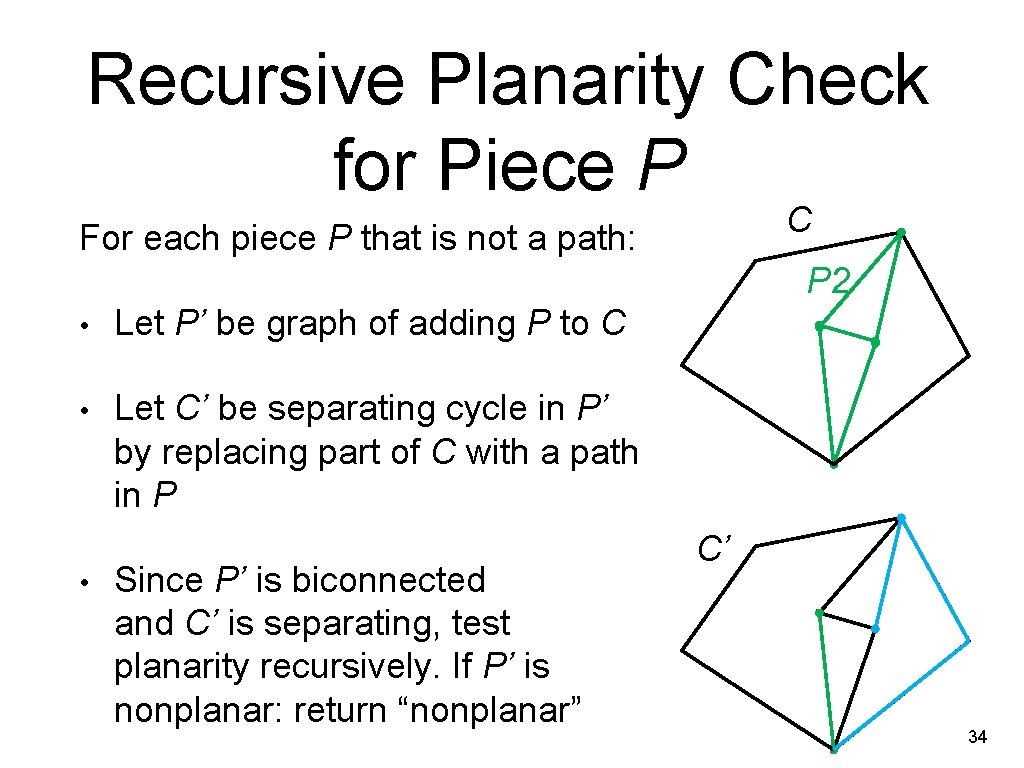
Recursive Planarity Check for Piece P C For each piece P that is not a path: P 2 • Let P’ be graph of adding P to C • Let C’ be separating cycle in P’ by replacing part of C with a path in P • Since P’ is biconnected and C’ is separating, test planarity recursively. If P’ is nonplanar: return “nonplanar” C’ 34

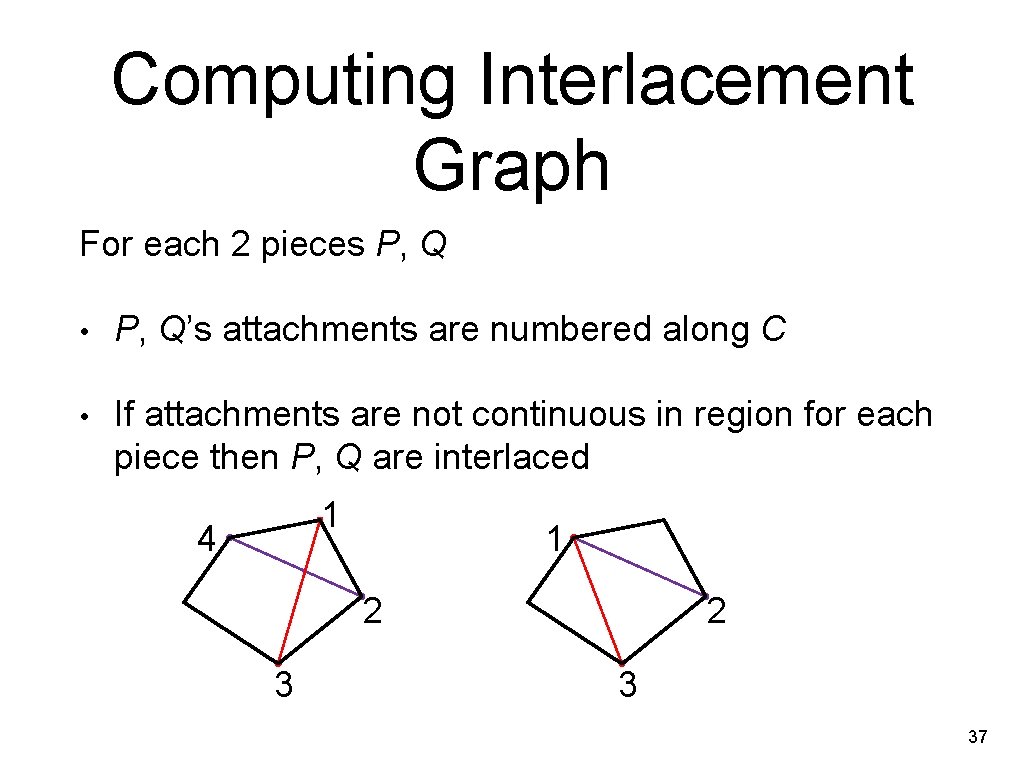
Computing Interlacement Graph For each 2 pieces P, Q • P, Q’s attachments are numbered along C • If attachments are not continuous in region for each piece then P, Q are interlaced 1 4 1 2 3 37

Computing Interlacement Graph – Complexity • Checking whether one piece conflicts with any other takes O(n) • Checking all pieces for conflicts takes O(n 2) • Resulting interlacement graph has O(n) vertices and O(n 2) edges • Checking if it’s bipartite takes O(n 2) (See book for details) 38

Overall Runtime • Each recursive invocation takes O(n 2) • Each recursion removes at least one edge of G • There are O(n) edges • Runtime is O(n 3), including time for checking Euler’s formula and finding separating cycle 39

Conclusions • Inspired by this, [Hopcroft and Tarjan 74] developed planarity testing that runs in O(n) time • Can also test in O(n) time whether a directed graph permits an upward representation. • However, testing whether a graph permits an upward planar representation is NP complete [Garg and Tamassia, 1995] 40