5 Minute Review 1 How does the Inorder

5 -Minute Review 1. How does the Inorder tree layout algorithm work? Which tree drawing requirements does it (not) fulfill? What is its main drawback? 2. How does the algorithm by Whetherell and Shannon (WS) work? How efficient is it, why? Drawbacks? 3. Are isomorphy preservation and minimum width always compatible with each other? 4. Compared to WS, what is the advantage of the algorithm by Reingold and Tilford (RT)? What is its complexity? 5. What is a simple radial layout algorithm? What is a possible hitch with it, how can that be avoided? 1

Inf-Graph. Draw: Automatic Graph Drawing Lecture 9 Series-Parallel Digraphs Reinhard von Hanxleden rvh@informatik. uni-kiel. de This lecture is based in part on material kindly provided by Eran Geva and Matya Katz 2

Series-Parallel (SP) Digraphs Directed graph with a source and sink nodes Source and sink are called poles Defined recursively sink Assume simple graph, source thus no multiple edges • SP digraphs are planar • Base case: An edge with source and sink vertices • • [Di Battista et al. book ‘ 99, Sec. 3. 2] Bertolazzi, Cohen, Di Battista, Tamassia, Tollis, How to Draw a Series. Parallel Digraph, SWAT ’ 92, LNCS vol. 621

Series composition of digraphs Identify sink of one and source of other as one vertex t 2 t 1 G 1 s 1 t’ 2 + G 2 s 2 G 2 = t 1 G 1 s 1

Parallel composition of digraphs Identify as one vertex both their sources Identify as one vertex both their sinks t 1 + G 1 s 1 t 2 G 2 s 2 = G 1 G 2 s 1

Decomposition trees • • Associate SP digraph with parse tree T Binary tree Consists of S-nodes, P-nodes and Q-nodes Defined recursively

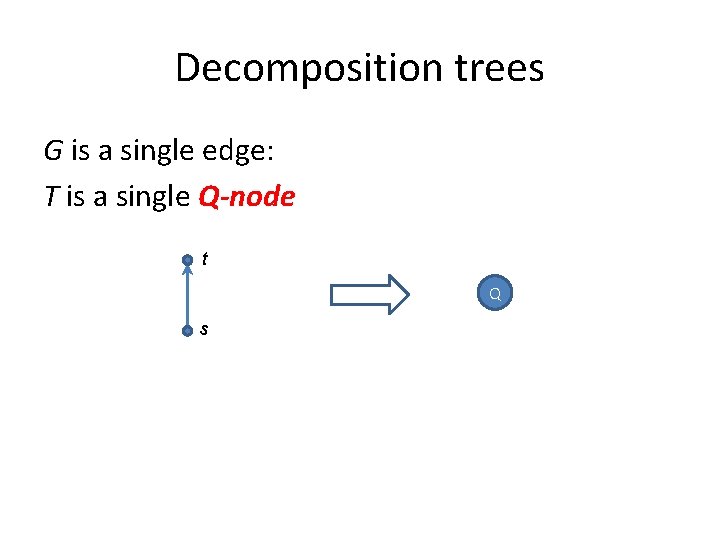
Decomposition trees G is a single edge: T is a single Q-node t Q s

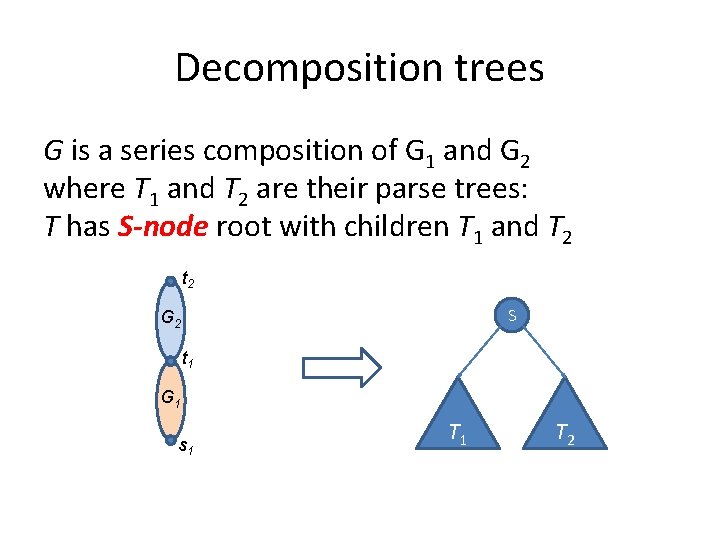
Decomposition trees G is a series composition of G 1 and G 2 where T 1 and T 2 are their parse trees: T has S-node root with children T 1 and T 2 t 2 S G 2 t 1 G 1 s 1 T 2

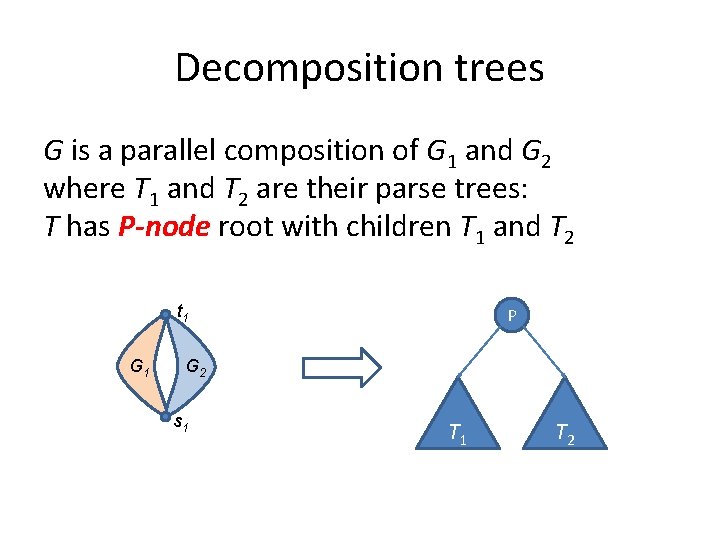
Decomposition trees G is a parallel composition of G 1 and G 2 where T 1 and T 2 are their parse trees: T has P-node root with children T 1 and T 2 t 1 G 1 P G 2 s 1 T 2

Decomposition trees • If a node has the same type as his parent, make it the right child • Then T is unique for G • If G has n nodes, then T has O(n) nodes • T can be created in O(n) time, so will be assumed to be part of the input

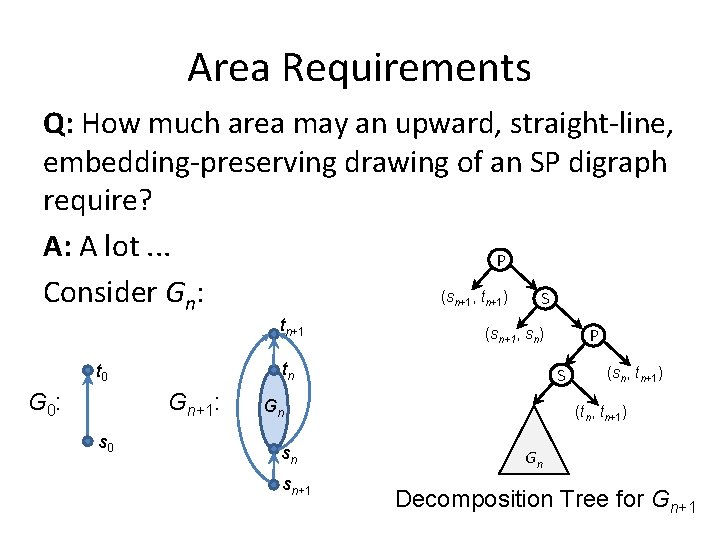
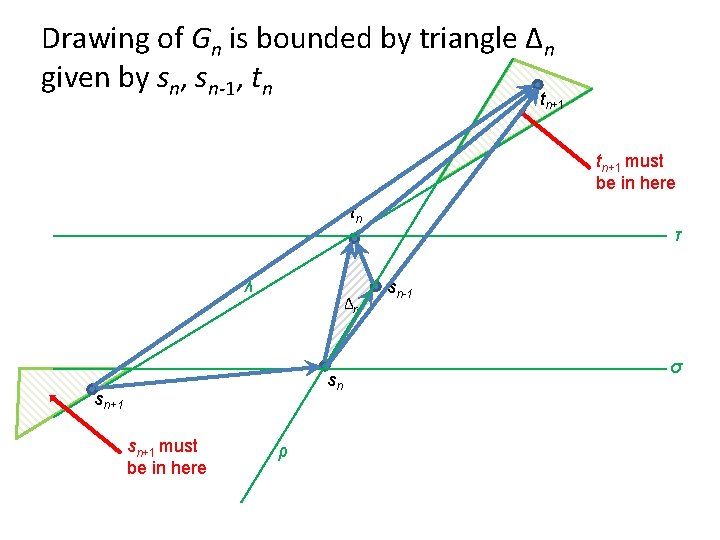
Area Requirements Q: How much area may an upward, straight-line, embedding-preserving drawing of an SP digraph require? A: A lot. . . P (s , t ) Consider Gn: S n+1 tn+1 Gn+1: s 0 S Gn sn sn+1 P (sn+1, sn) tn t 0 G 0: n+1 (sn, tn+1) (tn, tn+1) Gn Decomposition Tree for Gn+1

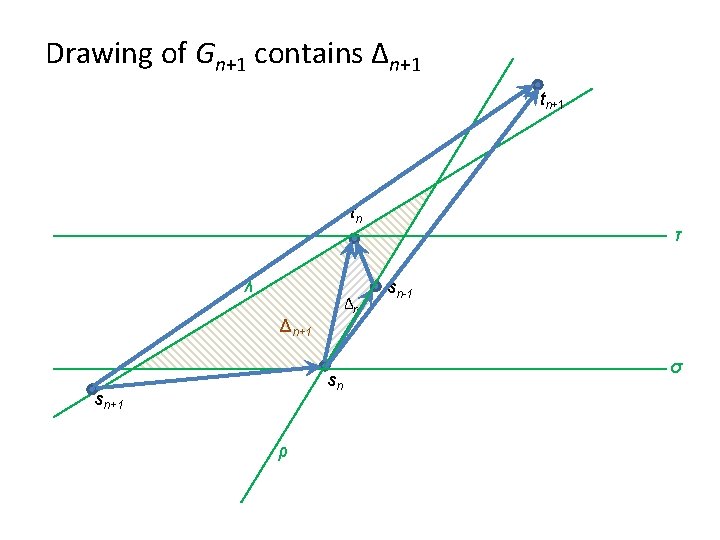
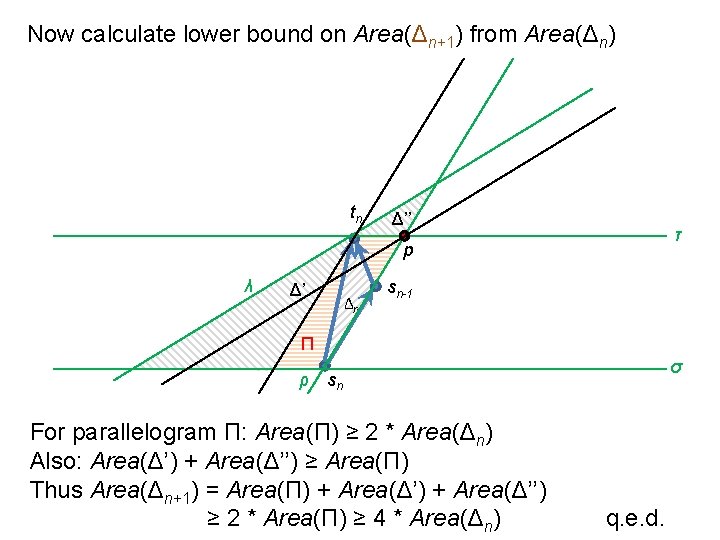
Area Requirements Theorem [Bertolazzi et al. ‘ 92]: An upward, embedding-preserving, straight-line drawing of Gn requires area Ω(4 n), under any resolution rule. Resolution rule: e. g. , • minimum separation between two nodes • integer coordinates Proof: We show that Area(Gn+1) ≥ 4 * Area(Gn).

Drawing of Gn is bounded by triangle Δn given by sn, sn-1, tn tn+1 must be in here tn λ Δn sn sn+1 must be in here ρ τ sn-1 σ

Drawing of Gn+1 contains Δn+1 tn λ Δn Δn+1 sn sn+1 ρ τ sn-1 σ

Now calculate lower bound on Area(Δn+1) from Area(Δn) tn Δ’’ τ p λ Δ’ Δn sn-1 Π ρ σ sn For parallelogram Π: Area(Π) ≥ 2 * Area(Δn) Also: Area(Δ’) + Area(Δ’’) ≥ Area(Π) Thus Area(Δn+1) = Area(Π) + Area(Δ’’) ≥ 2 * Area(Π) ≥ 4 * Area(Δn) q. e. d.

Right-pushed embedding • (u, v) is transitive in G if there is another path from u to v • As pre-processing to Δ-SP-Draw, modify embedding into right-pushed embedding: transitive edge (u, v) is on the right of all components with u and v poles • This permits O(n 2) drawing area

Δ-SP-Draw • Produces upward embedding of SP-digraph • Drawing inside a bounding triangle Δ(Γ) which is isosceles (gleichschenklig) and right-handed • Series – place one above the other • Parallel – place one to the right of the other

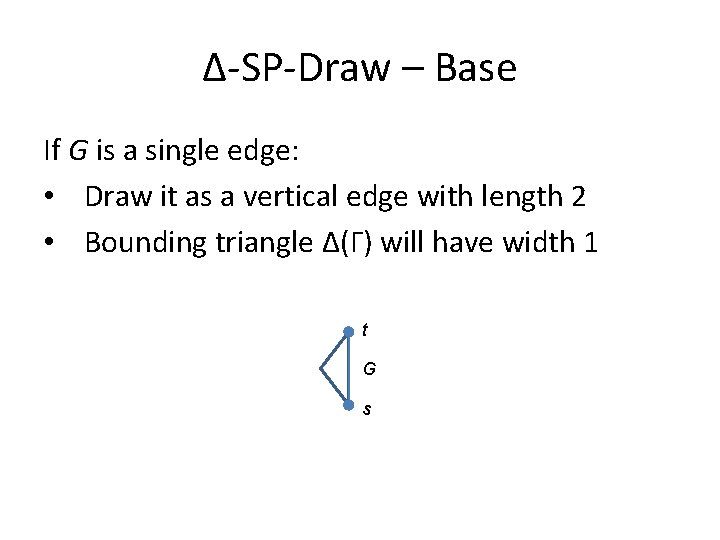
Δ-SP-Draw – Base If G is a single edge: • Draw it as a vertical edge with length 2 • Bounding triangle Δ(Γ) will have width 1 t G s

Δ-SP-Draw – Series If G is a series composition of G 1 and G 2: • Recursively draw Γ 1 and Γ 2 • Translate Γ 2 so G 1’s sink is on G 2’s source • Extend bounding triangle Δ(Γ) accordingly Note: sources differ on whether G 1 is placed above or below G 2. We here stick to the order of the original paper, which places G 1 below G 2 (and calls them G’ and G’’). G 2 G 1

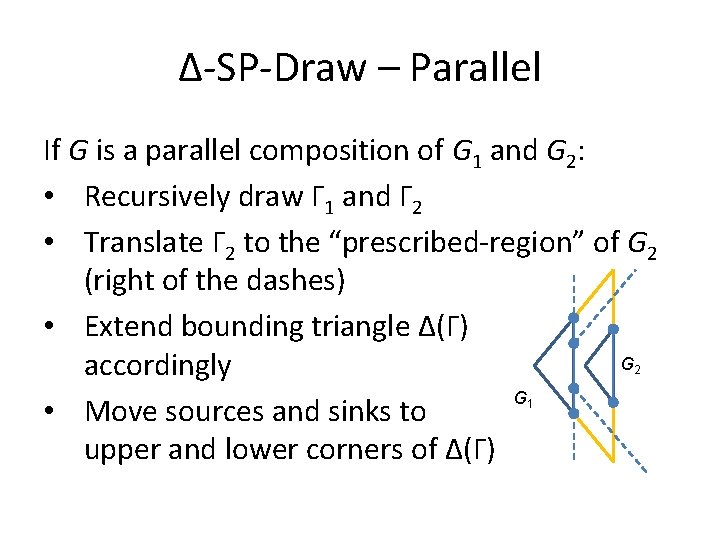
Δ-SP-Draw – Parallel If G is a parallel composition of G 1 and G 2: • Recursively draw Γ 1 and Γ 2 • Translate Γ 2 to the “prescribed-region” of G 2 (right of the dashes) • Extend bounding triangle Δ(Γ) G accordingly G • Move sources and sinks to upper and lower corners of Δ(Γ) 2 1

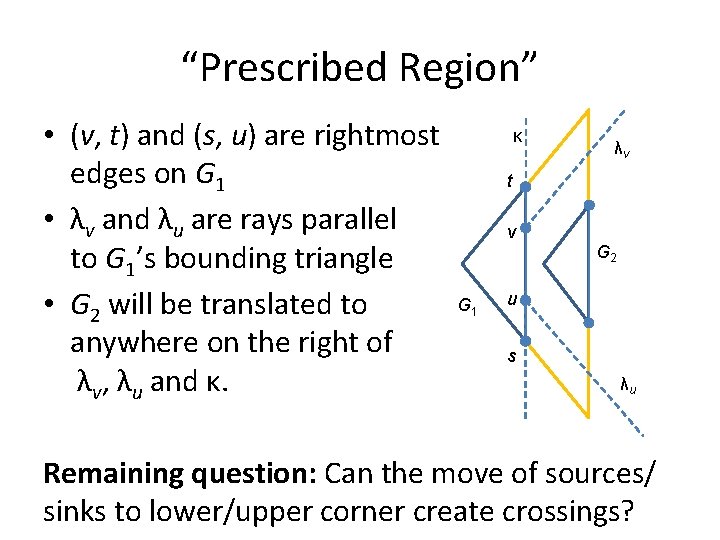
“Prescribed Region” • (v, t) and (s, u) are rightmost edges on G 1 • λv and λu are rays parallel to G 1’s bounding triangle • G 2 will be translated to anywhere on the right of λv, λu and κ. κ λv t v G 1 G 2 u s λu Remaining question: Can the move of sources/ sinks to lower/upper corner create crossings?

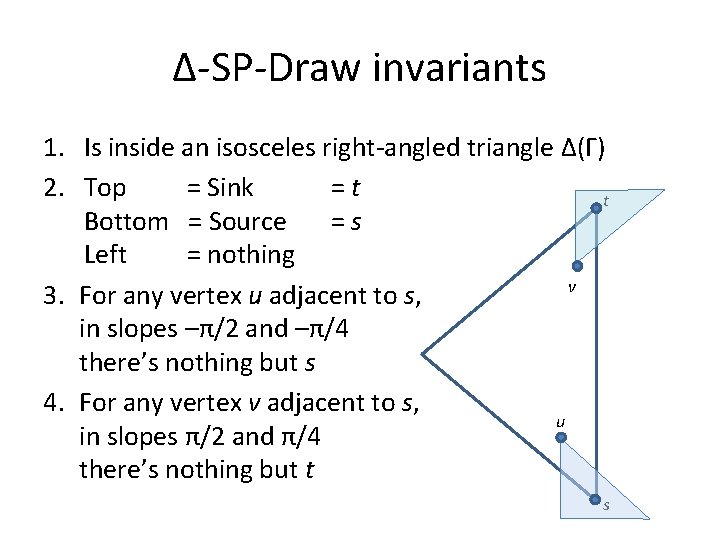
Δ-SP-Draw invariants 1. Is inside an isosceles right-angled triangle Δ(Γ) 2. Top = Sink =t t Bottom = Source =s Left = nothing v 3. For any vertex u adjacent to s, in slopes –π/2 and –π/4 there’s nothing but s 4. For any vertex v adjacent to s, u in slopes π/2 and π/4 there’s nothing but t s

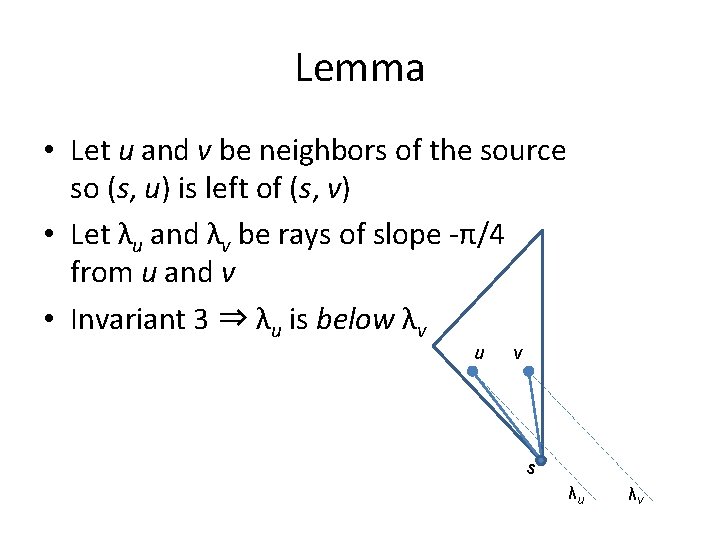
Lemma • Let u and v be neighbors of the source so (s, u) is left of (s, v) • Let λu and λv be rays of slope -π/4 from u and v • Invariant 3 ⇒ λu is below λv u v s λu λv

Consequence of Lemma If G 2 is placed to the right of G 1 and above λu where (s, u) is the rightmost edge of s on G 1: • No vertex of G 2 is in the wedge limited by the –π/4 ray from the neighbors of s • Hence, if invariant 3 is held on u G 1 and G 2, it is also held on G Symmetrically invariant 4 can be proved s

Therefore: • Proving Invariants 3 and 4 guarantee that s and t can be moved as described in the algorithm without creating crossings. • Invariant 2 states that left corner of Δ(Γ) is always empty, so G 2’s left corner can be on the base of G 1.

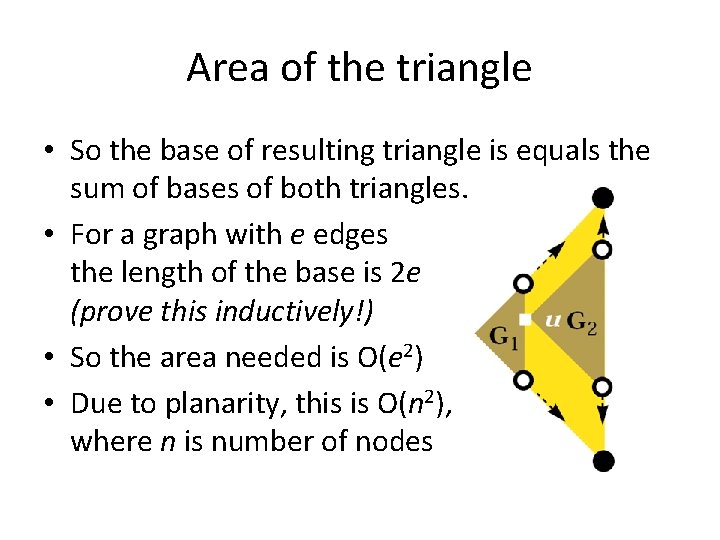
Area of the triangle • So the base of resulting triangle is equals the sum of bases of both triangles. • For a graph with e edges the length of the base is 2 e (prove this inductively!) • So the area needed is O(e 2) • Due to planarity, this is O(n 2), where n is number of nodes

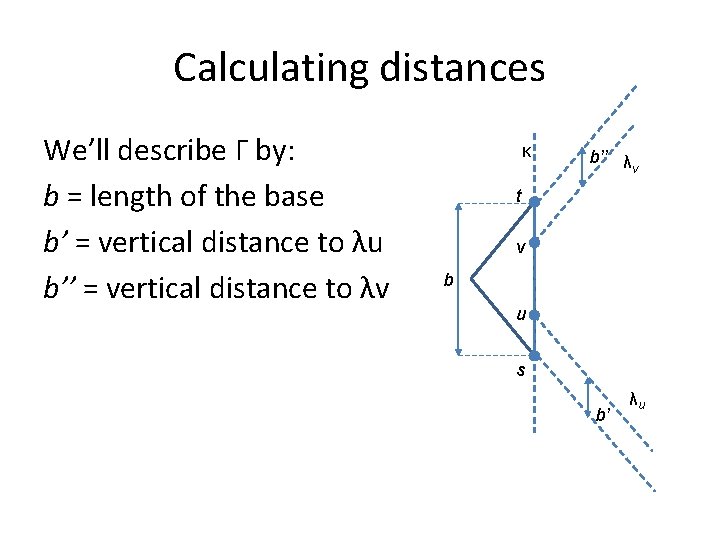
Calculating distances We’ll describe Γ by: b = length of the base b’ = vertical distance to λu b’’ = vertical distance to λv κ b’’ λ v t v b u s b’ λu

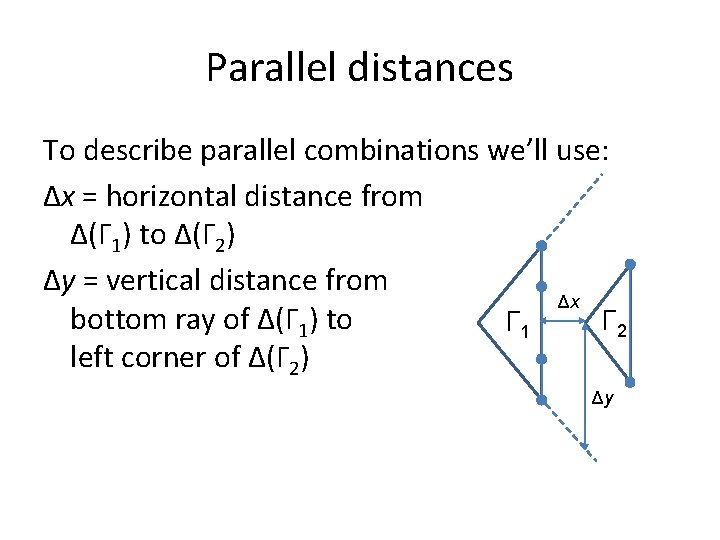
Parallel distances To describe parallel combinations we’ll use: Δx = horizontal distance from Δ(Γ 1) to Δ(Γ 2) Δy = vertical distance from Δx bottom ray of Δ(Γ 1) to Γ 2 Γ 1 left corner of Δ(Γ 2) Δy

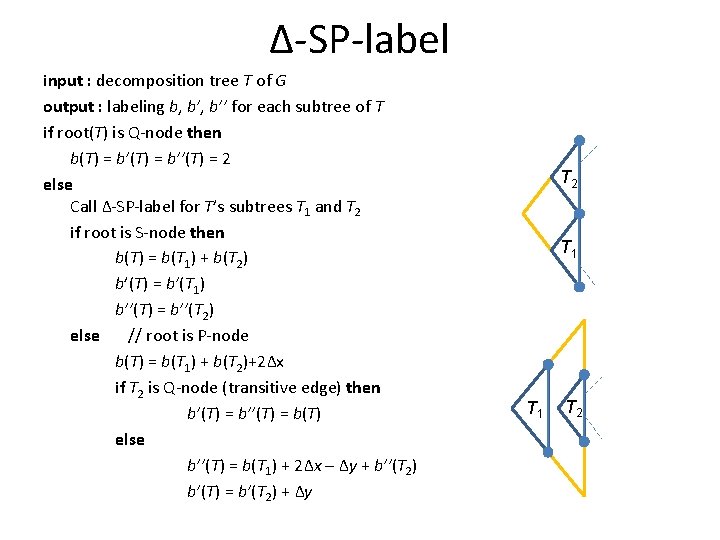
Δ-SP-label input : decomposition tree T of G output : labeling b, b’’ for each subtree of T if root(T) is Q-node then b(T) = b’’(T) = 2 else Call Δ-SP-label for T’s subtrees T 1 and T 2 if root is S-node then b(T) = b(T 1) + b(T 2) b’(T) = b’(T 1) b’’(T) = b’’(T 2) else // root is P-node b(T) = b(T 1) + b(T 2)+2Δx if T 2 is Q-node (transitive edge) then b’(T) = b’’(T) = b(T) else b’’(T) = b(T 1) + 2Δx – Δy + b’’(T 2) b’(T) = b’(T 2) + Δy T 2 T 1 T 2

Δ-SP-label • • Δx can be 0 Δy can be b’(T 1) The area needed is O(n 2) The algorithm runs in O(n) and needs O(n) space

Summary • SP Digraphs are planar graphs, defined recursively by serial and parallel decomposition • Embedding preserving, straightline, upward drawing may require exponential area • Δ-SP drawing by Bertolazzi et al. changes embedding and achieves quadratic area, runs in linear time