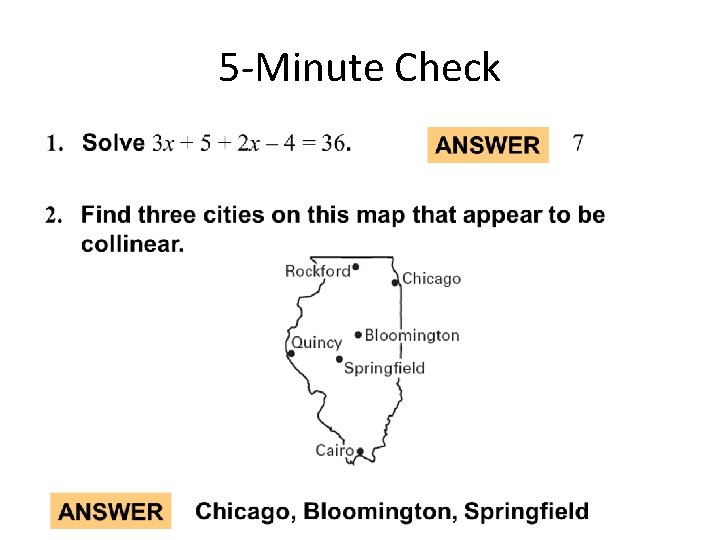
5 Minute Check 1 3 Use Midpoints Distance











- Slides: 17

5 -Minute Check

1. 3 Use Midpoints & Distance Formulas Students will analyze segments and determine lengths in the coordinate plane. Why? So you can solve real world problems dealing with length, as seen in Ex 1. Mastery is 80% or better on 5 -min checks and indy practice.

VOCABULARY • Midpoint: • The point that divides a segment into two congruent segments • Segment bisector: • A point, ray, line segment, or plane that intersects the segment at its midpoint

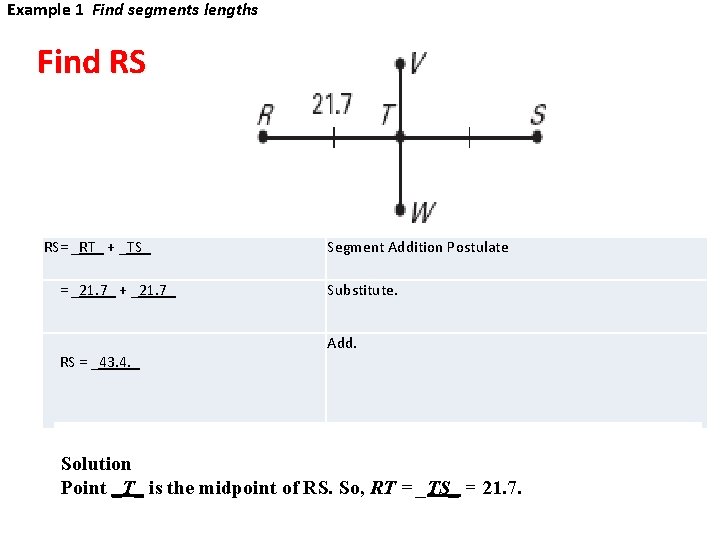
Example 1 Find segments lengths Find RS RS= _RT_ + _TS_ = _21. 7_ + _21. 7_ RS = _43. 4. _ Segment Addition Postulate Substitute. Add. Solution Point _T_ is the midpoint of RS. So, RT = _TS_ = 21. 7.

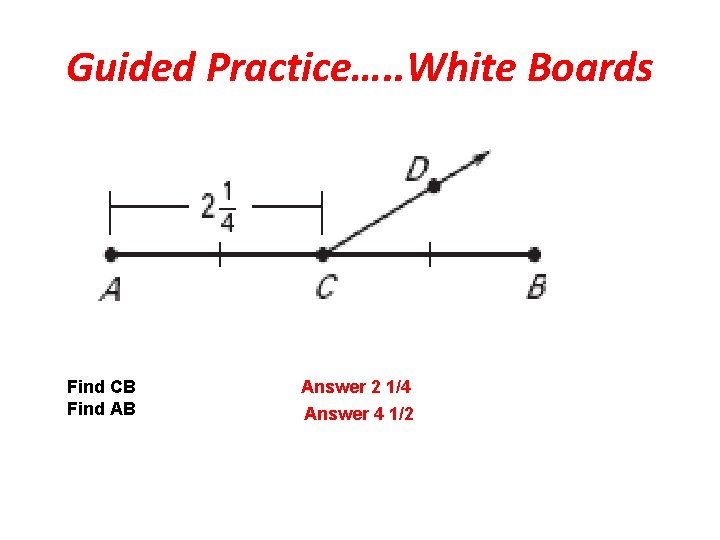
Guided Practice…. . White Boards Find CB Find AB Answer 2 1/4 Answer 4 1/2

Quick Write If B is between AC and collinear is it a midpoint? Explain

Example 2 Use algebra with segment lengths Write and solve an equation. BC = CD _3 x – 2_ = _2 x + 3_ _x – 2_ = _3_ x = _5_ Write equation. Substitute. Subtract _2 x_ from each side. Add _2_ to each side. Step 2 Evaluate the expression for BC when x = _5_ BC = _3 x – 2_ = _3(5) – 2_ = _13_ So, the length of BC is _13_.

Think…. Ink…. . Share Point K is the midpoint of JL. Find the length of JL 8 -3 x=2 x+5 8=5 x+5 3=5 x X=3/5……plug in to solve JL = 12 2/5

5 -Min Check • 1. What does it mean to bisect a segment? • Simply put, it cuts a segment in half. • 2. Line l bisects segment AC at point B. If segment AC is 19 cm, what is the measure of BC? • 9. 5 cm • 3. M is the Midpoint of AC. If AM is x+5 and MC is 2 x, what is the length of AM? • 10

THE MIDPOINT FORMULA • The coordinates of the midpoint of a segment are the averages of the x-coordinates and of the ycoordinates of the endpoints. • If A(x 1, y 1)and B(x 2, y 2) are points in a coordinate plane, then the midpoint M of AB has coordinates

Guided …Example 3 • Use the Midpoint Formula X 1 2 X 2 Y 1 Y 2 2 • The end points of PR are P(– 2, 5) and R(4, 3). Find the coordinates of the midpoint M. • The midpoint of AC is M(3, 4). One endpoint is A(l, 6). Find the coordinates of endpoint C.

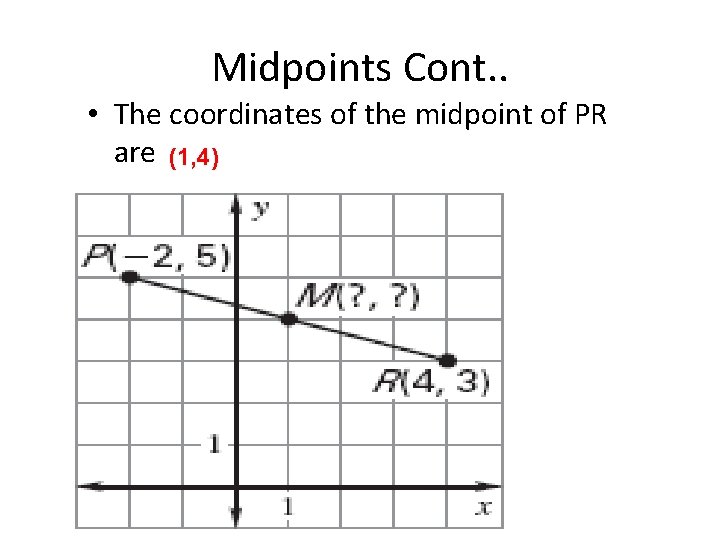
Midpoints Cont. . • The coordinates of the midpoint of PR are (1, 4)

Guided…. Endpoint Option 1 & 2 The midpoint of XZ is M(5, – 6). One endpoint is X(– 3, 7). Find the coordinates of endpoint Z Step 1 Find x. M = (X 1 +X 2) Substitute for what we know. 2 Step 2 Find y. M = (Y 1 + Y 2) Substitute for what we know. 2

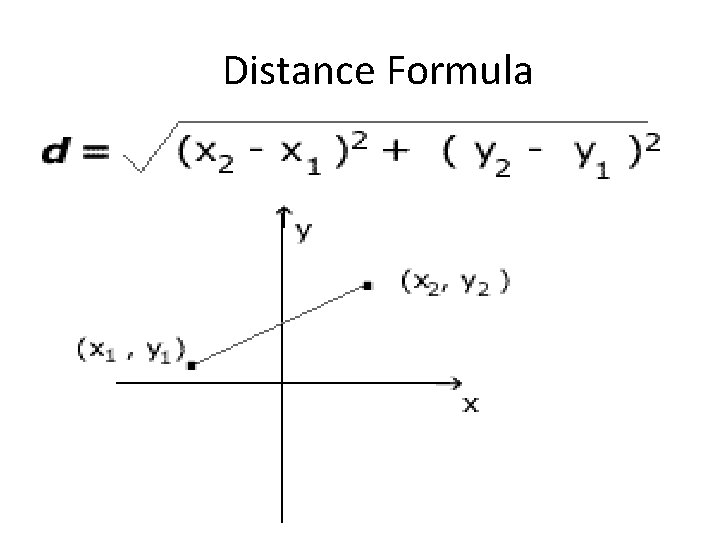
Distance Formula

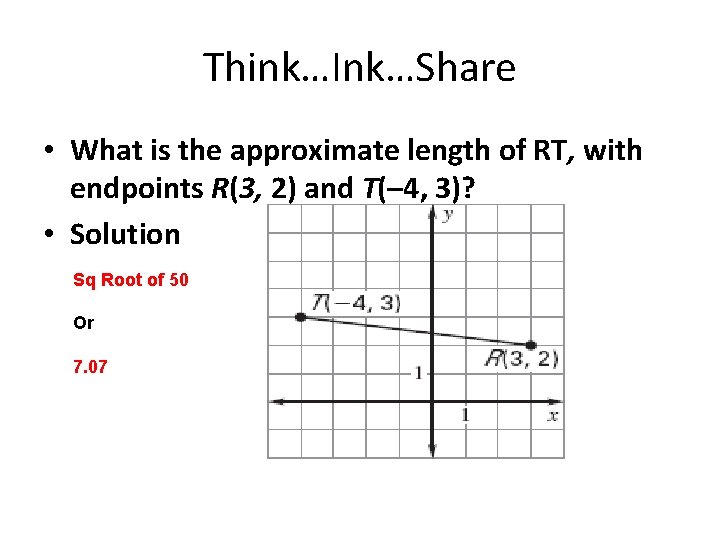
Think…Ink…Share • What is the approximate length of RT, with endpoints R(3, 2) and T(– 4, 3)? • Solution Sq Root of 50 Or 7. 07

What was the Objective for today? • Students will analyze segments and determine lengths in the coordinate plane. • Why? So you can solve real world problems dealing with length, as seen in Ex 1. • Mastery is 80% or better on 5 -min checks and indy practice.

Assignment • PDF Online