5 lecture Questions associated with earlier lecture Programme

5. lecture Questions associated with earlier lecture? Programme: • Group work/term paper • Let’s add measures (2 -> 6 measures) to cost-minization problem developed last time (Vantaanjoki-case) • Let’s add damage function to the problem formulation & solve socially optimal level of nutrient abatement

Term paper You obtain 40 points maximum from the term paper. The idea is to expand or/and combine the weakly exercises. Write the term paper in the form of a typical research paper: • Describe the problem you are focusing on (introduction) • Formulate the problem in a mathematical form (an optimization or estimation problem) (model description)) • Write the matlab code (methods) • Report and interpret the results (Results and Discussion) You may write in English or in Finnish (but not a mixture of the two languages). You may work individually or in pairs. If you choose to work in pairs, please report the contribution of each person. If you have any questions during the process, please contact the person responsible for the lecture you are focusing on. Help can be provided in any phase of the process. Please identify the topics and inform them to Matti (matti. sihvonen@helsinki. fi) before the last lecture Please hand in the term paper by the end of May.

(1) Extensions to Vantaanjoki-model • Let’s add 4 new measures: • two agricultural measures (nutrient management zones ja wetlands) • one measure affecting loading from forests • one measure reflecting additional investment in municipal waste water treatment. • When estimating the effects of agricultural measures (wetlands and management zones), one need to account for the cumulative impacts (i. e. joint impacts of measures on effectiveness)

Kaikkien kuuden muuttujan optimointia varten päivitä: opt_vantaa 1 b. m -> opt_vantaa 2. m clear all global target % target of nutrient abatement global max. Pvah % maximum reductions = capacity global maatkuor; % maatalouden osuus kokonaiskuormituksesta max. Pvah= [13781 10504 3485 6507 811 17016]; maatkuor = 45406; % Measures % (1) fertilization & gypsum % (2) catch crop % (3) zoning % (4) wetland % (5) forestry activities % (6) Investments in wwt X 0 = [0. 1 0. 1]; LB = [0 0 0 0]; UB = [1 1 1 1]; tulokset = []; % alkuarvaus toimenpidevektorille % alarajat toimenpiteille % ylärajat toimenpoiteille for i=1: 10 target = i*2000; [X, FVAL, EXITFLAG] = fmincon(@kustannus 2, X 0, [], [], LB, UB, @rajoitteet 2); tulokset =[tulokset; target X FVAL]; i end

Catch crop Wetland Source: Baltic Deal Zones Fertilization Source: Proagria Source: Hankkija Source: MTK

kustannus 2. m Päivitä kustannus. m - > kustannus 2. m function [totalcosts] = kustannus 2(V) global max. Pvah cost = zeros(1, 6); f={}; f{1}=@(x) f{2}=@(x) f{3}=@(x) f{4}=@(x) f{5}=@(x) f{6}=@(x) 47. 4394 + 62. 8375*exp(0. 000281*x); 29. 479 + 3. 8387*exp(0. 000564*x); 38. 6 + 0. 16*x; 127 + 0. 037*x; 11. 8164 + 0. 0000254*exp(0. 0208*x); 203. 16 + 168. 85*(1 -exp(-0. 00034*x)); % Costs for i=1: length(V) cost(i) = integral(f{i}, 0, V(i)*max. Pvah(i)); end totalcosts = sum(cost); end % % % fertilization & gypsum catch crop zoning wetland forestry activities Investments in wwt

Päivitä rajoitteet. m - > rajoitteet 2. m function [c, ceq] = rajoitteet 2(V) global target global max. Pvah; abat =zeros(1, 6); % toimenpiteiden puhdistukset %Lasketaan toimenpiteiden (1 -2) lannoitus & kipsi ja nurmi & kasvipeitteisyys %vaikutukset muihin toimenpiteisiin (3 -4) suojavyöhykkeet ja kosteikot kerroin =laske. Kertoimet(V, 3, 4); %kerroin-vektori kaikille toimenpiteille 1 -6 % VAIKUTTAVUUS - Vähennys kuormituksesta abat = V. *max. Pvah. *kerroin; c = target-sum(abat); ceq = []; end

laske. Kertoimet. m % Computes the impacts of measures the efficiency of which is altered due to % application of some other measures % eka – first measure affected % vika – last measures affected function [kertoimet] = laske. Kertoimet(V, eka, vika) global max. Pvah; global maatkuor; %By default the multiplier are ones (no effect from other measures) kertoimet = ones(1, length(V)); %Lasketaan kertoimet toimenpiteille ekasta vikaan for i=eka: vika kertoimet(i)=(maatkuor-(V(1: i-1). *kertoimet(1: i-1))*max. Pvah(1: i-1)')/maatkuor; end

y=kerroin

Excercise 5/1. Sensitivity analysis 1. 2. 3. Draw a figure that shows optimal combination of abatement measures as function of target level of nutrient abatement Draw a figure that shows total costs as function of target level of nutrient abatement Compare the results with earlier model runs carried out with only 2 candidate measures. Explain the reasons for differences

(2) Socially optimal level of nutrient abatement • Adjust the minimization problem by adding the health damages from municipal waste water overflows • No given target level (target is the outcome of the optimization) xi D h e ci Measure i application in relation to the maximum level (Amax) Sum of damages and costs damage from eutrophication recreation possibilities & services Health damage from waste water owerflows (bacteria etc) Costs of implmenting the measure

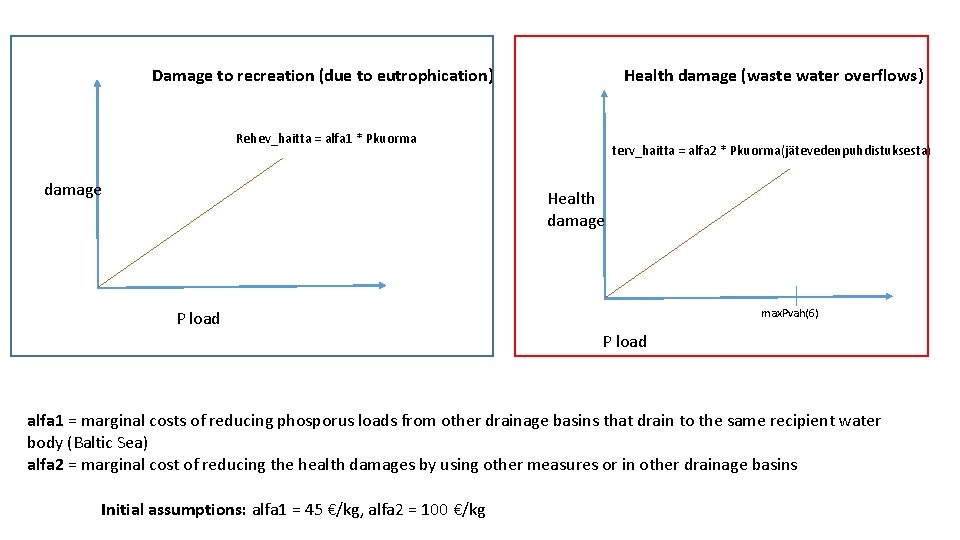
Health damage (waste water overflows) Damage to recreation (due to eutrophication) Rehev_haitta = alfa 1 * Pkuorma damage terv_haitta = alfa 2 * Pkuorma(jätevedenpuhdistuksesta) Health damage max. Pvah(6) P load alfa 1 = marginal costs of reducing phosporus loads from other drainage basins that drain to the same recipient water body (Baltic Sea) alfa 2 = marginal cost of reducing the health damages by using other measures or in other drainage basins Initial assumptions: alfa 1 = 45 €/kg, alfa 2 = 100 €/kg

• New function: vantaa_damage. m • From earlier model versions: • capacity • Cost functions • Effectiveness • New elements: • Health damage • Damage to recreation • Revise optimization accordingly: opt_vantaa 3. m

vantaa_damage. m function [dampluscost] = vantaa_damage(V ) % (1) COSTS OF MEASURES global alfa max. Pvah= [13781 10504 3485 6507 811 17016]; cost = zeros(1, 6); f={}; f{1}=@(x) 47. 4394 + 62. 8375*exp(0. 000281*x); f{2}=@(x) 29. 479 + 3. 8387*exp(0. 000564*x); f{3}=@(x) 38. 6 + 0. 16*x; f{4}=@(x) 127 + 0. 037*x; f{5}=@(x) 11. 8164 + 0. 0000254*exp(0. 0208*x); f{6}=@(x) 203. 16 + 168. 85*(1 -exp(-0. 00034*x)); for i=1: length(V) cost(i) = integral(f{i}, 0, V(i)*max. Pvah(i)); end totalcosts = sum(cost); % % % lannoitus & kipsi nurmi & kasvipeitteisyys suojavyöhykkeet kosteikot metsätoimenpiteet jätevedet % (2) MULTIPLE IMPACTS kertoimet = ones(1, length(V)); eka=3; vika=4; maatkuor=45406; for i=eka: vika kertoimet(i)=(maatkuor-(V(1: i-1). *kertoimet(1: i-1))*max. Pvah(1: i-1)')/maatkuor; end abat = V. *max. Pvah. *kertoimet; % (3) DAMAGES AND COSTS Pkuorma = 80000; % Total P load rehev_haitta = alfa(1)*(Pkuorma-sum(abat)); terveyshaitta = alfa(2)* max. Pvah(6)*(1 -V(6)); dampluscost = rehev_haitta + terveyshaitta + totalcosts ; end

Opt_vantaa 3. m clear all global alfa(1) = 45; alfa(2) = 400; X 0 = [0. 1 0. 1]; toimenpidevektorille LB = [0 0 0 0]; UB = [1 1 1 1]; % alkuarvaus % alarajat toimenpiteille % ylärajat toimenpoiteille tulokset = []; [X, FVAL, EXITFLAG] = fmincon(@vantaa_damage, X 0, [], [], LB, UB)

Excersise 5/2 • Compute the result with default values for alfa 1 (unit damage for recreation) and alfa 2 (healt damage). Does it pay to invest in reducing nutrient loading? (little, much, not at all? ) What measures should be applied? • If alfa 1 is constant (45 €/kg) how large should the marginal health damage (alfa 2) be in order that a) Any investment in measure 6 (investment in waste water treatment) is worthwhile? b) Measures 6 is applied 50% of the capacity? c) Measure 6 is fully adopted with full capacity? • alfa 2=100, how large should the marginal damage to recreation be (alfa 1) so that waste water treatment is fully adopted?

(3) Dynamic model version for optimizing P fertilization Main nutrients: N & P Other nutrients: K, Ca, Se, jne. Management unit: individual field • More or less homogenous piece of land • Parameters described per hectare Kuva: google earth

Optimize P fertilization for a certain piece of agricultural land: Crop yield Initial STP Transition of STP State variable Z x t a T C p Y S r annual profit for a farmer, €/ha Fertilizer input, kg/ha/year 1, …, 100 years price of fertilazer, 4 €/kg Support, 400 €/ha Fixed costs, 423 €/ha crop price, 0. 147 €/kg Yield, kg/ha Soil test phosporus (STP) rate of interest, 0. 03 %

Estimate crop yield function load havainnot. txt a=havainnot (: , 1); % Soil test phosporus b=havainnot (: , 2); % annual crop yield Scatter(a, b) -> curve fitting tool - > Find the best possible functional form and estimate crop yield function

lohkomalli_1. m 1/2 function [Z] = lohkomalli_1(X); % Parameters per = 100; a = 4; T = 400; C = 423; p = 0. 147; r = 0. 03; % % % % Variables Y = zeros(1, per); S = zeros(1, per); profit = zeros(1, per); % crop yield % Soil test phosporus (state variable) % Annual profit, €/ha/yr % Initial state S(1, 1) = 8; % STP initially years price of P fertilizer, €/kg agricultural support, €/ha/yr fixed cost of agriculture, €/ha/yr crop price, €/kg interest rate

lohkomalli_1. m 1/2 % Loop for t=1: per Y(t) = max(0, 0. 6*(-8720 * (S(t))^-0. 67 + 8207)); % crop yield function S(t+1) = 0. 9816*S(t) + (0. 0032+0. 00084*S(t))*(X(t)(3+0. 19*log(S(t))*Y(t)/1000)); end % profit and NPV profit = p*Y - a*X + T - C; Z = - exp(-r*(1: 1: per))* profit'; end % (negative) of the net present value

X=rand(1, 100)*40; % prepare random fertiliation trajectory plot(X) [Z] = lohkomalli_1(X) % run the model % study the development of state variables plot(S) plot(Y) plot(profit)

opt_lohkomalli_1. m 1/1 clear all X 0 = 20*ones(1, 100); % initial guess for P fertilization LB = zeros(1, 100); UB = 300*ones(1, 100); [X, FVAL, EXITFLAG] = fmincon(@lohkomalli_1, X 0, [], [], LB, UB)

Excersise 5/3 (a) Compute optimal trajectory of P fertilization for different initial levels of Soil test phosporus: (S 0=8), (S 0=6), and (S 0=10). Do the trajectories meet, i. e. reach equilibrium in the future? How long does this take? (b) How does the price of fertilizers affect optimal level of fertilization? Compute the results for one initial soil test phosporus level (S 0=8) and three price levels: 3, 4 and 5 euroa/kg