5 KOMPOSISI FUNGSI DAN INVERS FUNGSI Standar Kompetensi






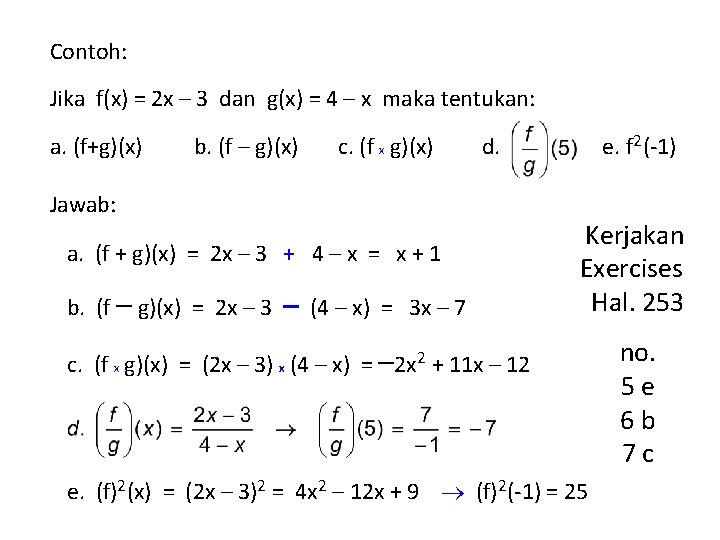



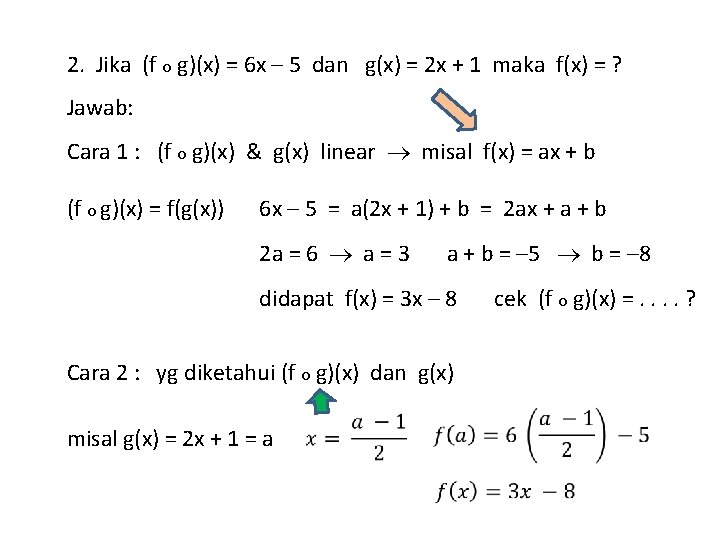

- Slides: 18

5. KOMPOSISI FUNGSI DAN INVERS FUNGSI Standar Kompetensi: 5. Menentukan komposisi dua fungsi dan invers suatu fungsi. Kompetensi Dasar: 5. 1. Menentukan komposisi fungsi dari dua fungsi hal. 240 – 258 Jadwal Ulangan KD 5. 1: 11 IPA 1 : Kamis, 24 Februari 11 IPA 2 : Jumat, 25 Februari 11 IPA 3 : Rabu, 23 Februari

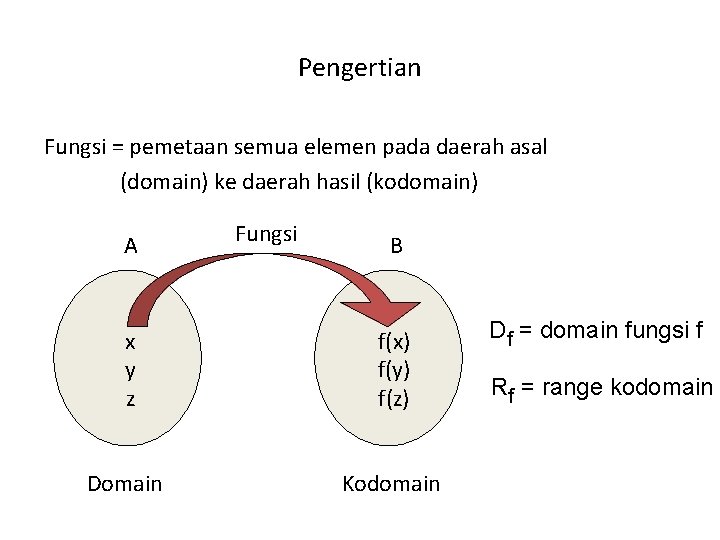
Pengertian Fungsi = pemetaan semua elemen pada daerah asal (domain) ke daerah hasil (kodomain) A Fungsi B x y z f(x) f(y) f(z) Domain Kodomain Df = domain fungsi f Rf = range kodomain

Contoh: Jika f(x) = 2 x + 5 tentukan: a. f(x) untuk domain – 1 ≤ x < 3 , x bil bulat b. Range (Rf) Jawab: Df : – 1, 0, 1, 2 f(– 1) = 2 (– 1) + 5 = 3 f(0) = 5 f(1) = 7 f(2) = 9 Rf : 3 ≤ f(x) ≤ 9

Tambahan Domain Fungsi. . . Khusus untuk fungsi berbentuk akar dan pecahan: Nilai fungsi dalam tanda akar tidak boleh negatif ( f(x) ≥ 0 ) Nilai fungsi penyebut (bawah) tidak boleh NOL Contoh: Tentukan Domain dari: a. f(x) = x 2 + 7 x – 16 Jawab: a. Df : x Real b. x – 3 ≥ 0 Df : x ≥ 3 c. 5 – x ≠ 0 Df : x ≠ 5

SOAL Untuk interval bil. bulat – 3 ≤ x ≤ 5 tentukan Domain (Df) dan Range (Rf) : 1. f(x) = 4 – x 2 2. g(x) = | 2 x + 6 |

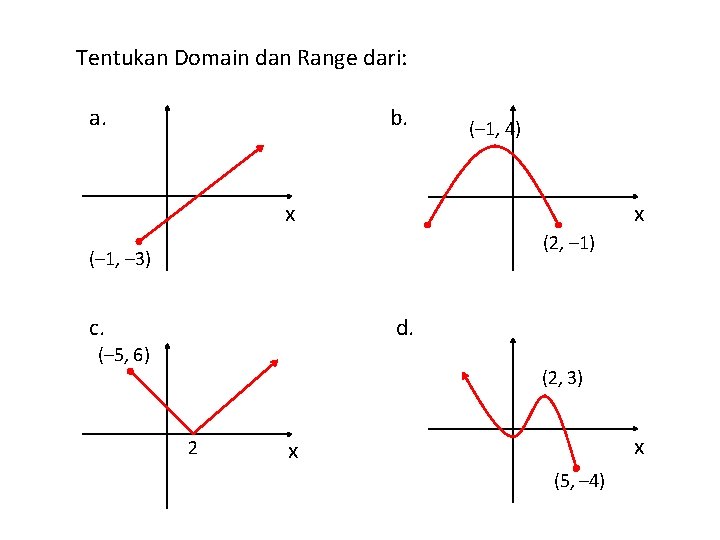
Tentukan Domain dan Range dari: a. b. (– 1, 4) ● x x (2, – 1) (– 1, – 3) d. c. (– 5, 6) (2, 3) ● 2 x x (5, – 4)

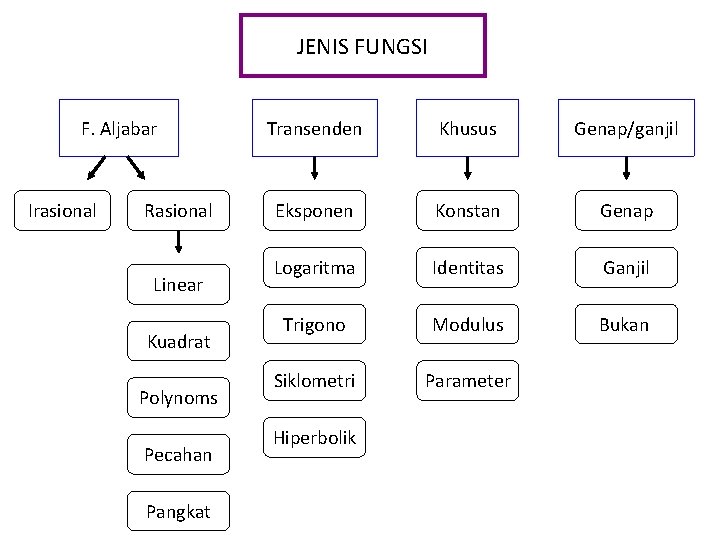
JENIS FUNGSI F. Aljabar Irasional Rasional Linear Kuadrat Polynoms Pecahan Pangkat Transenden Khusus Genap/ganjil Eksponen Konstan Genap Logaritma Identitas Ganjil Trigono Modulus Bukan Siklometri Parameter Hiperbolik

F. Irasional F. Pangkat f(x) = xn F. Eksponen f(x) = 2 x F. Siklometri f(x) = arc sin x F. Hiperbolik f(x) = cosh x F. Konstan f(x) = 3 F. Identitas f(x) = x atau y = x F. Modulus f(x) = | 2 x – 1 | F. Parameter x = at + b , y = t 2 + c F. Genap f(–x) = f(x) F. Ganjil f(–x) = –f(x)

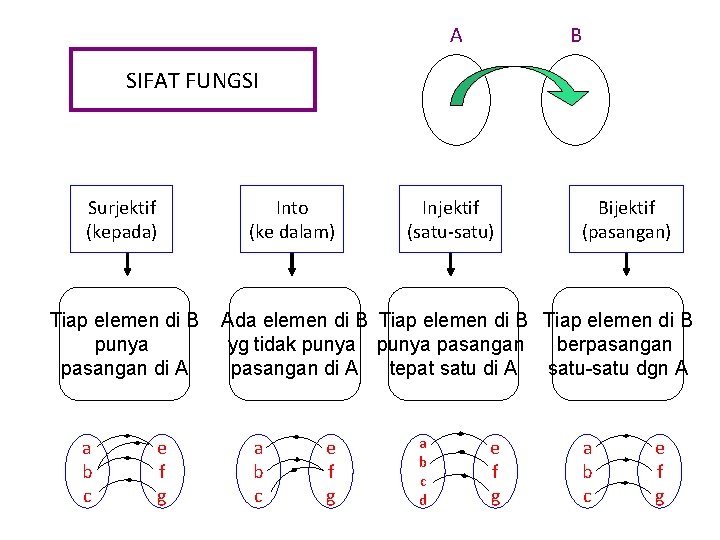
A B SIFAT FUNGSI Surjektif (kepada) Tiap elemen di B punya pasangan di A a b c e f g Into (ke dalam) Injektif (satu-satu) Bijektif (pasangan) Ada elemen di B Tiap elemen di B yg tidak punya pasangan berpasangan di A tepat satu di A satu-satu dgn A a b c e f g a b c d e f g a b c e f g

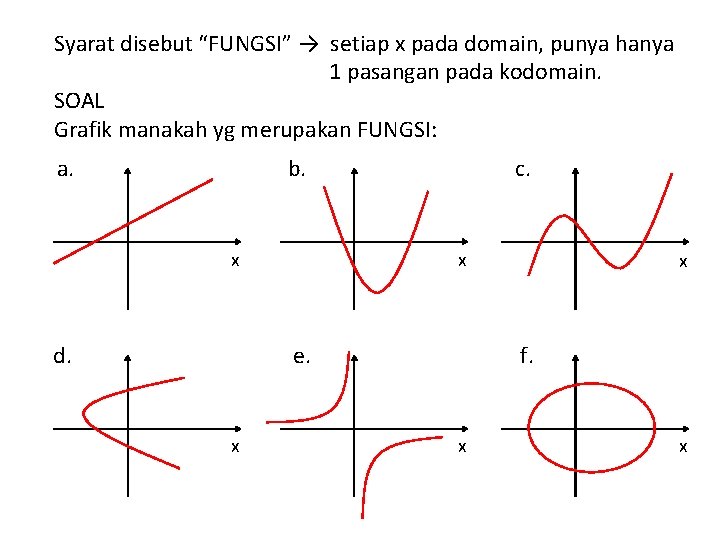
Syarat disebut “FUNGSI” → setiap x pada domain, punya hanya 1 pasangan pada kodomain. SOAL Grafik manakah yg merupakan FUNGSI: a. b. x d. c. x f. e. x x

ALJABAR FUNGSI JIka ada dua fungsi: f(x) dan g(x) , maka berlaku: 1. (f + g)(x) = f(x) + g(x) 2. (f – g)(x) = f(x) – g(x) 3. (f x g)(x) = f(x). g(x) 4. 5. fn(x) = [ f(x) ]n
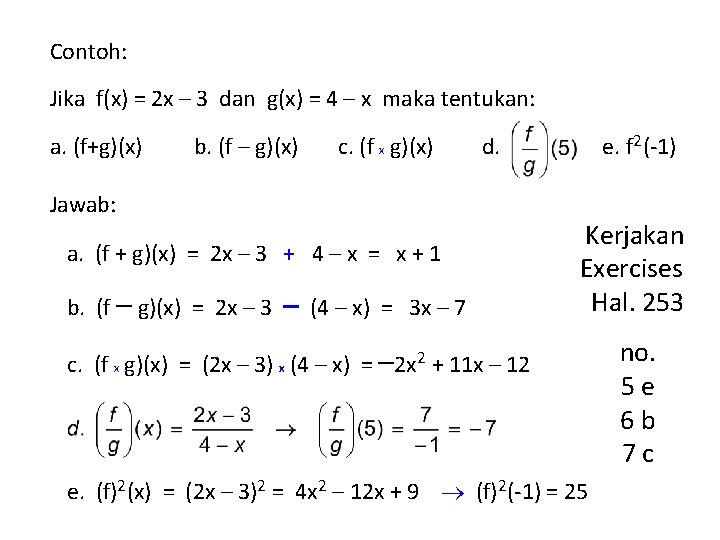
Contoh: Jika f(x) = 2 x – 3 dan g(x) = 4 – x maka tentukan: a. (f+g)(x) b. (f – g)(x) c. (f x g)(x) d. Jawab: a. (f + g)(x) = 2 x – 3 + 4 – x = x + 1 b. (f – g)(x) = 2 x – 3 – (4 – x) = 3 x – 7 e. f 2(-1) Kerjakan Exercises Hal. 253 c. (f x g)(x) = (2 x – 3) x (4 – x) = – 2 x 2 + 11 x – 12 e. (f)2(x) = (2 x – 3)2 = 4 x 2 – 12 x + 9 (f)2(-1) = 25 no. 5 e 6 b 7 c

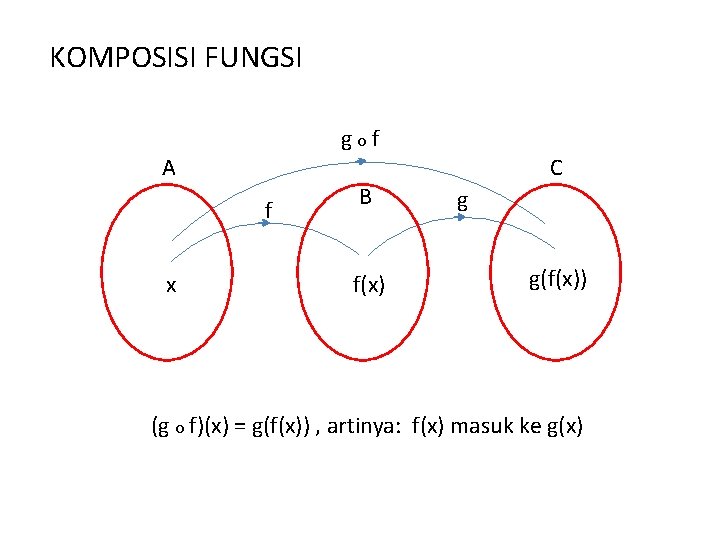
KOMPOSISI FUNGSI g o f A f x B f(x) C g g(f(x)) (g o f)(x) = g(f(x)) , artinya: f(x) masuk ke g(x)

Contoh: Jika f(x) = 2 x – 5 dan g(x) = 3 x + 1 tentukan: a. (f o g)(x) b. (g o f)(x) c. (f o g)(4) Jawab: a. (f o g)(x) = f(g(x)) = 2(3 x + 1) – 5 = 6 x – 3 b. (g o f)(x) = g(f(x)) = 3(2 x – 5) + 1 = 6 x – 14 c. (f o g)(4) = 6. 4 – 3 = 21

SOAL A. Tentukan (f o g)(x) & (g o f)(1) jika: B. Tentukan f(x – 2) jika: 1. f(x) = x 2 – 4 , g(x) = x + 3 1. f(x) = 3 x + 7 2. f(x) = x 2 – x – 6 , g(x) = x 2 + 2 2. f(x) = x 2 + x – 12 C. Tentukan f(x) jika: 1. f(x + 3) = 6 – 5 x 2. f(2 x – 7) = 4 x – 3 3. f(2 – x) = x 2 – 10

Menentukan f(x) atau g(x) jika diketahui komposisinya Contoh: 1. Jika (f o g)(x) = 6 x – 5 dan f(x) = 2 x + 1 maka g(x) = ? Jawab: Cara 1 : (f o g)(x) dan f(x) linear misal g(x) = ax + b (f o g)(x) = f(g(x)) g masuk ke f 6 x – 5 = 2 (ax + b) + 1 = 2 ax + 2 b + 1 2 a = 6 a = 3 2 b + 1 = – 5 b = – 3 didapat g(x) = 3 x – 3 silakan cek (f o g)(x) =. . ? Cara 2 : yg diketahui (f o g)(x) dan f(x) (f o g)(x) = f(g(x)) 6 x – 5 = 2 g + 1 2 g = 6 x – 6 g(x) = 3 x – 3
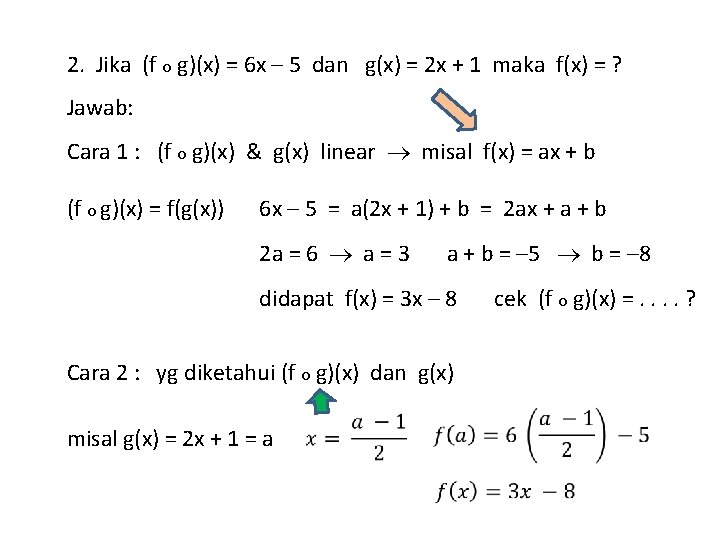
2. Jika (f o g)(x) = 6 x – 5 dan g(x) = 2 x + 1 maka f(x) = ? Jawab: Cara 1 : (f o g)(x) & g(x) linear misal f(x) = ax + b (f o g)(x) = f(g(x)) 6 x – 5 = a(2 x + 1) + b = 2 ax + a + b = – 5 b = – 8 2 a = 6 a = 3 didapat f(x) = 3 x – 8 Cara 2 : yg diketahui (f o g)(x) dan g(x) misal g(x) = 2 x + 1 = a cek (f o g)(x) =. . ?

SOAL 1. Tentukan f(x) jika: 2. Tentukan f(x) jika: a. (f o g)(x) = 4 x + 7 g(x) = 2 x a. (g o f)(x) = 4 x + 7 g(x) = 2 x b. (f o g)(x) = x 2 + 3 x – 6 g(x) = x + 1 b. (g o f)(x) = x 2 + 3 x – 6 g(x) = x + 1 c. (f o g)(x) = x 2 + 3 x – 18 ; c. (g o f)(x) = x 2 + 3 x – 18 ; e. (f o g)(x – 2) = x 2 + x – 12 g(x) = x + 3 e. (g o f)(x – 2) = x 2 + x – 12 g(x) = x + 3 Tambahan: soal dari buku Mandiri, hal. 91 - 97
 Fungsi komposisi dan fungsi invers
Fungsi komposisi dan fungsi invers Rumus fungsi permintaan invers
Rumus fungsi permintaan invers Kompetensi dasar ips
Kompetensi dasar ips Rumus cepat invers
Rumus cepat invers Pengertian grafik fungsi
Pengertian grafik fungsi Misal f(x)=x+1 g(x)=3x dan h(x)=x2
Misal f(x)=x+1 g(x)=3x dan h(x)=x2 Definisi fungsi invers
Definisi fungsi invers Monoton murni
Monoton murni Kompetensi inti dan kompetensi dasar
Kompetensi inti dan kompetensi dasar Hubungan kompetensi inti kompetensi dasar dan indikator
Hubungan kompetensi inti kompetensi dasar dan indikator Pertanyaan tentang kompetensi inti dan kompetensi dasar
Pertanyaan tentang kompetensi inti dan kompetensi dasar Suatu kemampuan untuk
Suatu kemampuan untuk Level kompetensi asn
Level kompetensi asn Standar kompetensi fisioterapi
Standar kompetensi fisioterapi Standar kompetensi pranata laboratorium pendidikan
Standar kompetensi pranata laboratorium pendidikan 9 kompetensi bidan
9 kompetensi bidan Standar kompetensi lulusan kurikulum 2013
Standar kompetensi lulusan kurikulum 2013 Task bidan
Task bidan Contoh iktisar
Contoh iktisar






























