5 Integracin 1 Integrales de lnea de camino

5. Integración 1

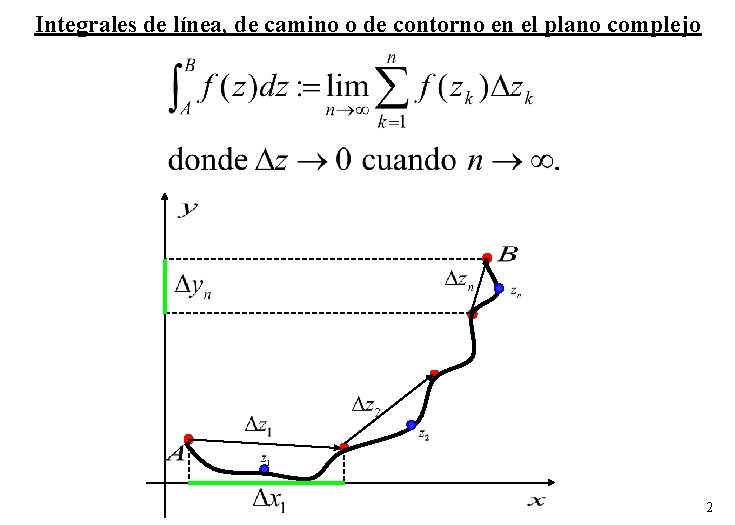
Integrales de línea, de camino o de contorno en el plano complejo 2

Integración de funciones complejas parametrizadas Arco suave C de A a B: Parametrización continua con t(A) t t(B) y con derivadas x’(t) e y’(t) continuas. 3

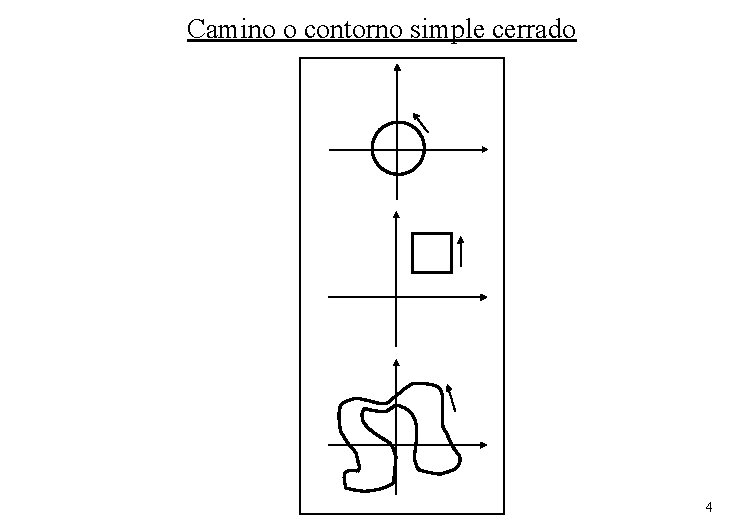
Camino o contorno simple cerrado 4

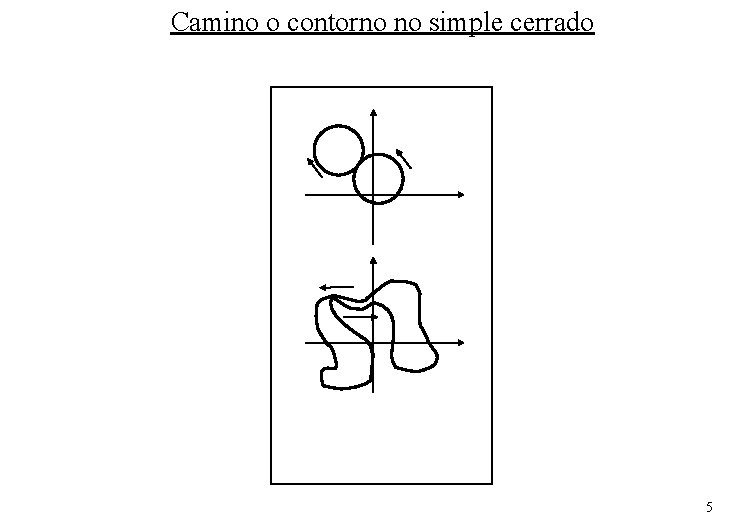
Camino o contorno no simple cerrado 5

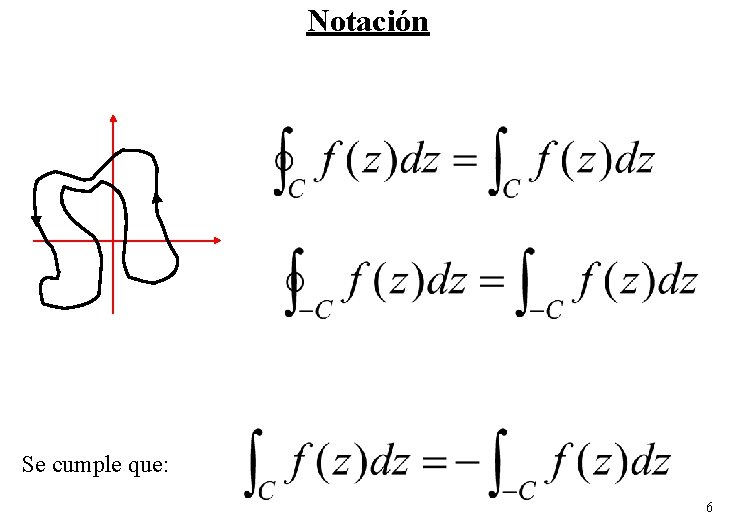
Notación Se cumple que: 6

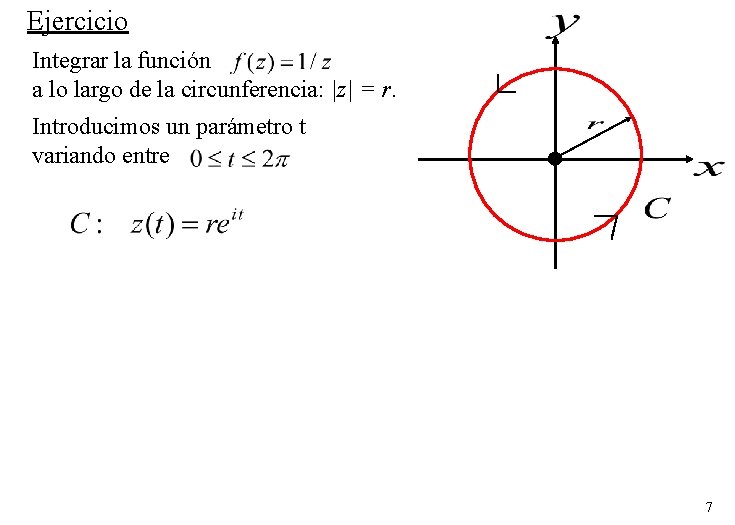
Ejercicio Integrar la función a lo largo de la circunferencia: |z| = r. Introducimos un parámetro t variando entre 7

Teorema integral de Cauchy-Goursat Si f (z) es analítica en todos los puntos dentro y sobre un contorno cerrado C, entonces: 8

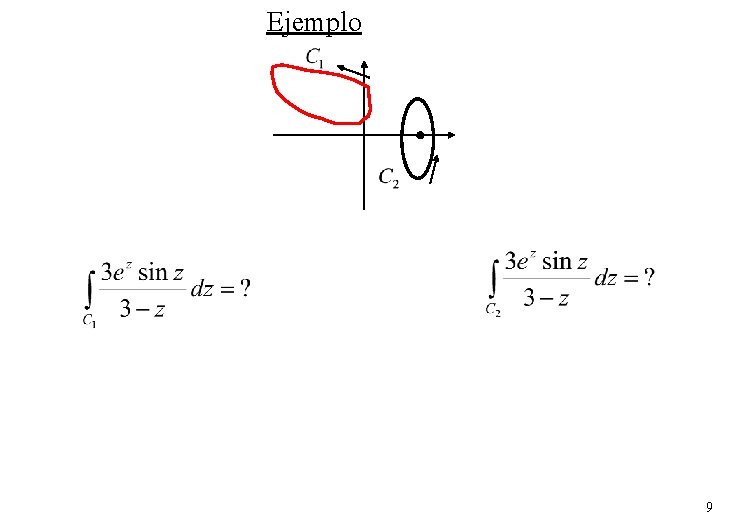
Ejemplo 9

Principio de deformación de contornos (Teorema integral de Cauchy para un dominio doblemente conexo). Supongamos que f (z) es analítica en un dominio doblemente conexo D así como en las curvas que lo limitan. Entonces: 10

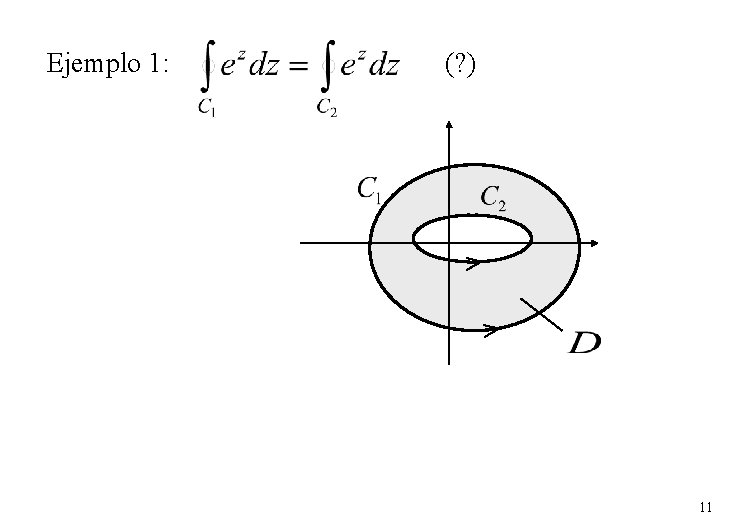
Ejemplo 1: (? ) 11

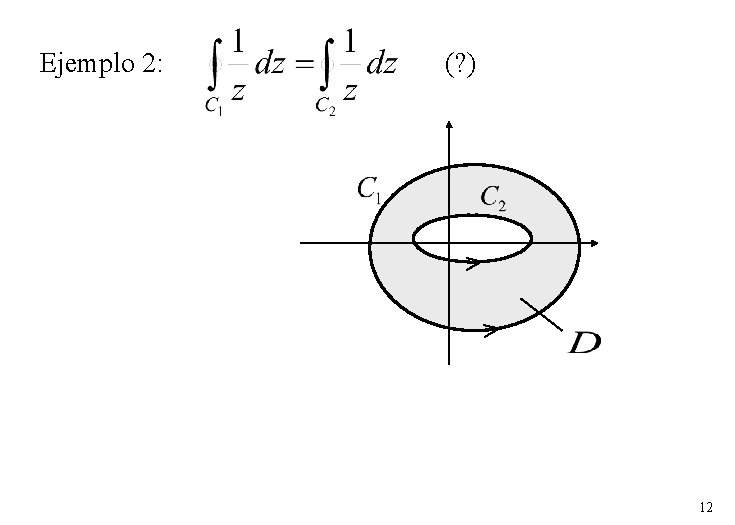
Ejemplo 2: (? ) 12

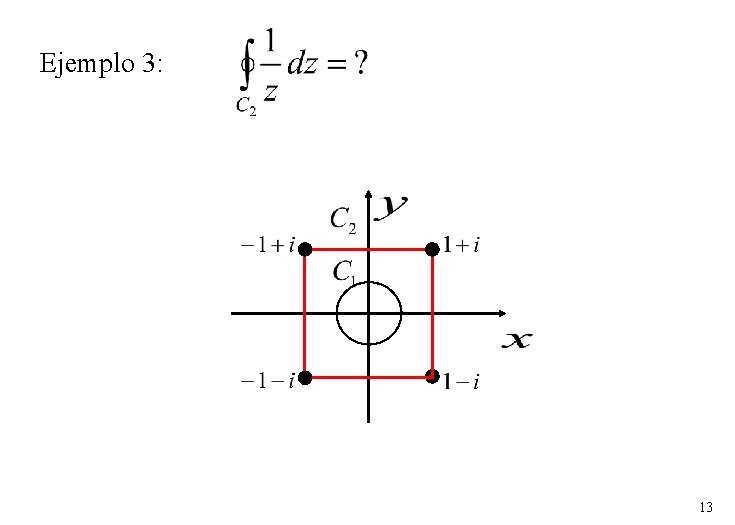
Ejemplo 3: 13

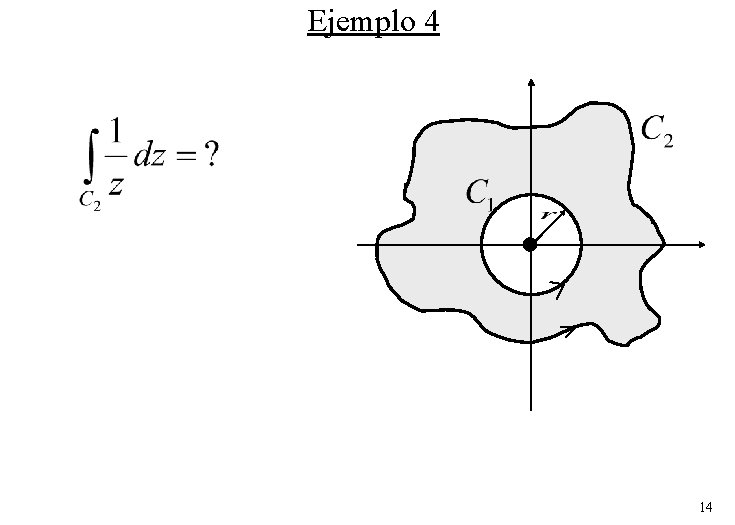
Ejemplo 4 14

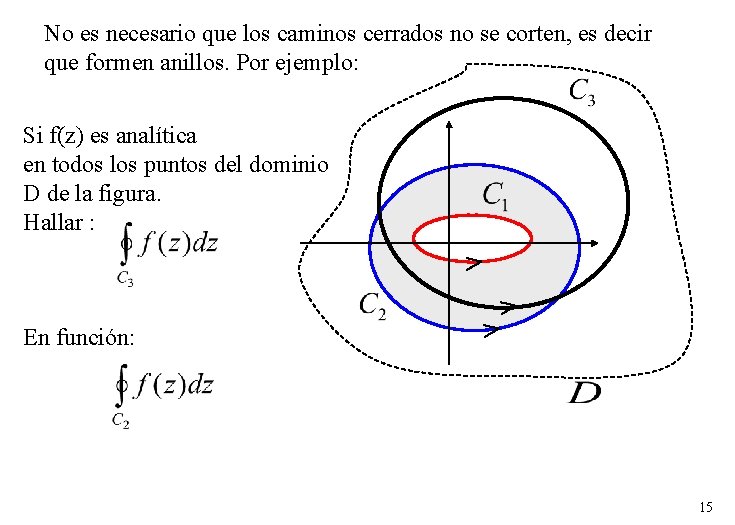
No es necesario que los caminos cerrados no se corten, es decir que formen anillos. Por ejemplo: Si f(z) es analítica en todos los puntos del dominio D de la figura. Hallar : En función: 15

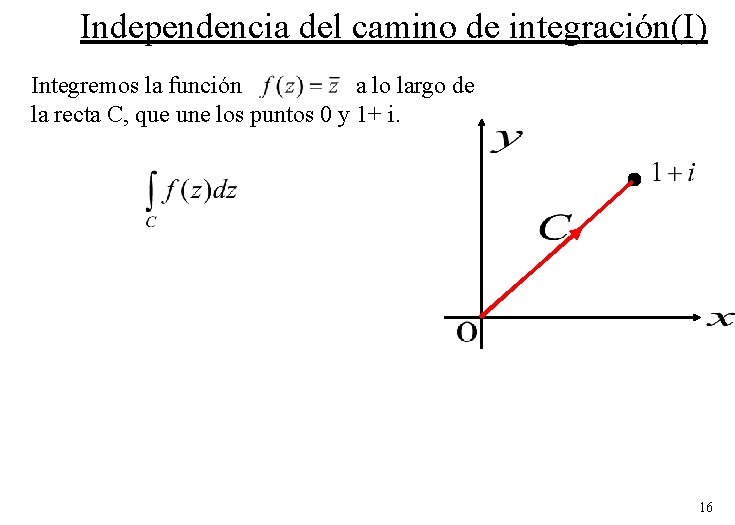
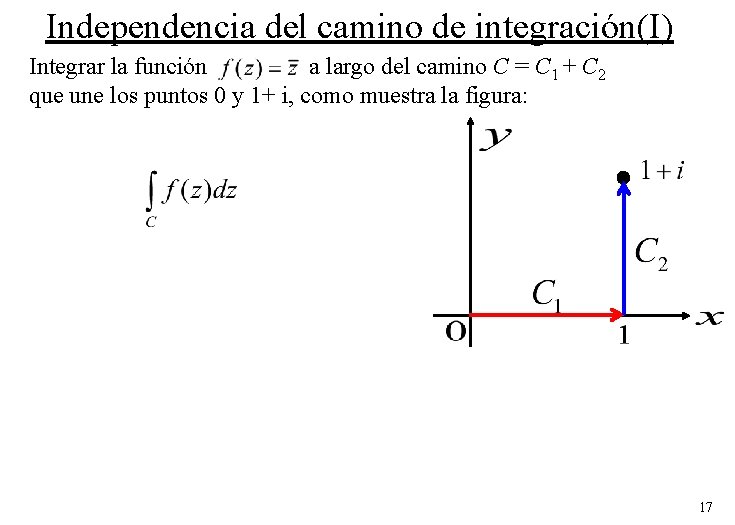
Independencia del camino de integración(I) Integremos la función a lo largo de la recta C, que une los puntos 0 y 1+ i. 16

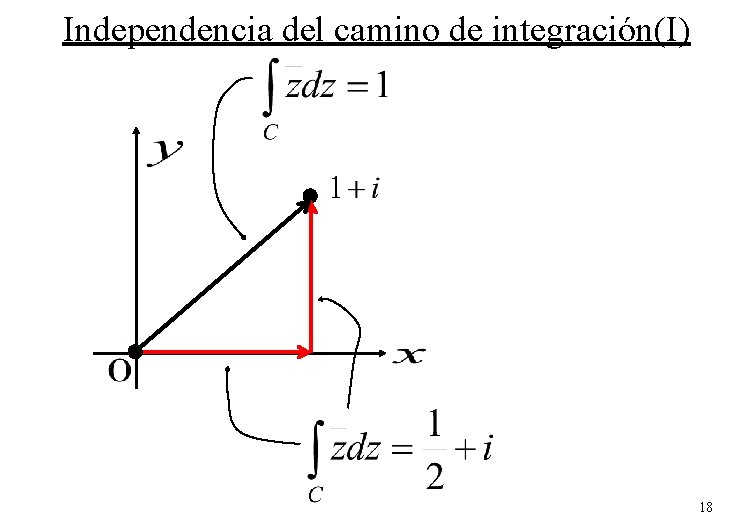
Independencia del camino de integración(I) Integrar la función a largo del camino C = C 1 + C 2 que une los puntos 0 y 1+ i, como muestra la figura: 17

Independencia del camino de integración(I) 18

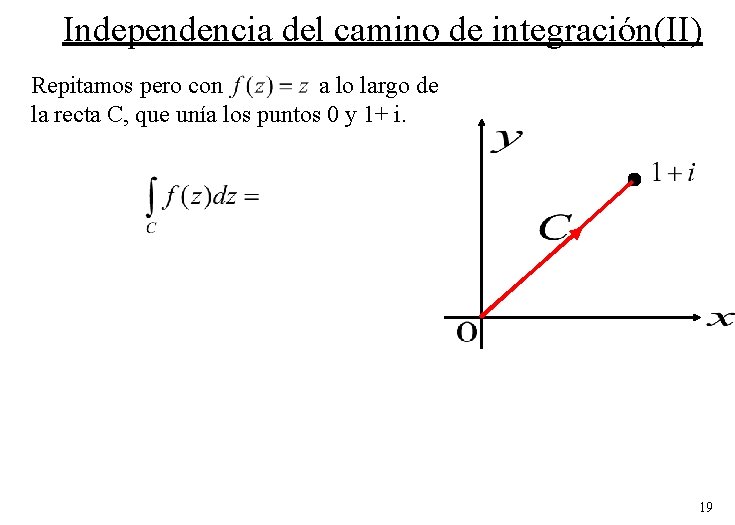
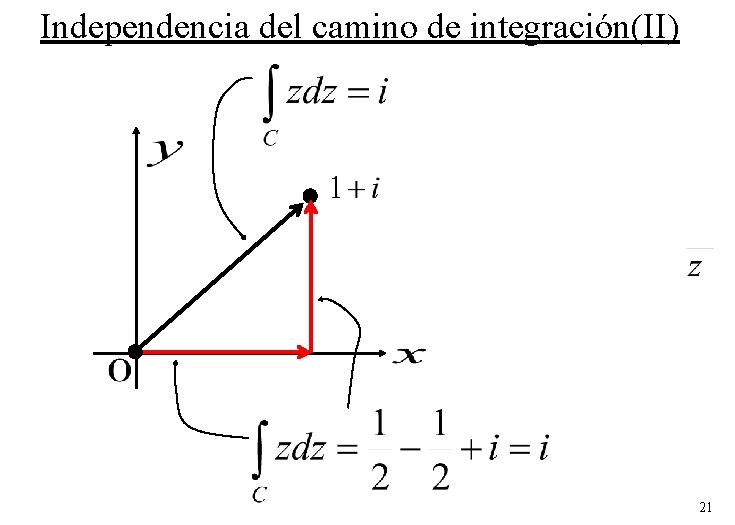
Independencia del camino de integración(II) Repitamos pero con a lo largo de la recta C, que unía los puntos 0 y 1+ i. 19

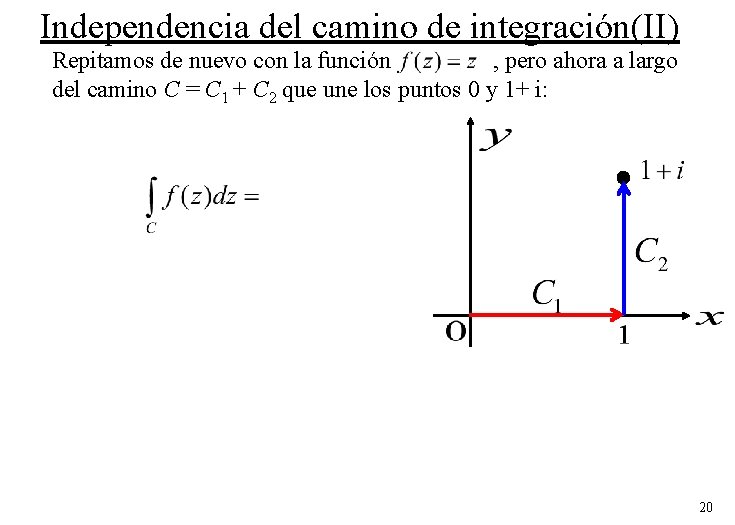
Independencia del camino de integración(II) Repitamos de nuevo con la función , pero ahora a largo del camino C = C 1 + C 2 que une los puntos 0 y 1+ i: 20

Independencia del camino de integración(II) 21

Independencia del camino Supongamos que f (z) es analítica en un dominio simplemente conexo D 22

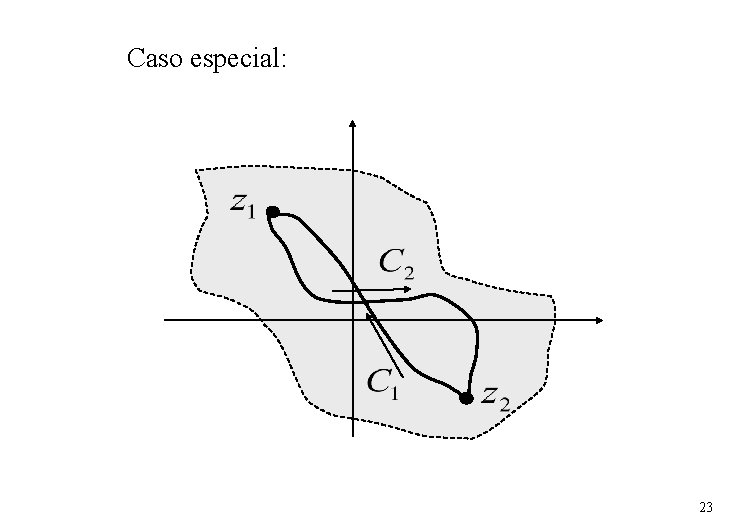
Caso especial: 23

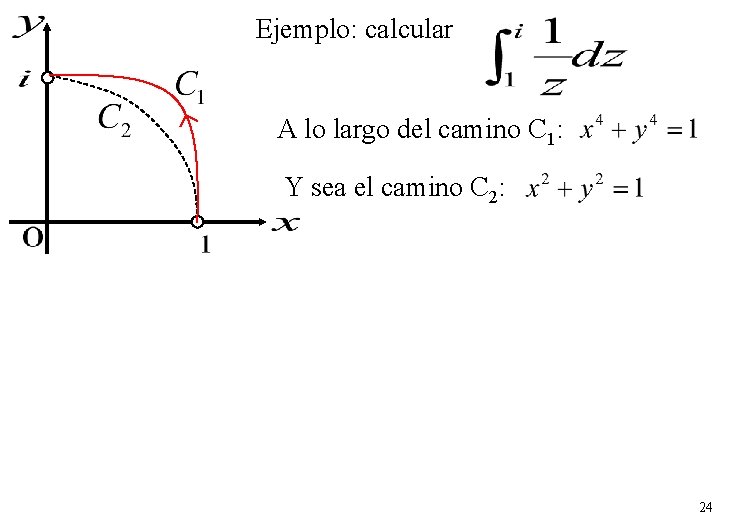
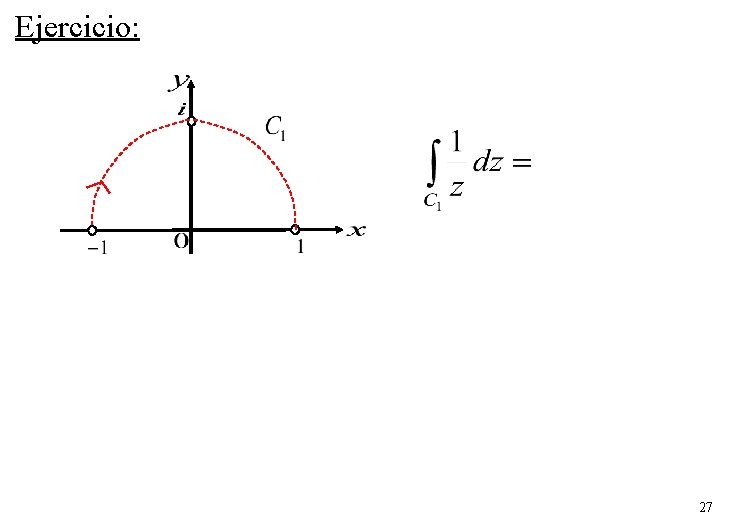
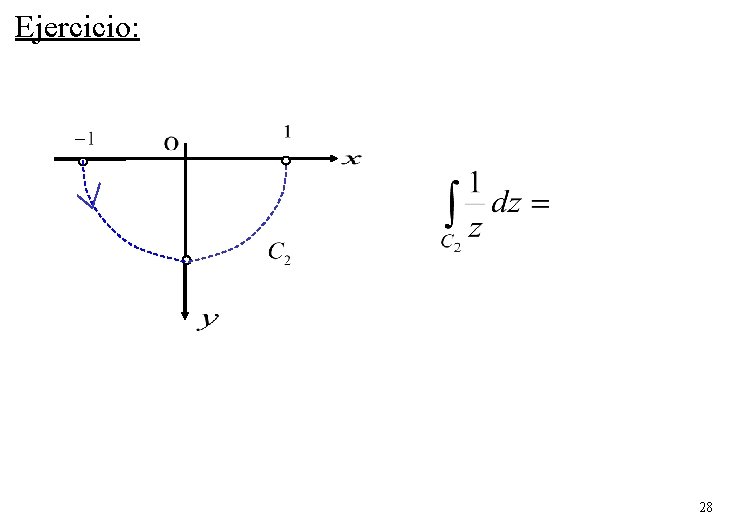
Ejemplo: calcular A lo largo del camino C 1: Y sea el camino C 2: 24

Independencia del camino Consideremos la integral Si F (z) es analítica en un dominio simplemente conexo D con: • d. F/dz = f(z) • z 0 y z 1 están en D Entonces la integral de f(z) entre z 0 y z 1 es independiente del camino en D: 25

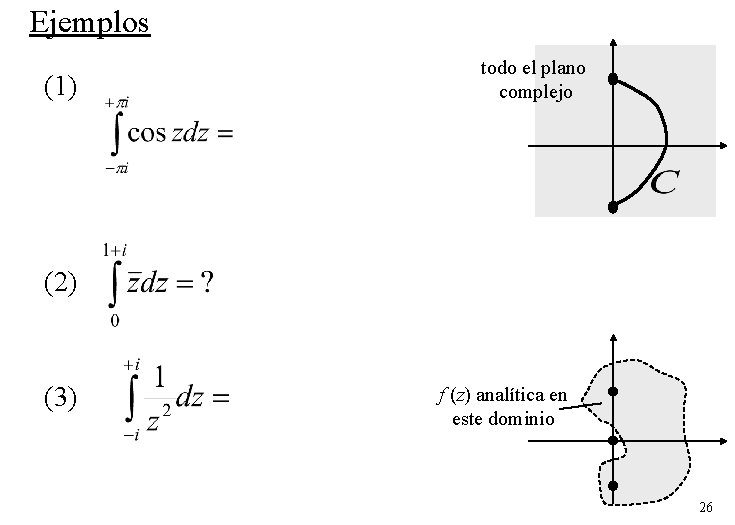
Ejemplos (1) todo el plano complejo (2) (3) f (z) analítica en este dominio 26

Ejercicio: 27

Ejercicio: 28

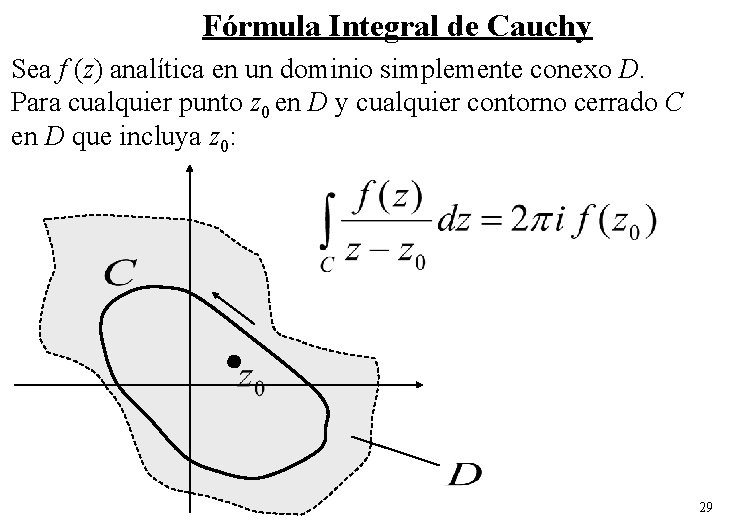
Fórmula Integral de Cauchy Sea f (z) analítica en un dominio simplemente conexo D. Para cualquier punto z 0 en D y cualquier contorno cerrado C en D que incluya z 0: 29

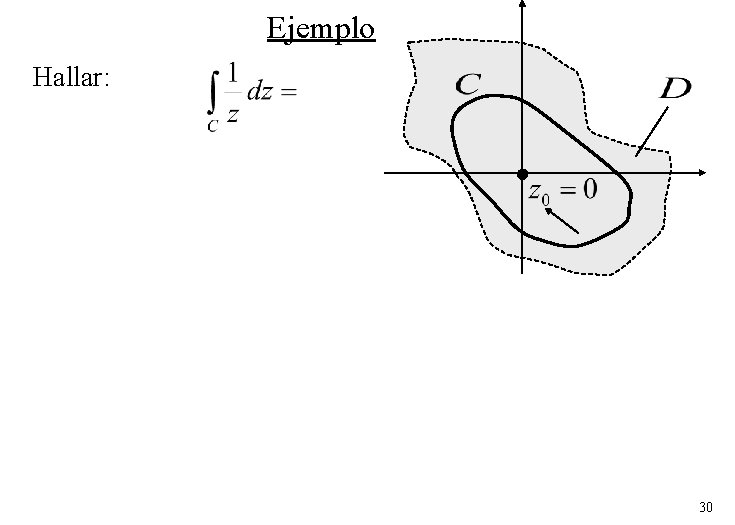
Ejemplo Hallar: 30

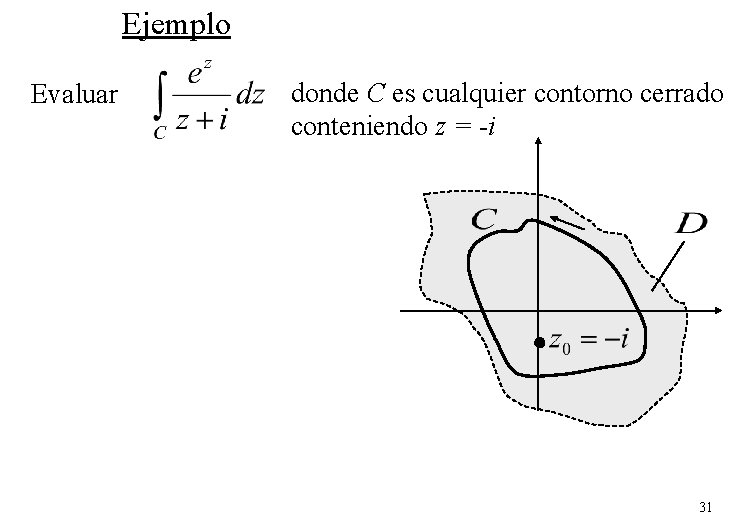
Ejemplo Evaluar donde C es cualquier contorno cerrado conteniendo z = -i 31

Generalización de la fórmula integral de Cauchy Se pueden tratar funciones más complicadas con potencias de z-z 0, con la fórmula: f analítica en y dentro de C, z 0 dentro de C 32

Ejercicio: 33

Conclusiones: Si una función f(z) es analítica en cierto dominio, entonces • Posee derivadas de todos los órdenes en dicho dominio • La derivadas son a su vez también analíticas en el dominio. 34

Resumen: (1) donde F (z) analítica en un dominio simplemente conexo D, con derivada d. F/dz = f(z) y z 0 y z 1 en D. (2) con f (z) analítica dentro y sobre C. ( Teorema integral de Cauchy-Goursat ) 35

Resumen: (3) con f (z) analítica dentro y sobre C (Fórmula integral de Cauchy ) (4) con f (z) analítica dentro y sobre C 36