5 ETUDE GOMTRIQUE 5 1 Introduction Les positions

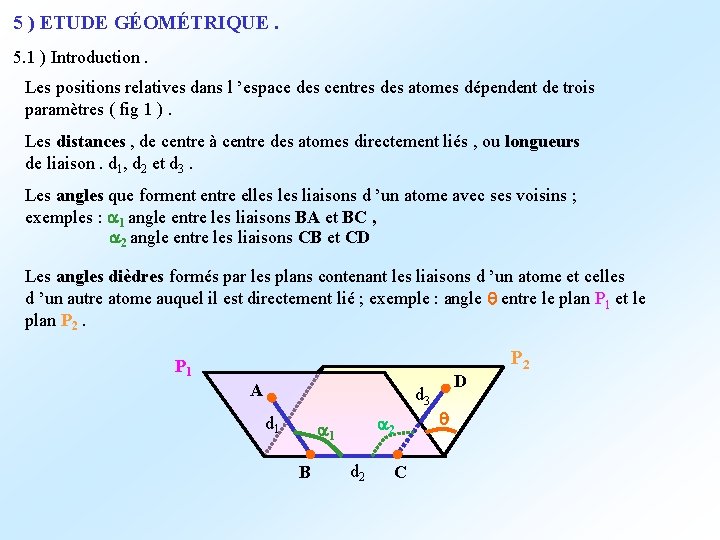
5 ) ETUDE GÉOMÉTRIQUE. 5. 1 ) Introduction. Les positions relatives dans l ’espace des centres des atomes dépendent de trois paramètres ( fig 1 ). Les distances , de centre à centre des atomes directement liés , ou longueurs de liaison. d 1, d 2 et d 3. Les angles que forment entre elles liaisons d ’un atome avec ses voisins ; exemples : a 1 angle entre les liaisons BA et BC , a 2 angle entre les liaisons CB et CD Les angles dièdres formés par les plans contenant les liaisons d ’un atome et celles d ’un autre atome auquel il est directement lié ; exemple : angle entre le plan P 1 et le plan P 2. P 1 A d 3 d 1 a 2 a 1 B d 2 C D P 2

5. 2 ) La longueur des liaisons ( Tableau 1 ).

5. 3 ) L ’orientation des liaisons autour d ’un atome ( exemple ; orientation des liaisons C-H autour de l ’atome de carbone ) peut être prévue en appliquant les règles de Gillespie ou méthode V. S. E. P. R. : Valence Shell Electron Pair Repulsion ou Répulsion des paires électroniques de la couche de valence ). Hypothèse ; soit un atome central , tous les doublets liants et non liants de la couche externe évoluent à la même distance du noyau , comme s ’ils se déplaçaient à la surface d ’une sphère dont le noyau serait le centre. Ces doublets se repoussent mutuellement ; ils se localisent dans des positions qui minimisent ces répulsions électroniques. Par application de ce principe et suivant le nombre de ces doublets , on peut en déduire les directions dans lesquelles se trouvent les doublets liants et donc les liaisons correspondantes.

Méthode ; Déterminer la représentation de LEWIS de l ’espèce considérée ( ne pas oublier les doublets non liants ) . O H NH 3 ; POCl 3 ; Cl P Cl H Cl En déduire la formulation V. S. E. P. R. de l ’espèce de la forme AXn. Ee. A ; atome central ( N pour NH 3 , P pour POCl 3 ) n ; nombres d ’atomes X liés à l ’atome central A : NH 3 ; n = 3 POCl 3 ; n = 4 e ; nombres de doublets non liants ( et électron célibataire ) autour de l ’atome central. NH 3 ; e = 1 POCl 3 ; e = 0 D ’où la formulation V. S. E. P. R. de ces deux espèces. NH 3 ; AX 3 E 1 POCl 3 ; AX 4 E 0

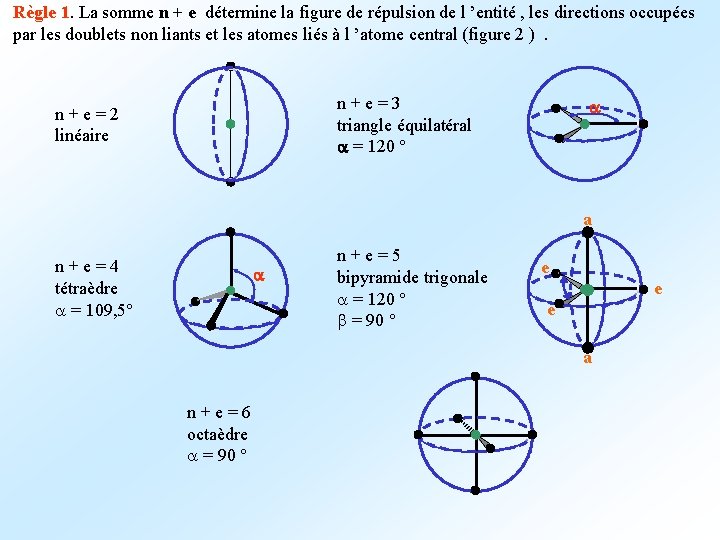
Règle 1. La somme n + e détermine la figure de répulsion de l ’entité , les directions occupées par les doublets non liants et les atomes liés à l ’atome central (figure 2 ) . n + e = 3 triangle équilatéral a = 120 ° n + e = 2 linéaire a a n + e = 4 tétraèdre a = 109, 5° a n + e = 5 bipyramide trigonale a = 120 ° b = 90 ° e e e a n + e = 6 octaèdre a = 90 °

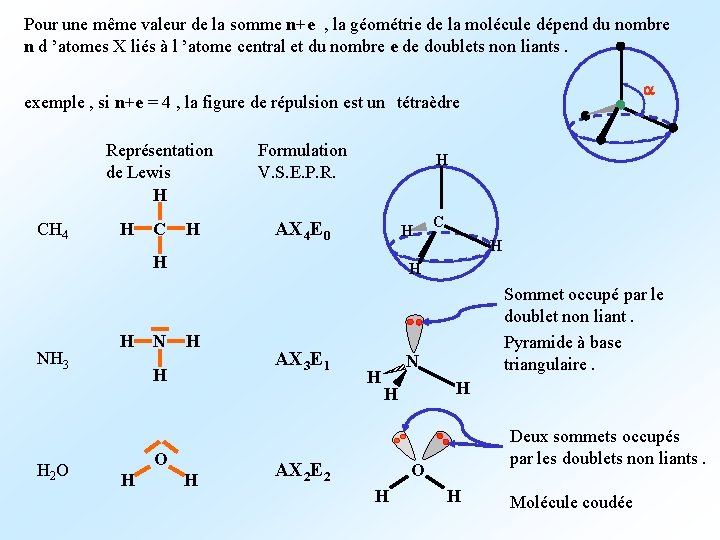
Pour une même valeur de la somme n+e , la géométrie de la molécule dépend du nombre n d ’atomes X liés à l ’atome central et du nombre e de doublets non liants. a exemple , si n+e = 4 , la figure de répulsion est un tétraèdre CH 4 H C H Formulation V. S. E. P. R. H AX 4 E 0 H Représentation de Lewis H H NH 3 H 2 O H N H H O H C H AX 3 E 1 H Sommet occupé par le doublet non liant. Pyramide à base triangulaire. N H H AX 2 E 2 Deux sommets occupés par les doublets non liants. O H H Molécule coudée

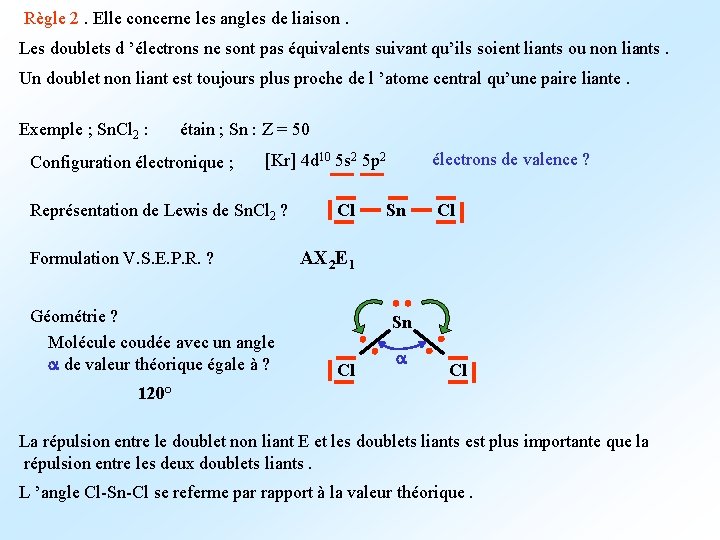
Règle 2. Elle concerne les angles de liaison. Les doublets d ’électrons ne sont pas équivalents suivant qu’ils soient liants ou non liants. Un doublet non liant est toujours plus proche de l ’atome central qu’une paire liante. Exemple ; Sn. Cl 2 : étain ; Sn : Z = 50 Configuration électronique ; électrons de valence ? [Kr] 4 d 10 5 s 2 5 p 2 Représentation de Lewis de Sn. Cl 2 ? Formulation V. S. E. P. R. ? Géométrie ? Molécule coudée avec un angle a de valeur théorique égale à ? Cl Sn Cl AX 2 E 1 Sn Cl a Cl 120° La répulsion entre le doublet non liant E et les doublets liants est plus importante que la répulsion entre les deux doublets liants. L ’angle Cl-Sn-Cl se referme par rapport à la valeur théorique.

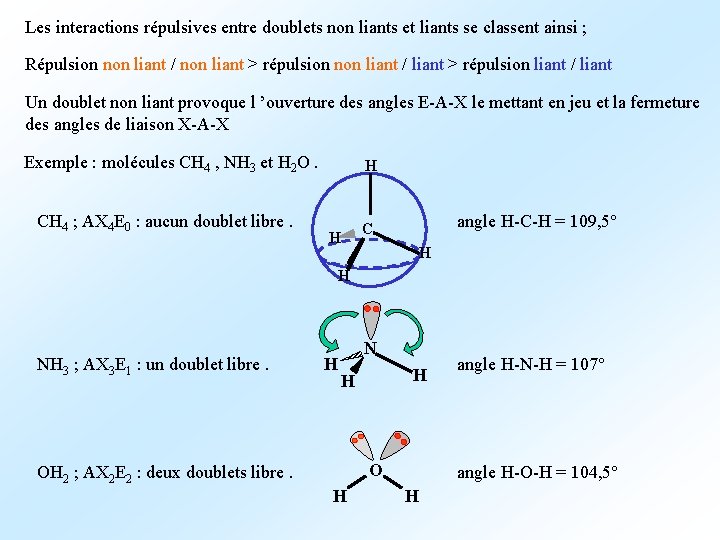
Les interactions répulsives entre doublets non liants et liants se classent ainsi ; Répulsion non liant / non liant > répulsion non liant / liant > répulsion liant / liant Un doublet non liant provoque l ’ouverture des angles E-A-X le mettant en jeu et la fermeture des angles de liaison X-A-X Exemple : molécules CH 4 , NH 3 et H 2 O. H CH 4 ; AX 4 E 0 : aucun doublet libre. H angle H-C-H = 109, 5° C H H NH 3 ; AX 3 E 1 : un doublet libre. H N H H O OH 2 ; AX 2 E 2 : deux doublets libre. H angle H-N-H = 107° angle H-O-H = 104, 5° H

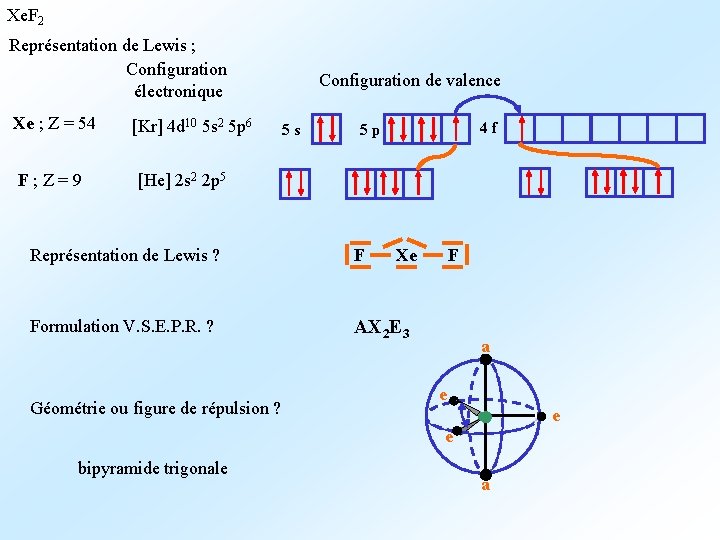
Xe. F 2 Représentation de Lewis ; Configuration électronique Xe ; Z = 54 F ; Z = 9 [Kr] 4 d 10 5 s 2 5 p 6 Configuration de valence 5 s 4 f 5 p [He] 2 s 2 2 p 5 Représentation de Lewis ? F Formulation V. S. E. P. R. ? AX 2 E 3 Géométrie ou figure de répulsion ? Xe F a e e e bipyramide trigonale a

Atomes de fluor en position axiale. F doublets non liants en position e avec des angles de 120° entre les directions qu’ils occupent : 3 répulsions n. L. / n. L. de 120° e e e Les répulsions doublet non liant / doublet non liant sont moins importantes dans cette géométrie : Xe. F 2 est linéaire. F Atomes de fluor en position équatoriale. a e F F 1 doublet non liant en position e et 2 en position a ; angles de 90° entre les directions occupées par les doublets non liants : 2 répulsions n. L. / n. L. de 90° a La géométrie la plus stable est celle qui minimise les répulsions entre doublets non liants

5. 4 ) Polarisation et géométrie . 5. 4. 1 ) Moment dipolaire , ionicité d ’une liaison Lorsque les atomes qui participent à une liaison covalente ont des électronégativités différentes, le doublet électronique mis en commun ne joue plus un rôle symétrique à l ’égard des deux atomes. Il tend à se rapprocher de l ’atome le plus électronégatif. Exemple : H-F Représentation de Lewis ; H F ou H Le fluor est plus électronégatif que l ’hydrogène : F = 4, 0 et H = 2, 2 ( échelle de Pauling : ; khi ). Conséquence ; q. H = + e ; q. F = - e = 0 ; liaison purement covalente = 1 ; liaison purement ionique F + e - e H F P e : charge élémentaire ( 1, 6 10 -19 C) q. H = +e ; q. F = -e La polarisation est caractérisée par le moment dipolaire P

La polarisation est caractérisée par le moment dipolaire P q = e en coulomb C P = q d. AB (d. HF) d en m P en C. m ou debye D + e H P - e F 1 D = 3, 33 10 -30 C. m Ionicité I ou pourcentage ionique Pexp : moment dipolaire expérimental de la liaison A-B Pthéo : moment dipolaire de la liaison supposée être purement ionique ( q = e dans l ’exemple de H-F) Plus la liaison est polaire plus q ( e ) tend vers e Plus Pexp tend vers Pthéo et plus I augmente Application ; H-Cl ; Pexp = 1, 07 D ; d. HCl = 1, 28 10 -10 m Calculer la valeur de q puis l ’ionicité de la liaison H-Cl

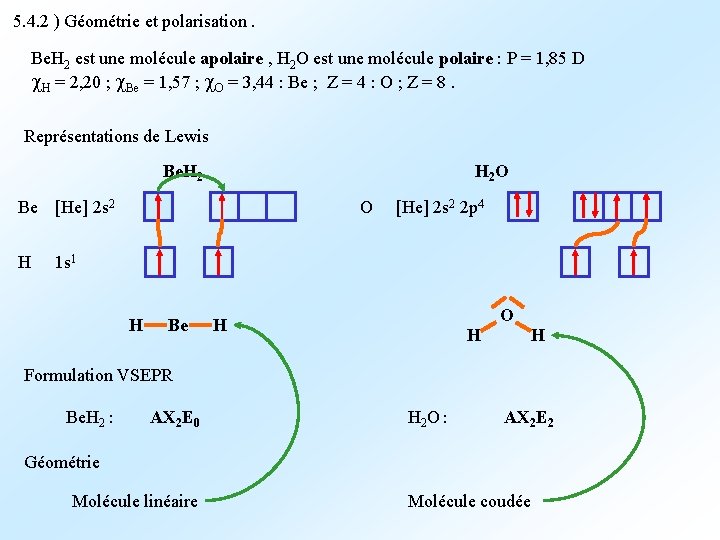
5. 4. 2 ) Géométrie et polarisation. Be. H 2 est une molécule apolaire , H 2 O est une molécule polaire : P = 1, 85 D H = 2, 20 ; Be = 1, 57 ; O = 3, 44 : Be ; Z = 4 : O ; Z = 8. Représentations de Lewis Be. H 2 O Be [He] 2 s 2 H O [He] 2 s 2 2 p 4 1 s 1 H Be O H H H Formulation VSEPR Be. H 2 : AX 2 E 0 H 2 O : AX 2 E 2 Géométrie Molécule linéaire Molécule coudée

Données : H = 2, 20 ; Be = 1, 57 ; O = 3, 44 Polarisation des liaisons Be. H 2 p 1 H - e Be +2 e p 2 H 2 O H - e p 1 H + e O -2 e p 2 H + e p p = p 1 + p 2 = 0 La molécule est apolaire Le moment dipolaire résultant est non nul La molécule est polaire Application ; le dioxyde de carbone CO 2 est une molécule apolaire : le dioxyde de soufre SO 2 est une molécule polaire P = 1, 58 D. Interpréter cette différence. Justifier la valeur de l ’angle O-S-O dans SO 2 119, 5°. Données : C = 2, 55 ; S = 2, 58 6 ) Hybridation