5 Continuity on an Interval Continuity definition revisited

5. Continuity on an Interval

Continuity definition revisited Remember the definition of continuity When asked about continuity, check all 3 things, then make a concluding statement

Example 1 Discuss the continuity of

Example 2 Find the value of a so that the function is continuous at x = -1.

Example 3 Find the value of a and b so that the function is continuous at x = 1.

Continuity on an interval A function f(x) is continuous on an open interval (a, b) if and only if the function f(x) is continuous at every point in the interval (a, b) A function f(x) is continuous on a closed interval [a, b] if and only if it is continuous on open interval (a, b) and if the endpoints exhibit the following: In words, this means there must be a closed dot.

Example 4 Revisiting the graph of f(x), graphus interruptus, determine whether the function is continuous on given intervals. If not, explain. A) (-5, -2) B) (-5, -2] C) [-5, -2) D) [-5, -2] E) [0, 4] F) [6, 8) G) (2, 4) H) Find the largest value of b such that the function is continuous on (5, b] but not on (5, b+1]. i) Give the largest interval for a such that the function is continuous on (a, 10).

Functions that are continuous for all values in their domain Polynomials – all real numbers Rational functions (VAs and holes not in domain) Root functions (where value under square root > 0) Trig functions (sin and cos – all real numbers, others not at VA) Exponential functions – all real numbers Log functions (where value of log > 0)

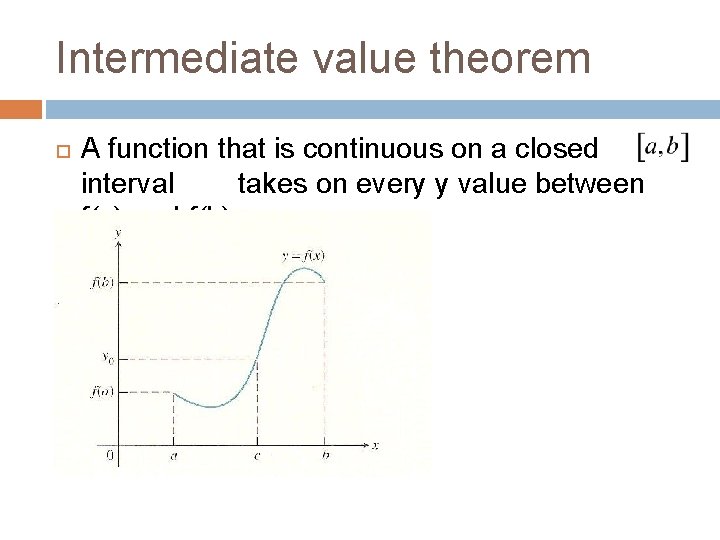
Intermediate value theorem A function that is continuous on a closed interval takes on every y value between f(a) and f(b).

In other words…. . A function that is continuous can’t skip y values Note: Even though the function can’t skip y values, it can take on values that are outside of f(a) and f(b)

Example 5

Existence of zeros The IVT can be used to show the existence of zeros If one value of the function is negative and another is positive, there must be a zero somewhere in between

Example 6

Example 7 Here’s part of an example from the Free Response section of the 2007 AP exam. The functions f and g are differentiable (and continuous) for all real numbers, and g is strictly increasing. The function h is given by h(r)=f(g(r)) -6. Explain why there must be a value r for 1<r<3 such that h(r) = -5.