5 Compound nucleus reactions Prof Dr A J

5. Compound nucleus reactions Prof. Dr. A. J. (Arjan) Koning 1, 2 1 International 2 Division Atomic Energy Agency, Vienna of Applied Nuclear Physics, Department of Physics and Astronomy, Uppsala University, Uppsala, Sweden Email: A. koning@iaea. org EXTEND European School on Experiment, Theory and Evaluation of Nuclear Data, Uppsala University, Sweden, August 29 - September 2, 2016

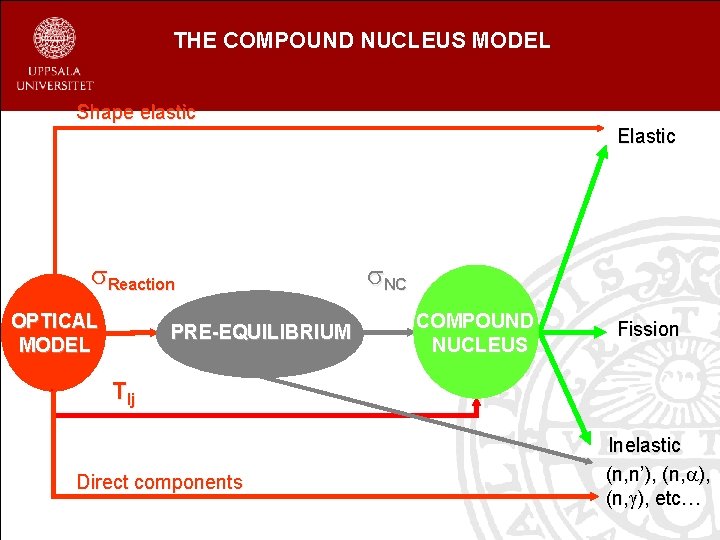
THE COMPOUND NUCLEUS MODEL Shape elastic Elastic Reaction OPTICAL MODEL PRE-EQUILIBRIUM NC COMPOUND NUCLEUS Fission Tlj Direct components Inelastic (n, n’), (n, ), etc…

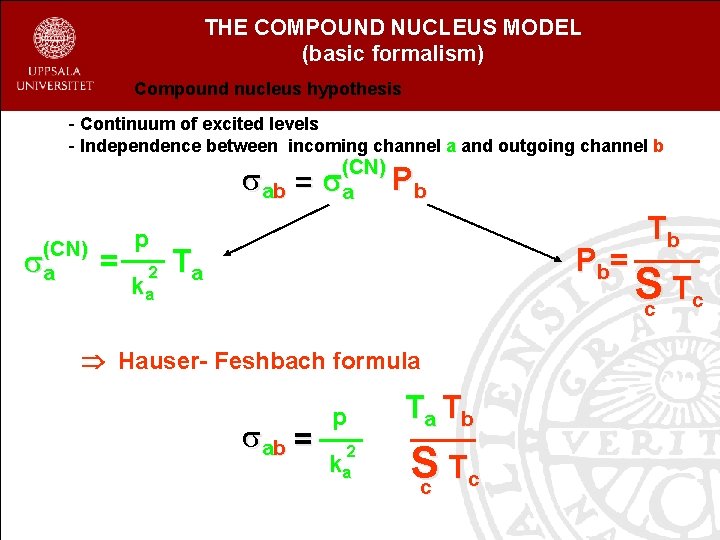
THE COMPOUND NUCLEUS MODEL (basic formalism) Compound nucleus hypothesis - Continuum of excited levels - Independence between incoming channel a and outgoing channel b a b = (CN) a = p 2 ka (CN) a Pb P b= Ta Hauser- Feshbach formula a b = Ta Tb p 2 ka Sc Tc Tb Sc Tc

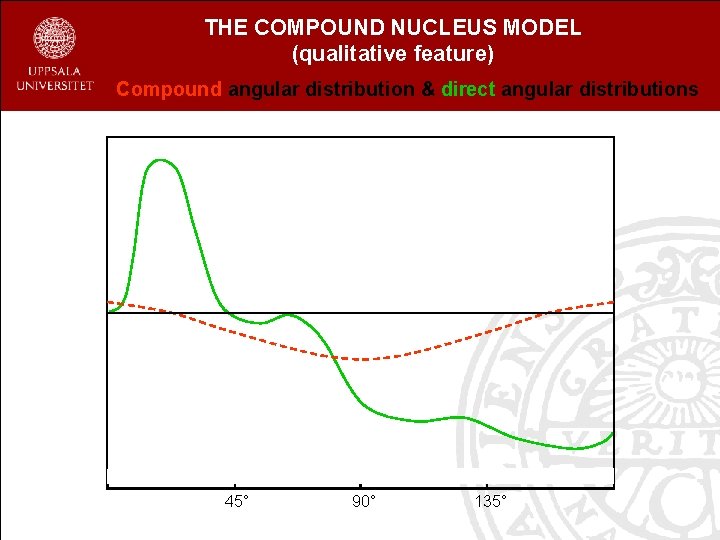
THE COMPOUND NUCLEUS MODEL (qualitative feature) Compound angular distribution & direct angular distributions 45° 90° 135°

THE COMPOUND NUCLEUS MODEL (complete channel definition) Channel Definition a + A (CN )* b+B Incident channel a = (la, ja=la+sa, JA, p. A, E A, E a) Conservation equations • Total energy : Ea + EA = ECN = Eb + EB • Total momentum : pa + p. A = p. CN = pb + p. B • Total angular momentum : la + sa + JA = JCN = lb + sb + JB • Total parity : p. A (-1)la = p. CN = p. B (-1)lb

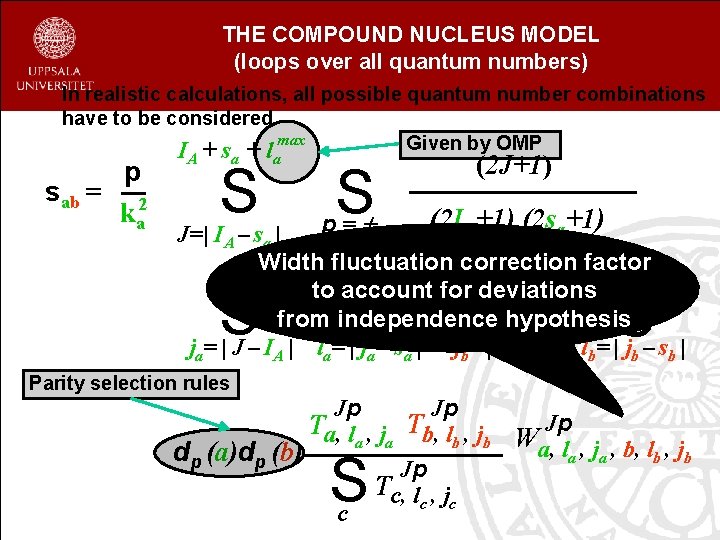
THE COMPOUND NUCLEUS MODEL (loops over all quantum numbers) In realistic calculations, all possible quantum number combinations have to be considered max Given by OMP I +s +l p sab = 2 ka A a S p= (2 J+1) (2 IA+1) (2 sa+1) J=| IA – sa | Width fluctuation correction factor J + IA j a + sa + IB j b + sb to account for Jdeviations from independence hypothesis ja= | J – IA | la= | ja – sa | jb= | J – IB | lb= | jb – sb | S S Parity selection rules T Jp Ta, l , j Tb, l , j W b b a a a, la , ja , b, lb , jb dp (a)dp (b) T Jp Tc, l , j c c c S

THE COMPOUND NUCLEUS MODEL (the GOE triple integral)

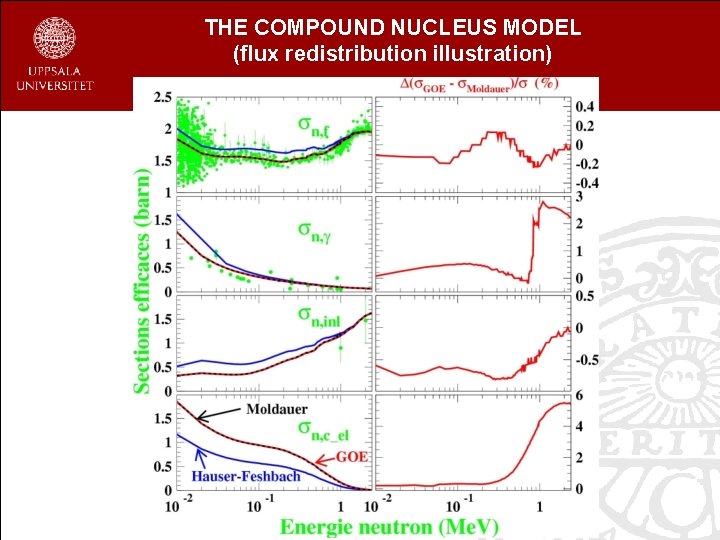
THE COMPOUND NUCLEUS MODEL (flux redistribution illustration)

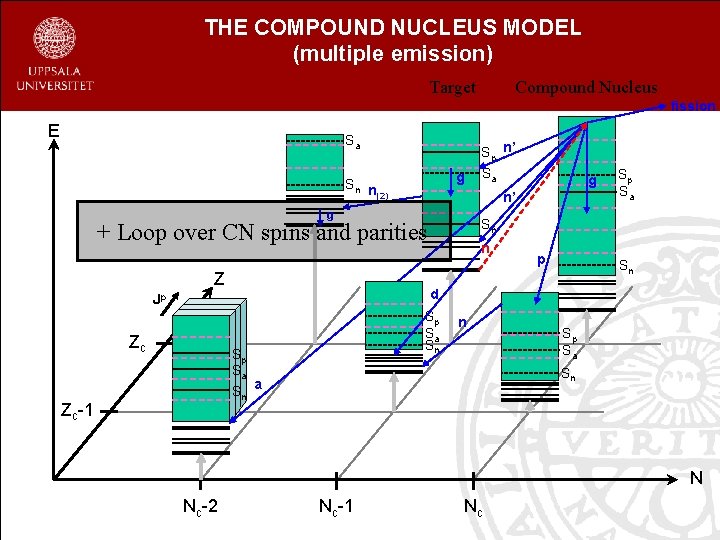
THE COMPOUND NUCLEUS MODEL (multiple emission) Target Compound Nucleus fission E Sa g Sn n (2) n p Sn d Jp Sp Sa Sn Sn a Zc-1 Sp Sa Sn + Loop over CN spins and parities Zc g n’ g Z Sp n’ Sa N Nc-2 Nc-1 Nc

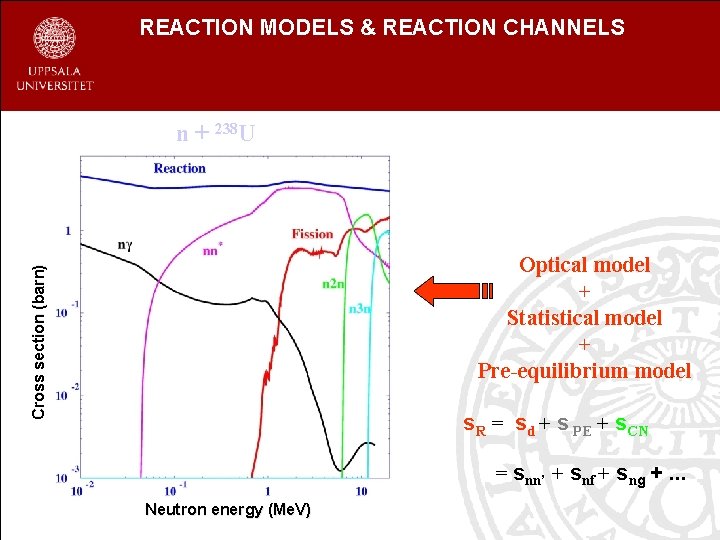
REACTION MODELS & REACTION CHANNELS n + 238 U Cross section (barn) Optical model + Statistical model + Pre-equilibrium model s. R = sd + s PE + s. CN = snn’ + snf + sng +. . . Neutron energy (Me. V)

THE COMPOUND NUCLEUS MODEL (compact expression) NC = ab where b = g , n, p, d, t, …, fission b ab = 2 k a J, a, b 2 J+1 2 s+1 2 I+1 < > J Tb b J Tlj a J d with J = la + sa + IA = ja + IA and = -1 and < > Tb(b) la Wab Td d A = transmission coefficient for outgoing channel b associated with the outgoing particle b

THE COMPOUND NUCLEUS MODEL (various decay channels) Possible decays • Emission to a discrete level with energy Ed < > Tb(b) Jp = Tlj(b) given by the O. M. P. • Emission in the level continuum < > Tb(b) = E +DE Jp Tlj(b) r(E, J, p) d. E E r(E, J, p) density of residual nucleus’ levels (J, p) with excitation energy E • Emission of photons, fission Specific treatment

Exercise • Neutrons + Cu-65 • Two incident energies: 1. 6 and 5. 5 Me. V • Plot elastic scattering angular distributions for both of them: the direct, compound and total component • Exp data: 1. 6 Me. V: Cu-0, 5. 5 Me. V: Cu-65 • Use TALYS sample case 3 for inspiration 13