5 8 Susunan bilangan atau bilangan yang disusun

5 8 Susunan bilangan atau bilangan yang disusun ke dalam bentuk baris atau bentuk lajur 2

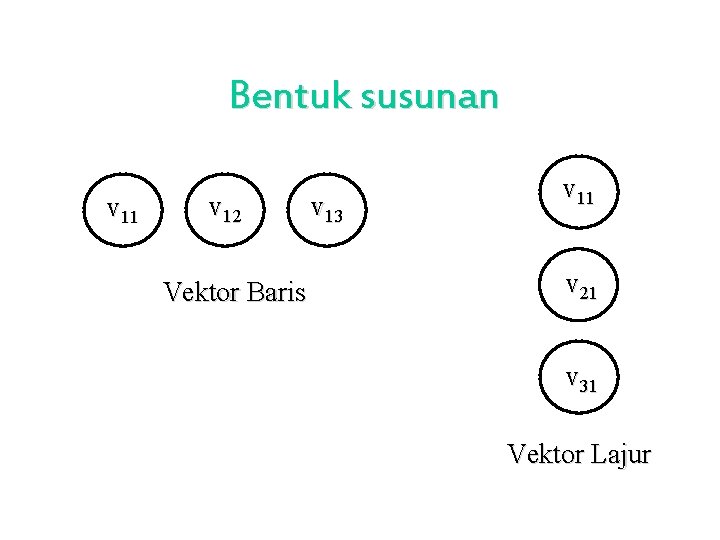
Bentuk susunan v 11 v 12 Vektor Baris v 13 v 11 v 21 v 31 Vektor Lajur

Notasi Vektor baris vb = ( v 11 v 12 v 13 ) v = (v 11 v 12 v 13 ) 1 x 3 v’ = (v 11 v 12 v 13 ) Vektor lajur vl = v 11 v 21 v 31 v = v 11 3 x 1 v 21 v 31 v = v 11 v 21 v 31

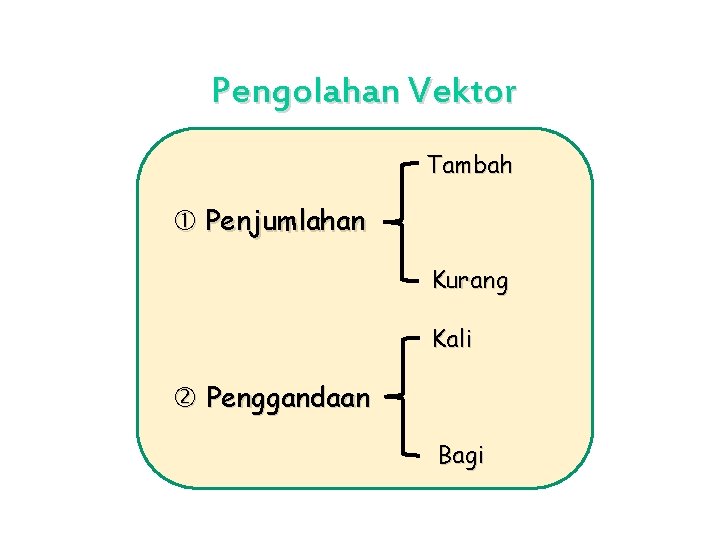
Pengolahan Vektor Tambah Penjumlahan Kurang Kali Penggandaan Bagi

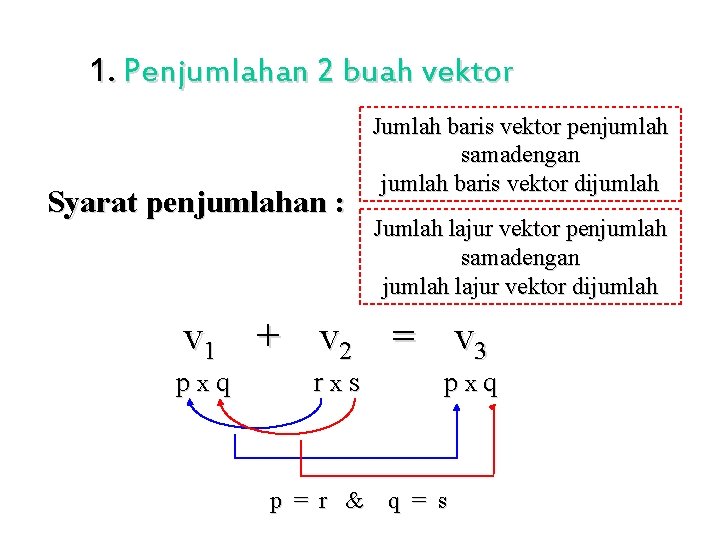
1. Penjumlahan 2 buah vektor Syarat penjumlahan : Jumlah baris vektor penjumlah samadengan jumlah baris vektor dijumlah Jumlah lajur vektor penjumlah samadengan jumlah lajur vektor dijumlah v 1 + v 2 = v 3 pxq rxs pxq p = r & q = s

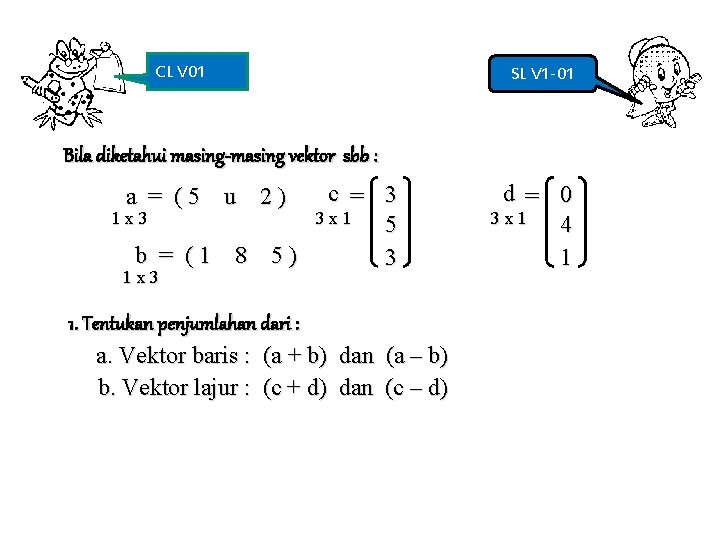
CL V 01 SL V 1 -01 Bila diketahui masing-masing vektor sbb : c = 3 3 x 1 1 x 3 5 b = (1 8 5) 3 a = (5 u 2) 1 x 3 1. Tentukan penjumlahan dari : a. Vektor baris : (a + b) dan (a – b) b. Vektor lajur : (c + d) dan (c – d) d = 0 3 x 1 4 1

Penyelesaian 1 : a. Penjumlahan vektor baris a + b = ( 5 u 2 ) + ( 1 8 5 ) = ( 6 u+8 7) (1 x 3) a – b = ( 5 u 2 ) − ( 1 8 5 ) = ( 4 u-8 -3) (1 x 3) b. Penjumlahan vektor lajur c+d= 3 x 1 3 5 3 + 0 4 1 = 3 9 4 c−d= 3 x 1 3 5 3 + 0 4 1 = 3 1 2

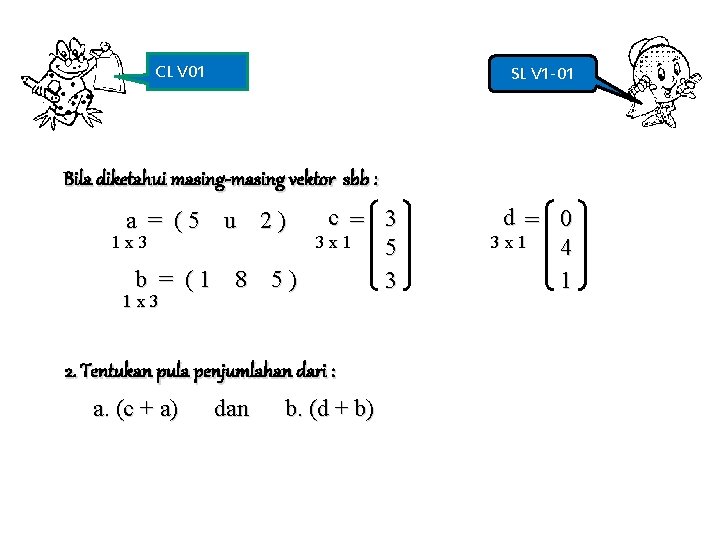
CL V 01 SL V 1 -01 Bila diketahui masing-masing vektor sbb : c = 3 3 x 1 1 x 3 5 b = (1 8 5) 3 a = (5 u 2) 1 x 3 2. Tentukan pula penjumlahan dari : a. (c + a) dan b. (d + b) d = 0 3 x 1 4 1

Penyelesaian 2 : a. Penjumlahan dari vektor lajur & vektor baris : (c + a) = 3 ( 5 u 2 ) Tidak dapat dilakukan karena : 1 x 3 ü Jumlah baris vektor a ≠ jumlah 5 baris vektor c ü Jumlah lajur vektor a ≠ jumlah lajur vektor c 3 3 x 1 b. Penjumlahan dari vektor baris & vektor lajur : (b - d) = ( 1 8 5 ) 0 1 x 3 4 1 3 x 1 Tidak dapat dilakukan karena : ü Jumlah baris vektor d ≠ jumlah baris vektor b ü Jumlah lajur vektor d ≠ jumlah lajur vektor b

2. Penggandaan 2 buah vektor Syarat umum penggandaan : vektor 1 x vektor 2 (baris 2 x lajur 2) (baris 1 x lajur 1) sama jumlahnya Hasil penggandaan : * vektor baris x vektor lajur = skalar * vektor lajur x vektor baris = st matriks Matriks segi Matriks tak segi

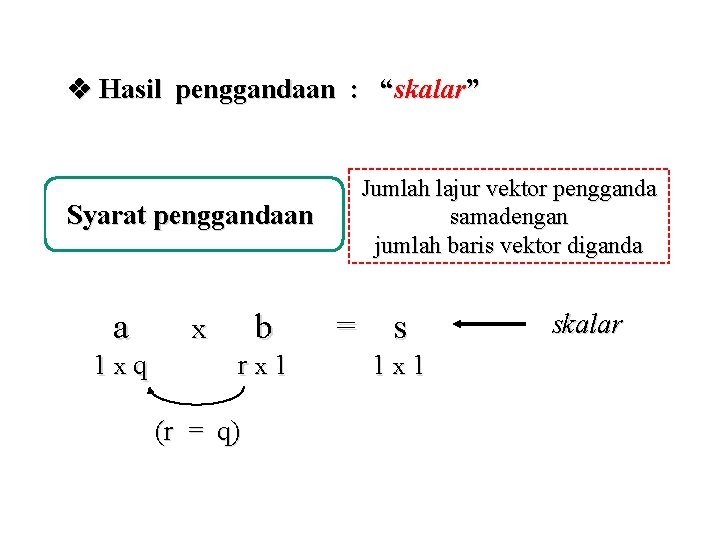
Hasil penggandaan : “skalar” Syarat penggandaan a 1 xq b x rx 1 (r = q) Jumlah lajur vektor pengganda samadengan jumlah baris vektor diganda = s 1 x 1 skalar

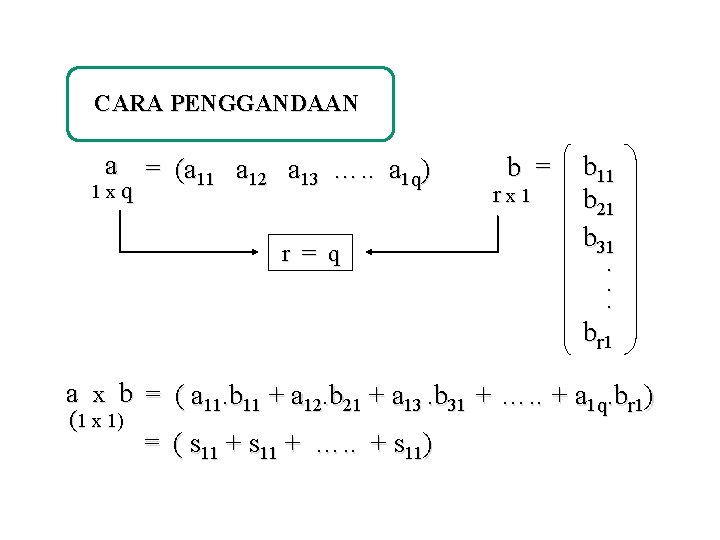
CARA PENGGANDAAN a = (a 11 a 12 a 13 …. . a 1 q) 1 xq r = q b = rx 1 b 11 b 21 b 31. . . br 1 a x b = ( a 11. b 11 + a 12. b 21 + a 13. b 31 + …. . + a 1 q. br 1) (1 x 1) = ( s 11 + …. . + s 11)

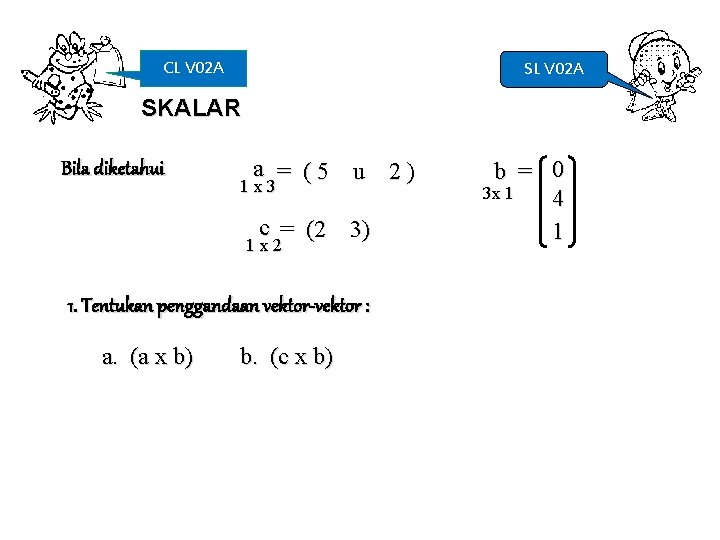
CL V 02 A SKALAR Bila diketahui a = (5 u 2) 1 x 3 c = (2 3) 1 x 2 1. Tentukan penggandaan vektor-vektor : a. (a x b) b. (c x b) b = 0 3 x 1 4 1

Penyelesaian 1 : a. a x b = (5 u 2) 0 1 x 3 3 x 1 4 1 = (5 x 0) + (u x 4) + (2 x 1) = 4 u +2 b. c x b = ( 2 3 ) 0 1 x 2 3 x 1 4 1 Tidak dapat dilakukan karena : ü Jumlah baris vektor b ≠ jumlah lajur vektor c

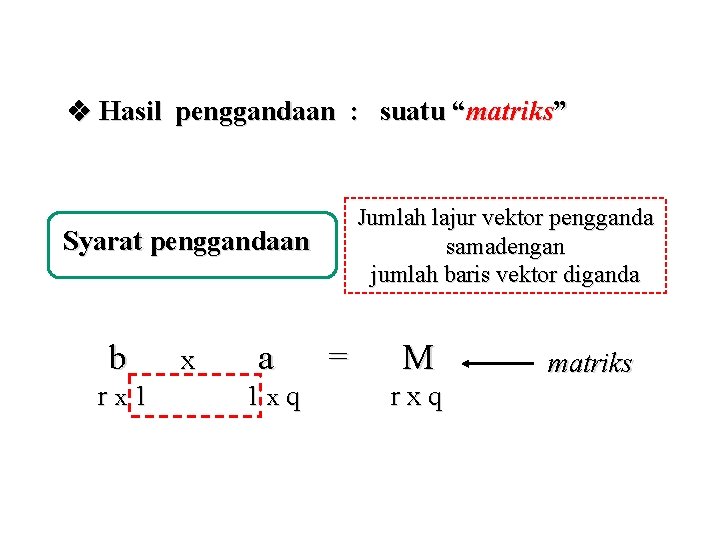
Hasil penggandaan : suatu “matriks” Jumlah lajur vektor pengganda samadengan jumlah baris vektor diganda Syarat penggandaan b rx 1 x a 1 xq = M rxq matriks

b x a rx 1 1 xq = = b 11 b 21 b 31. . . br 1 ( a 11 a 12 a 13 …. . a 1 q) b 11. a 11 b 21. a 11 b 31. a 11. . . br 1. a 11 CARA PENGGANDAAN b 11. a 12 b 11. a 13 …. b 11. a 1 q b 21. a 12 b 21. a 13 …. b 21. a 1 q b 31. a 12 b 31. a 13 …. b 31. a 1 q. . br 1. a 12 br 1. a 13 …. br 1. a 1 q

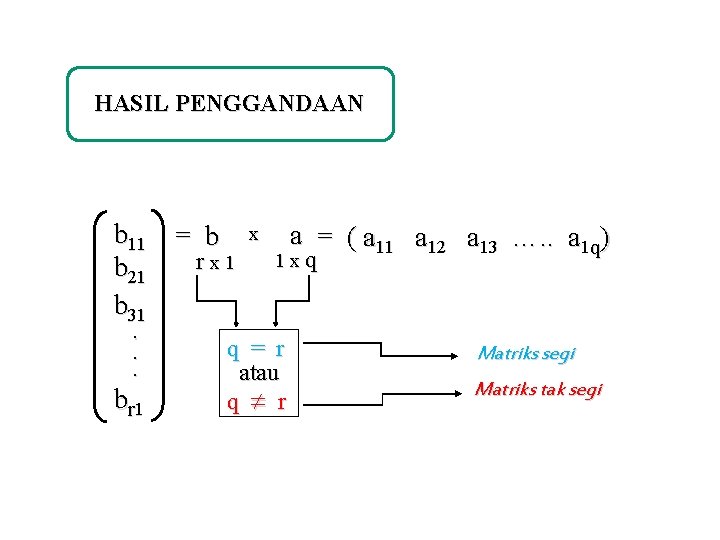
HASIL PENGGANDAAN b 11 b 21 b 31. . . br 1 = b x rx 1 a = ( a 11 a 12 a 13 …. . a 1 q) 1 xq q = r atau q r Matriks segi Matriks tak segi

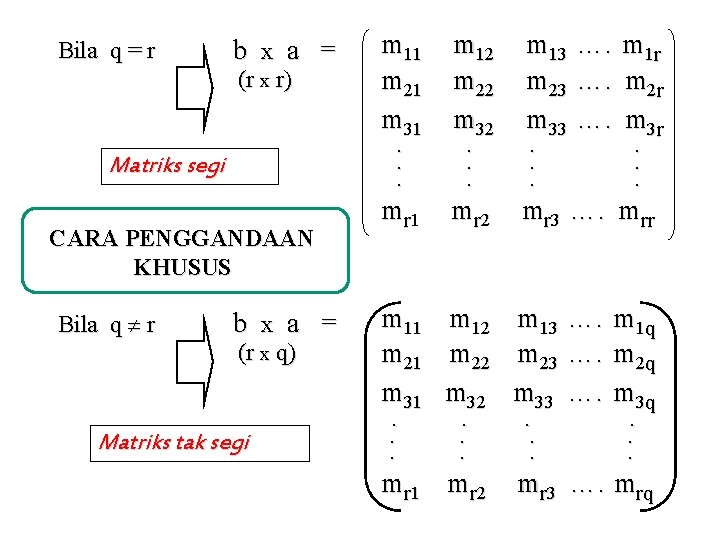
Bila q = r b x a = (r x r) Matriks segi CARA PENGGANDAAN KHUSUS Bila q r b x a = (r x q) Matriks tak segi m 11 m 21 m 31. . . m r 1 m 12 m 13 …. m 1 r m 22 m 23 …. m 2 r m 32 m 33 …. m 3 r. . mr 2 mr 3 …. mrr m 11 m 21 m 31. . . m r 1 m 12 m 22 m 32. . . m r 2 m 13 m 23 m 33. . . m r 3 …. m 1 q …. m 2 q …. m 3 q. . . …. mrq

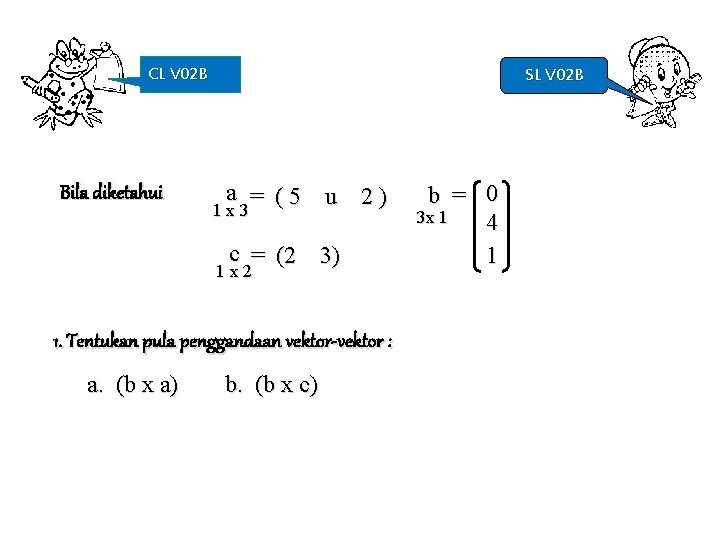
CL V 02 B Bila diketahui SL V 02 B a = (5 u 2) 1 x 3 c = (2 3) 1 x 2 1. Tentukan pula penggandaan vektor-vektor : a. (b x a) b. (b x c) b = 0 3 x 1 4 1

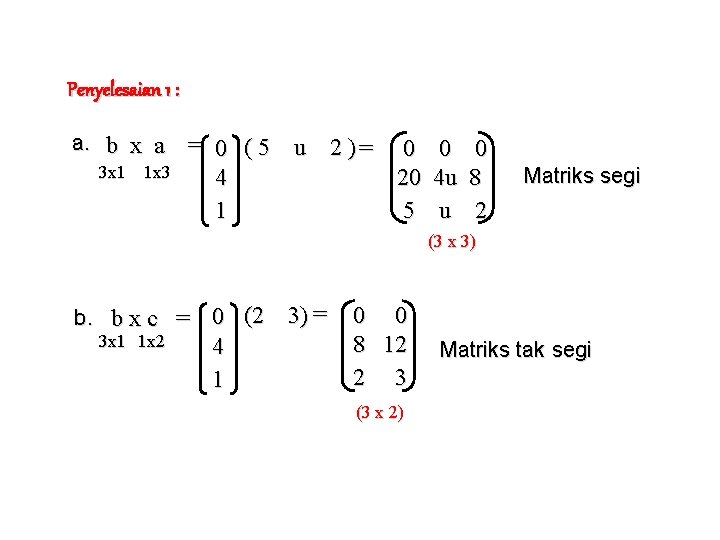
Penyelesaian 1 : a. b x a 3 x 1 1 x 3 = 0 ( 5 u 2 )= 0 0 4 20 4 u 1 5 u 0 8 2 Matriks segi (3 x 3) b. b x c = 0 (2 3 x 1 1 x 2 4 1 3) = 0 0 8 12 2 3 (3 x 2) Matriks tak segi

Penggandaan skalar thd st vektor thd skalar Mengacu pada syarat penggandaan 2 buah vektor, diperoleh : Skalar s x vektor baris x = s(vektor baris x) = sx 11 sx 12 sx 13 …. . sx 1 l Vektor lajur x x skalar s = (vektor lajur x)s = x 11 s x 21 s x 31 s. . xb 1 s “Dimensi hasil penggandaan tergantung dimensi vektornya”

CL V 02 C Skalar S = 5 Diketahui bahwa : Vektor baris b = (1 3 5) 1. Tentukan penggandaan untuk : a. (S x b) b. (b x S) Vektor lajur l = 2 4 6 Penyelesaian 1 : a. S x b = 5 X (1 3 5) = (5 15 25) 1 x 1 1 x 3 b. b x S = (1 3 5) x 5 = Tidak dapat dilakukan karena jumlah 1 x 3 1 x 1 baris pada skalar s (= 1) ≠ jumlah lajur pada vektor b (= 3)

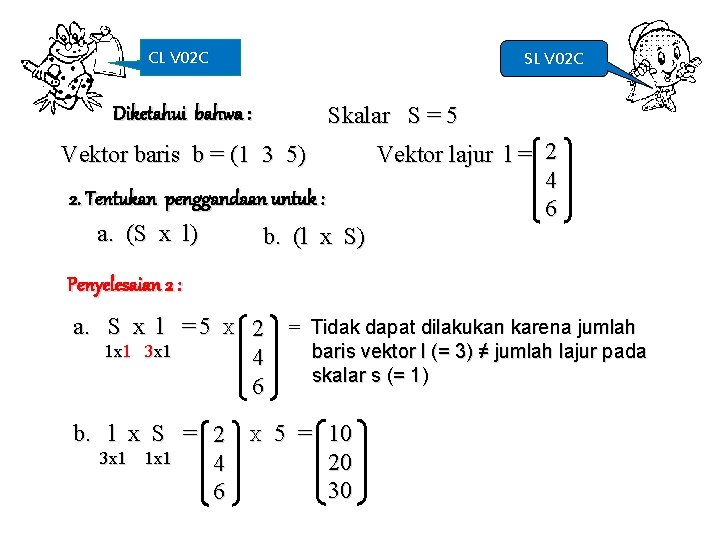
CL V 02 C Skalar S = 5 Diketahui bahwa : Vektor baris b = (1 3 5) 2. Tentukan penggandaan untuk : a. (S x l) b. (l x S) Vektor lajur l = 2 4 6 Penyelesaian 2 : a. S x l = 5 X 1 x 1 3 x 1 b. l x S = 2 3 x 1 1 x 1 4 6 2 4 6 X = Tidak dapat dilakukan karena jumlah baris vektor l (= 3) ≠ jumlah lajur pada skalar s (= 1) 5 = 10 20 30

Vektor dalam geometrik Y y P(x, y) = penjumlahan 2 buah vekor 0 x X (x, y) = (x , 0) + (0 , y) ( x , y ) = x (1 , 0) + y ( 0 , 1) • penyusunan kombinasi linier

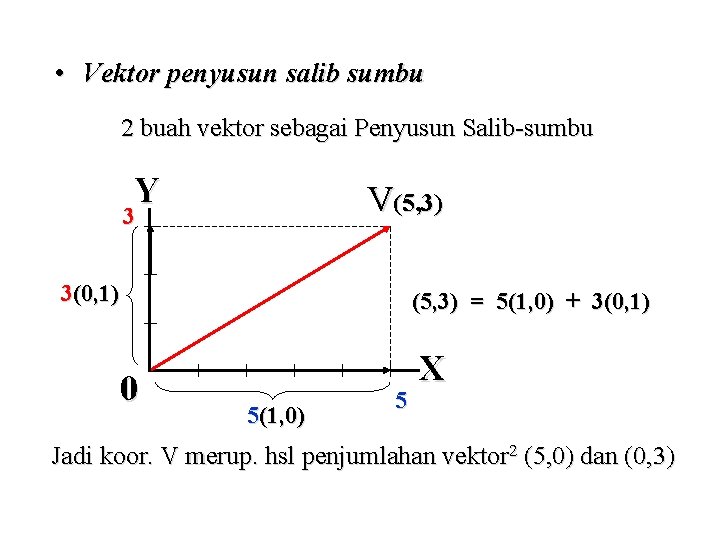
• Vektor penyusun salib sumbu 2 buah vektor sebagai Penyusun Salib-sumbu Y V(5, 3) 3 3(0, 1) 0 (5, 3) = 5(1, 0) + 3(0, 1) 5(1, 0) 5 X Jadi koor. V merup. hsl penjumlahan vektor 2 (5, 0) dan (0, 3)

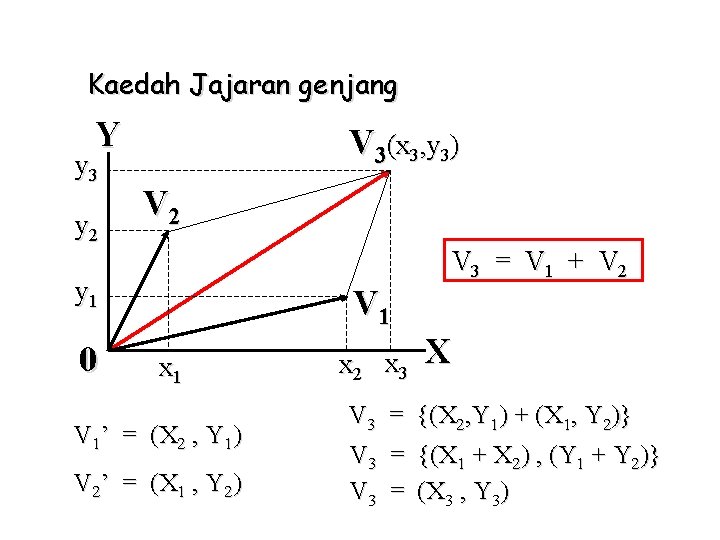
Kaedah Jajaran genjang Y y 3 y 2 V 3(x 3, y 3) V 2 V 3 = V 1 + V 2 y 1 0 V 1 x 1 V 1’ = (X 2 , Y 1) V 2’ = (X 1 , Y 2) x 2 x 3 V 3 V 3 = = = X {(X 2, Y 1) + (X 1, Y 2)} {(X 1 + X 2) , (Y 1 + Y 2)} (X 3 , Y 3)

V 3 = (X 3 , Y 3) Jadi vektor V 3 diperoleh dari : * x 3 kali vektor (1, 0) yg berimpit dgn sumbu X * y 3 kali vektor (0, 1) yg berimpit dgn sumbu Y Vektor (1, 0) & vektor (0, 1) masing 2 terbobot oleh kofaktor x sebesar x 3 dan kofaktor y sebesar y 3

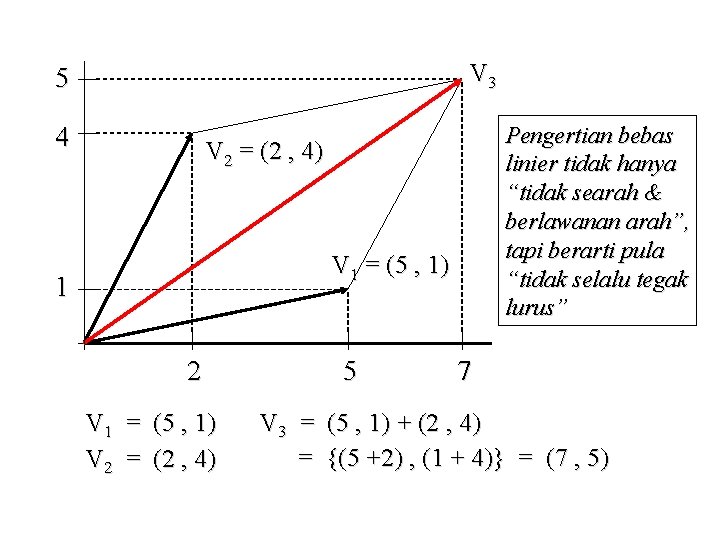
V 3 5 4 Pengertian bebas linier tidak hanya “tidak searah & berlawanan arah”, tapi berarti pula “tidak selalu tegak lurus” V 2 = (2 , 4) V 1 = (5 , 1) 1 2 V 1 = (5 , 1) V 2 = (2 , 4) 5 7 V 3 = (5 , 1) + (2 , 4) = {(5 +2) , (1 + 4)} = (7 , 5)

Pengembangan pada 3 dimensi Vektor (x, y, z) dapat pula berupa kombinasi linier dari 3 vektor yang bebas terhadap sesamanya (x, y, z) = x (1, 0, 0) + y (0, 1, 0) + z (0, 0, 1) (2, 3, 4) = 2 (1, 0, 0) + 3 (0, 1, 0) + 4 (0, 0, 1)

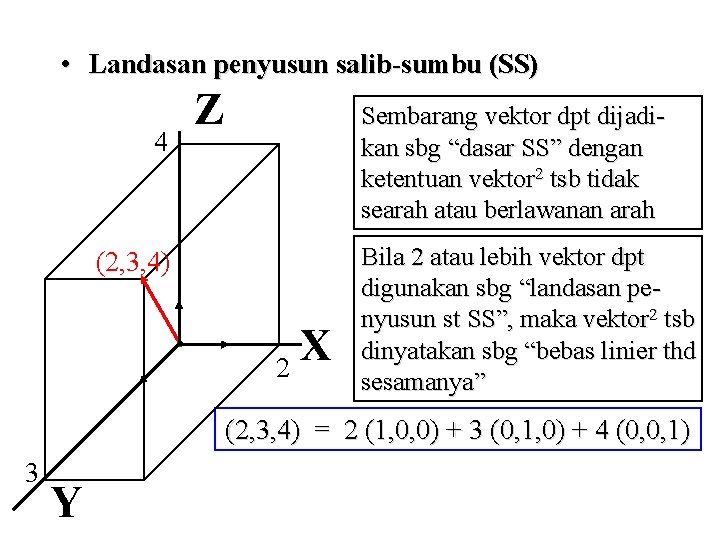
• Landasan penyusun salib-sumbu (SS) 4 Z Sembarang vektor dpt dijadikan sbg “dasar SS” dengan ketentuan vektor 2 tsb tidak searah atau berlawanan arah (2, 3, 4) X 2 Bila 2 atau lebih vektor dpt digunakan sbg “landasan penyusun st SS”, maka vektor 2 tsb dinyatakan sbg “bebas linier thd sesamanya” (2, 3, 4) = 2 (1, 0, 0) + 3 (0, 1, 0) + 4 (0, 0, 1) 3 Y

CL V 03 SL V 03 1. Koordinat titik P (5, 3) dibentuk oleh vektor (5, 0) dan (0, 3). Bila unsur vektor (5, 0) diubah menjadi (3, 1) dan unsur vektor (0, 3) diubah menjadi (2, 2), tentukan : a. Kofaktor masing-masing vektor yang baru b. Buat ilustrasinya Penyelesaian 1 : a. Kofaktor masing-masing vektor (5, 3) = (5, 0) + (0, 3) (5, 3) = (3, 1) + (2, 2) (5, 3) = 5(1, 0) + 3(0, 1). . (5, 3) = x (3, 1) + y (2, 2)

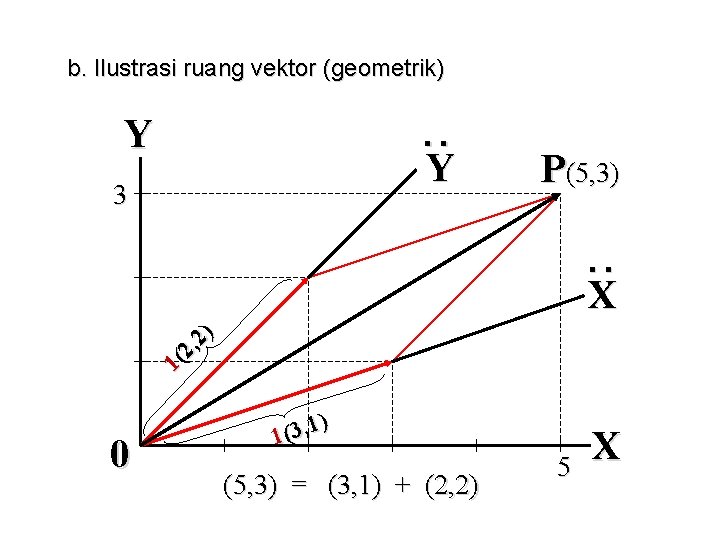
b. Ilustrasi ruang vektor (geometrik) Y . . Y 3 P(5, 3). . X 2) , 2 ( 1 0 1) , 3 ( 1 (5, 3) = (3, 1) + (2, 2) 5 X

CL V 03 SL V 03 2. Koordinat titik P terhadap salib-sumbu berupa vektor (2, 6). Tentukan koordinat titik P tsb (Kx dan Ky) terhadap vektor-vektor penyusun salib-sumbu yang baru (0, 1) dan (2, 4).

• Landasan ruang vektor Penyusunan 2 vektor atau lebih membentuk suatu matriks Katakan saja ada 3 buah vektor yaitu (1 -1 2) 1 -1 2 0 1 3 1 1 3 matriks (0 1 3) ? (1 1 3) Apakah ketiga tsb dapat digunakan sebagai landasan dalam membentuk ruang vektor Maksudnya ?

Maksudnya : Landasan : vektor yang dapat digunakan sebagai salib-sumbu dalam membentuk ruang vektor (geometrik). Vektor yang dapat digunakan sebagai landasan, bukan merupakan vektor nol. Ruang vektor dimaksud : bidang yang dibatasi 2 vektor (bidang datar; 2 dimensi), bidang yang dibatasi 3 vektor atau lebih (bidang ruang; 3 dimensi atau lebih). Tiga vektor atau lebih yang akan digunakan sebagai landasan, ada kemungkinan diantaranya merupakan vektor nol atau keseluruhannya merupakan vektor nol. Uraian lebih lanjut ditelaah dalam pengolahan matriks.

Norma Vektor v’ = (v 1 v 2 v 3 …. . vn) v’v = (v 1 v 2 v 3. …. vn) v 1 v 2 v 3. . vn = (v 12 + v 22 + v 32 + …. + vn 2)

|| v || = √ (v 12 + v 22 + v 32 + …. + vn 2) v’v bila || v || = 1 norma vektor satuan Harga norma vektor v merupakan pula panjang vektor v.

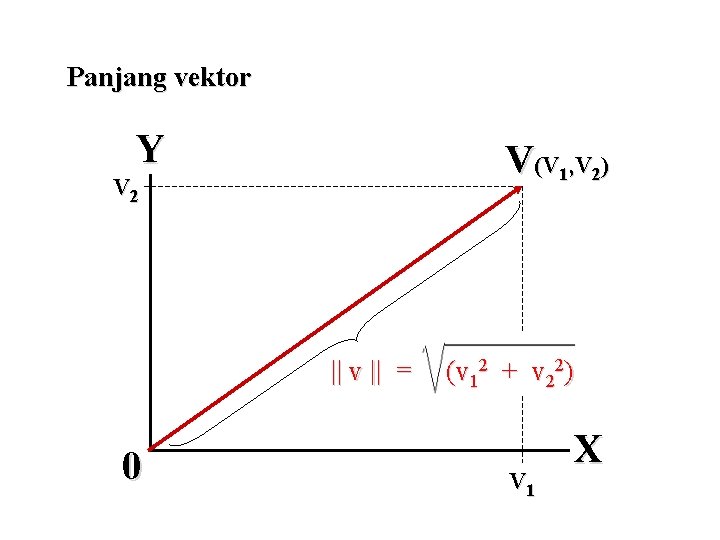
Panjang vektor Y V(V 1, V 2) V 2 || v || = 0 (v 12 + v 22) V 1 X

Sudut antara 2 vektor cos = cos x’ y || x || || y || = 0 jika x’y = 0 = 900 Jadi vektor x dan vektor y saling tegak-lurus maka sudut yang dibentuk sebesar 900

CL V 04 - SL V 04 Vektor-vektor penyusun salib-sumbu terdiri dari absis dan ordinat. a. sebagai absis (-1, 1) dan ordinat (1, 3) b. sebagai absis (1, 1) dan ordinat (1, -1) c. sebagai absis (1, 1) dan ordinat (-1, 1) d. sebagai absis (1, 1) dan ordinat (1, -3) Ilustrasikan masing-masing pasangan absis dan ordinat di atas. Tentukan besar sudut yang dibentuknya

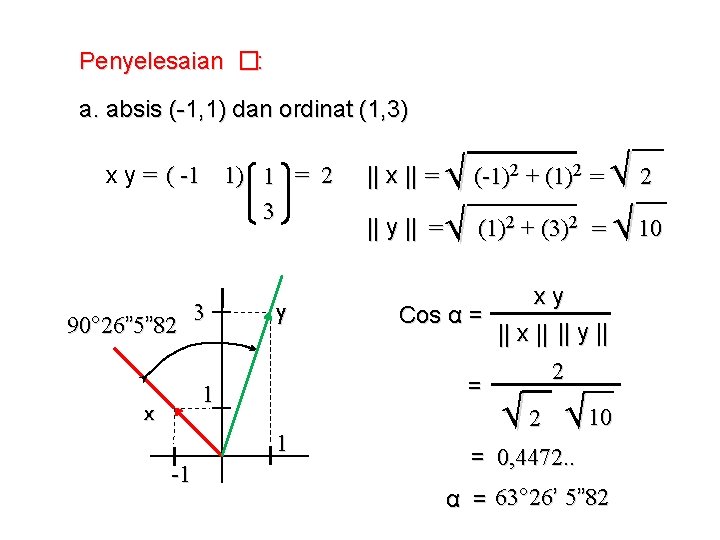
Penyelesaian �: a. absis (-1, 1) dan ordinat (1, 3) x y = ( -1 1) 1 = 2 3 3 90° 26” 5” 82 y 1 -1 √ 2 = √ 10 (-1)2 + (1)2 = xy Cos α = || x || || y || = 1 x √ || y || = √ (1)2 + (3)2 || x || = 2 √ 10 = 0, 4472. . α = 63° 26’ 5” 82

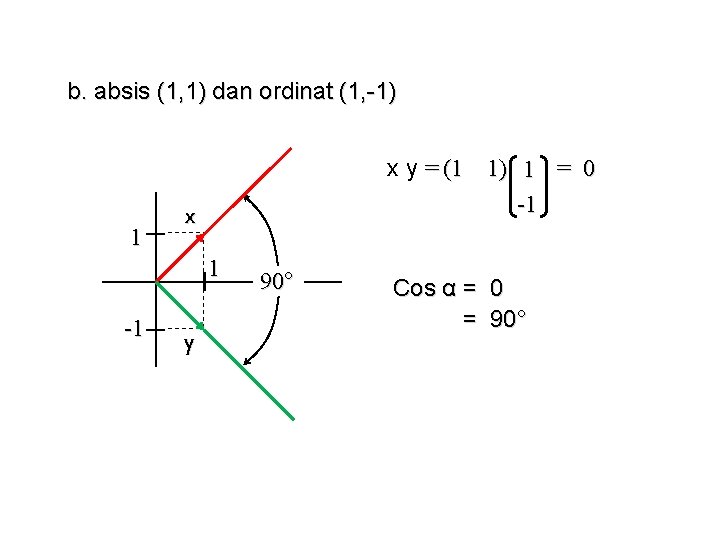
b. absis (1, 1) dan ordinat (1, -1) 1 x y = (1 1) 1 = 0 -1 x 1 -1 y 90° Cos α = 0 = 90°

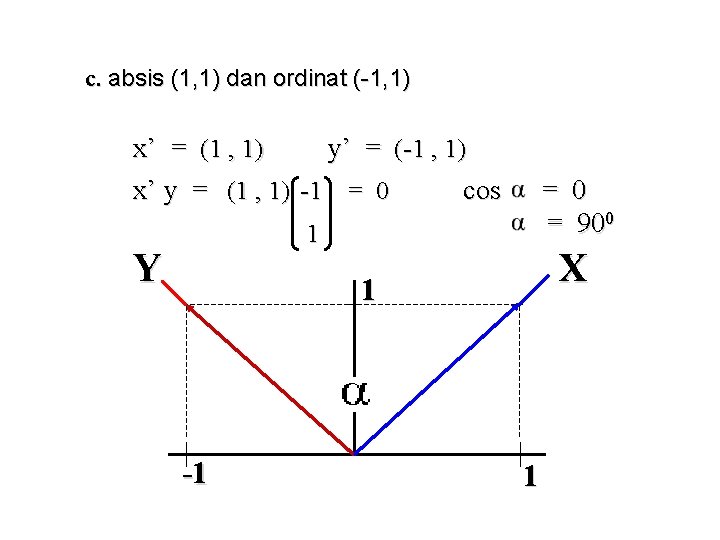
c. absis (1, 1) dan ordinat (-1, 1) x’ = (1 , 1) y’ = (-1 , 1) x’ y = (1 , 1) -1 = 0 cos = 0 = 900 1 Y X 1 -1 1

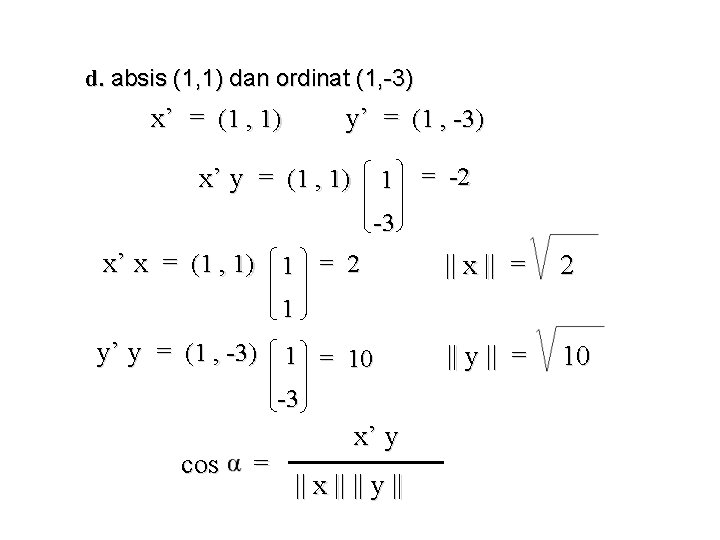
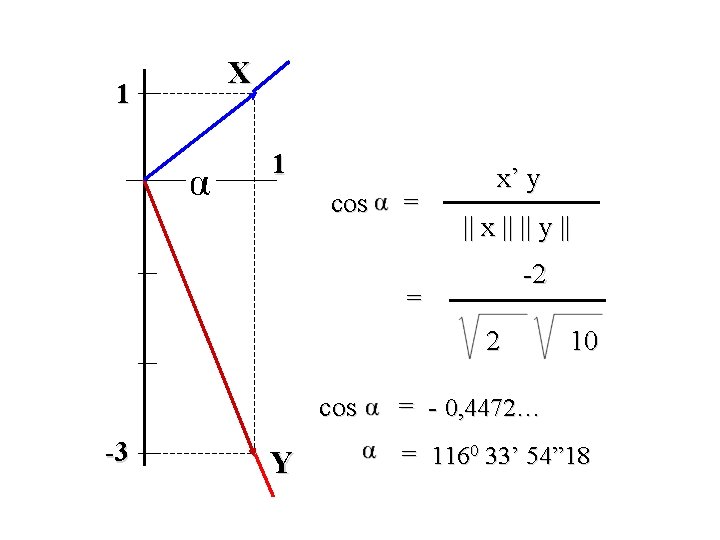
1 X 1 cos = x’ y || x || || y || -2 = 2 cos -3 Y 10 = - 0, 4472… = 1160 33’ 54” 18

Kedua vektor penyusun salib-sumbu terdiri dari K 1 = (2, 3, 6) dan K 2 = (3, 1, 4) Ilustrasikan vektor penyusun tsb Tentukan besar sudut yang dibentuknya Penyelesaian �: cos k’ 1 = (2 , 3 , 6) k’ 1 k 2 = || k 1 || || k 2 || (2 3 6) cos k’ 2 = (5 , 2 , 3) 5 2 3 = (22 + 32 + 62) (52 + 22 + 32)

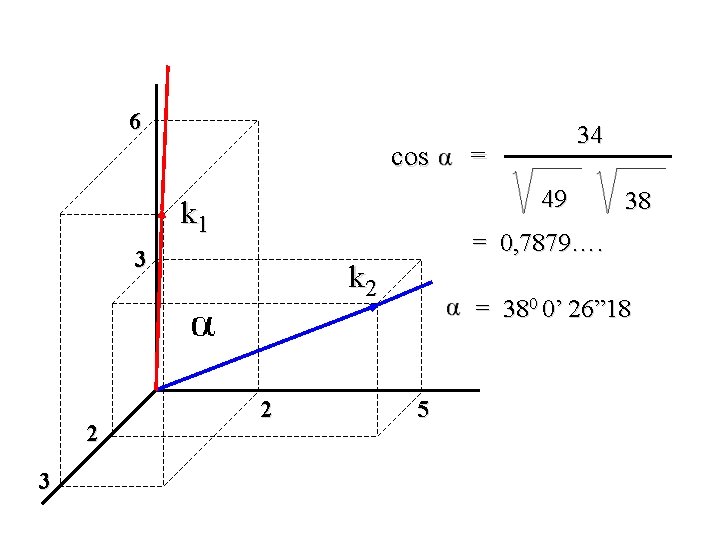
6 cos 38 = 0, 7879…. 3 3 = 49 k 1 2 34 k 2 2 = 380 0’ 26” 18 5