5 8 Curve Fitting with Quadratic Models Objectives

5 -8 Curve Fitting with Quadratic Models Objectives Use quadratic functions to model data. Use quadratic models to analyze and predict. Holt Algebra 2

5 -8 Curve Fitting with Quadratic Models Vocabulary quadratic model quadratic regression Holt Algebra 2

5 -8 Curve Fitting with Quadratic Models Recall that you can use differences to analyze patterns in data. For a set of ordered parts with equally spaced x-values, a quadratic function has constant nonzero second differences, as shown below. Holt Algebra 2

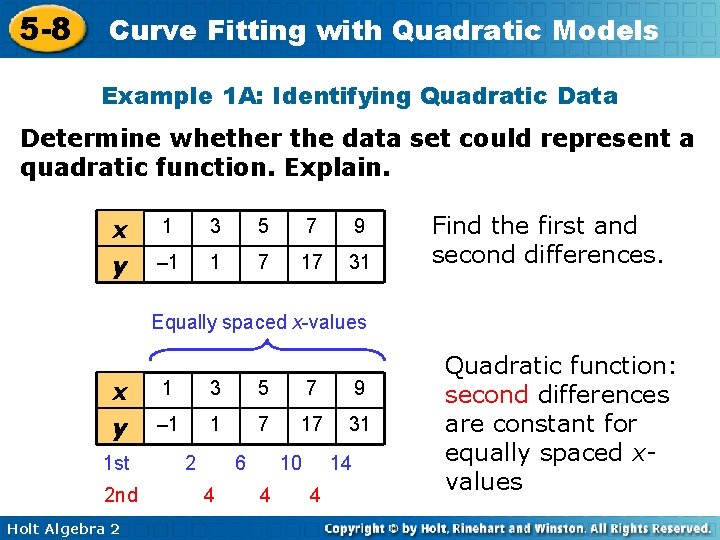
5 -8 Curve Fitting with Quadratic Models Example 1 A: Identifying Quadratic Data Determine whether the data set could represent a quadratic function. Explain. x y 1 3 5 7 9 – 1 1 7 17 31 Find the first and second differences. Equally spaced x-values x y 1 st 2 nd Holt Algebra 2 1 3 5 7 9 – 1 1 7 17 31 2 6 4 10 4 14 4 Quadratic function: second differences are constant for equally spaced xvalues

5 -8 Curve Fitting with Quadratic Models Example 1 B Determine whether the data set could represent a quadratic function. Explain. x y 10 9 8 7 6 6 8 10 12 14 Find the first and second differences. Equally spaced x-values x y 1 st 2 nd Holt Algebra 2 10 9 8 7 6 6 8 10 12 14 2 2 0 2 0 Not a quadratic function: first differences are constant so the function is linear.

5 -8 Curve Fitting with Quadratic Models Example 2: Writing a Quadratic Function from Data Write a quadratic function that fits the points (1, – 5), (3, 5) and (4, 16). Use each point to write a system of equations to find a, b, and c in f(x) = ax 2 + bx + c. (x, y) (1, – 5) f(x) = ax 2 + bx + c – 5 = a(1)2 + b(1) + c System in a, b, c 1 a + b + c = – 5 (3, 5) 5 = a(3)2 + b(3) + c 9 a + 3 b + c = 5 2 (4, 16) 16 = a(4)2 + b(4) + c 16 a + 4 b + c = 16 3 Holt Algebra 2 1

5 -8 Curve Fitting with Quadratic Models Example 2 Continued Subtract equation 1 to get 2 1 4 2 4 by. 9 a + 3 b + c = 5 a + b + c = – 5 8 a + 2 b + 0 c = 10 Holt Algebra 2 Subtract equation 3 by equation 1 to get 5. 16 a + 4 b + c = 16 a + b + c = – 5 3 1 5 15 a + 3 b + 0 c = 21

5 -8 Curve Fitting with Quadratic Models Example 2 Continued Solve equation elimination. 5 4 4 and equation 2(15 a + 3 b = 21) – 3(8 a + 2 b = 10) 5 for a and b using 30 a + 6 b = 42 – 24 a – 6 b = – 30 6 a + 0 b = 12 a =2 Holt Algebra 2 Multiply by 2. Multiply by – 3. Subtract. Solve for a.

5 -8 Curve Fitting with Quadratic Models Example 2 Continued Substitute 2 for a into equation get b. 4 or equation 5 to 8(2) +2 b = 10 15(2) +3 b = 21 2 b = – 6 b = – 3 3 b = – 9 Holt Algebra 2 b = – 3

5 -8 Curve Fitting with Quadratic Models Example 2 Continued Substitute a = 2 and b = – 3 into equation solve for c. 1 to (2) +(– 3) + c = – 5 – 1 + c = – 5 c = – 4 Write the function using a = 2, b = – 3 and c = – 4. f(x) = ax 2 + bx + c Holt Algebra 2 f(x)= 2 x 2 – 3 x – 4

5 -8 Curve Fitting with Quadratic Models A quadratic model is a quadratic function that represents a real data set. Models are useful for making estimates. Holt Algebra 2

5 -8 Curve Fitting with Quadratic Models Lesson Quiz: Part I Determine whether each data set could represent a quadratic function. 1. x y 5 6 7 8 9 5 8 13 21 34 2. x y 2 3 4 5 6 1 11 25 43 65 not quadratic 3. Write a quadratic function that fits the points (2, 0), (3, – 2), and (5, – 12). f(x) = –x 2 + 3 x – 2 Holt Algebra 2