5 7 Scale Drawings and Scale Models Lesson

5 -7 Scale Drawings and Scale Models Lesson 7. 5 Scale Drawings Students will be able to understand ratios and proportions in scale drawings. Students will be able to use ratios and proportions with scale. Course 2

Homework (4/17/17) Worksheet: Angle Sum of Triangles and Quadrilateral (front and back) (4/18/17) Complementary and Supplementary Worksheet 2 (4/19/17) Chapter 7 Practice Test (4/20/17) Study Guide, Ch 7 hw packet

5 -7 Scale Drawings and Scale Models Write each fraction in the simplest form. 4 1 1. 48 12 2. 9 135 1 15 Convert the following measurements. 3. 192 inches = 4. 18. 5 feet = 5. 324 inches = Course 2 feet 16 inches 222 feet 27

Ratio • A ratio is a comparison of two quantities

Scale • A scale is a ratio between two sets of measurements. – Examples: • Drawings: ¼ inch = 1 foot • Maps: 1 inch = 250 miles

Scale Drawing (Model) • A scale drawing (model) is a drawing that uses a scale to make an object smaller than (reduction) or larger than (enlargement) the real object.

Scale Factor • A scale factor is a ratio used to enlarge or reduce similar figures. – Examples: enlarging a piece of candy for a drawing…or the Willy Wonka Factory…

The Scale Factor The scale factor is the amount that you enlarge or reduce an object by. Enlarge: A scale factor that is larger than 1 will make the shape get bigger. Reduce: A scale factor that is smaller than 1 but larger than 0 will make the shape get smaller. Remember, the shape of the object does not change, only its size!

The lengths and widths of objects of a scale drawing or model are proportional to the lengths and widths of the actual object.

5 -7 Scale Drawings and Scale Models Example 1: Finding a Scale Factor Identify the scale factor. Room Blueprint Length (in. ) 144 18 Width (in. ) 108 13. 5 blueprint length = 18 144 room length = 1 8 The scale factor is 1. 8 Course 2 Write a ratio using one of the dimensions. Simplify.

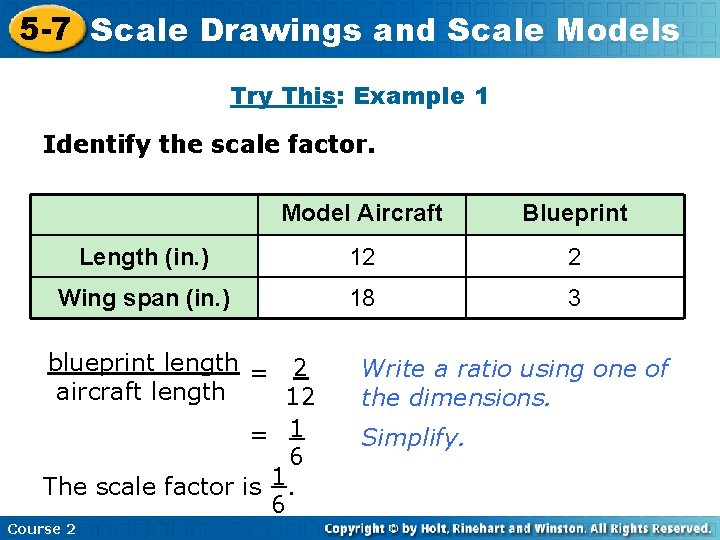
5 -7 Scale Insert Drawings Lesson Title and. Here Scale Models Try This: Example 1 Identify the scale factor. Model Aircraft Blueprint Length (in. ) 12 2 Wing span (in. ) 18 3 blueprint length = 2 aircraft length 12 = 1 6 The scale factor is 1. 6 Course 2 Write a ratio using one of the dimensions. Simplify.

5 -7 Scale Drawings and Scale Models Additional Example 2: Using Scale Factors to Find Unknown Lengths A photograph was enlarged and made into a poster. The poster is 20. 5 inches by 36 inches. The scale 5 factor is 1. Find the size of the photograph. poster = 5 Think: photo 1 36 = 5 L 1 Write a proportion to find the length L. 5 L = 36 Find the cross products. L = 7. 2 Course 2 Divide.

5 -7 Scale Drawings and Scale Models Additional Example 2 Continued A photograph was enlarged and made into a poster. The poster is 20. 5 inches by 36 inches. The scale 5 factor is 1. Find the size of the photograph. poster = 5 Think: photo 1 20. 5 = 5 w 1 Write a proportion to find the width w. 5 w = 20. 5 Find the cross products. w = 4. 1 Divide. The photo is 7. 2 in. long and 4. 1 in. wide. Course 2

5 -7 Scale Drawings and Scale Models Try This: Example 2 Mary’s father made her a dollhouse which was modeled after the blueprint of their home. The blueprint is 24 inches by 45 inches. The scale factor is 1. 5. Find the size of the dollhouse. 1 Think: dollhouse = 1. 5 blueprint 1 L = 1. 5 45 1 Course 2 Write a proportion to find the length l. L = 45 · 1. 5 Find the cross products. L = 67. 5 Multiply.

5 -7 Scale Drawings and Scale Models Try This 2 Continued Mary’s father made her a dollhouse which was modeled after the blueprint of their home. The blueprint is 24 inches by 45 inches. The scale factor is 1. 5. Find the size of the dollhouse. 1 Think: dollhouse = 1. 5 blueprint 1 w = 1. 5 24 1 Write a proportion to find the width w. w = 24 · 1. 5 Find the cross products. Multiply. w = 36 The dollhouse is 67. 5 inches long and 36 inches wide. Course 2

5 -7 Scale Drawings and Scale Models Additional Example 3: Measurement Application On a road map, the distance between Pittsburgh and Philadelphia is 7. 5 inches. What is the actual distance between the cities if the map scale is 1. 5 inches = 60 miles? Let d be the actual distance between the cities. 1. 5 = 7. 5 Write a proportion. 60 d 1. 5 · d = 60 · 7. 5 Find the cross products. 1. 5 d = 450 Multiply. 1. 5 d = 450 Divide. 1. 5 d = 300 The distance between the cities is 300 miles. Course 2

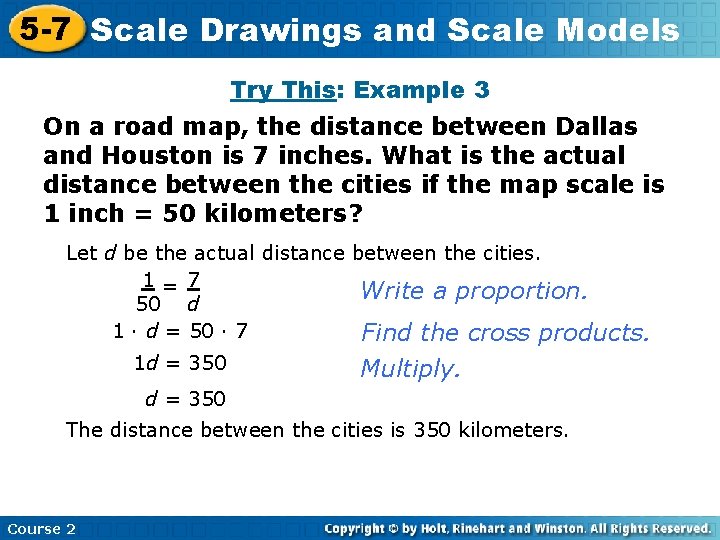
5 -7 Scale Insert Drawings Lesson Title and. Here Scale Models Try This: Example 3 On a road map, the distance between Dallas and Houston is 7 inches. What is the actual distance between the cities if the map scale is 1 inch = 50 kilometers? Let d be the actual distance between the cities. 1= 7 Write a proportion. 50 d 1 · d = 50 · 7 Find the cross products. 1 d = 350 Multiply. d = 350 The distance between the cities is 350 kilometers. Course 2

5 -7 Scale and. Here Scale Models Insert. Drawings Lesson Title Identify the scale factor. 1. Height (in. ) Statue of Liberty Model 1, 824 8 1 228 2. On a scale drawing, a kitchen wall is 6 inches long. 1 The scale factor is. What is the length of the 24 actual wall? 144 inches, or 12 feet Course 2

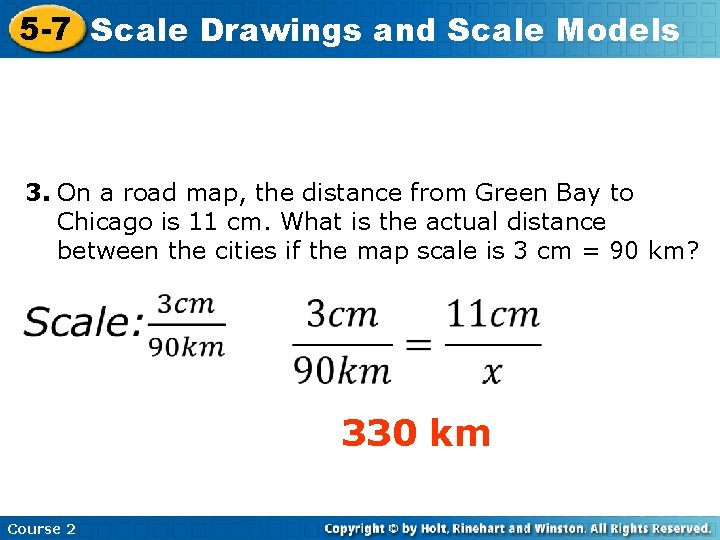
5 -7 Scale and. Here Scale Models Insert. Drawings Lesson Title 3. On a road map, the distance from Green Bay to Chicago is 11 cm. What is the actual distance between the cities if the map scale is 3 cm = 90 km? 330 km Course 2

1. A set of landscape plans shows a flower bed that is 6. 5 inches wide. The scale on the plans is 1 inch = 4 feet. a. What is the width of the actual flower bed? 26 feet b. What is the scale factor? 1 in/4 feet

2. The central chamber of the Lincoln memorial, which features a marble statue of Abraham Lincoln, has a height of 60 feet. Suppose a scale model of the chamber has a height of 4 inches. What is the scale of the model? a. Write a ratio of the height of the model to the actual height of the statue? 60 ft 15 ft 4 in 1 inch = 15 feet b. What is the scale factor? 1 in/15 feet

3. Antonio is designing a room that is 20 feet long and 12 feet wide. Make a scale drawing of the room. Use the scale 0. 25 inches = 4 feet. STEP 1: Find the room’s length on the drawing (let x = length) 20 = x 4 . 25 Length = 1. 25 inches STEP 2: Find the room’s width on the drawing (let w = width) 12 x = 4. 25 Width =. 75 inches

Find the missing lengths The second picture is an enlargement of the first picture. What are the missing lengths? 11. 2 cm 5. 6 cm cm 6. 7 ? 6. 7 cm 13. 4 cm 2. 9 cm 5. 8? cm

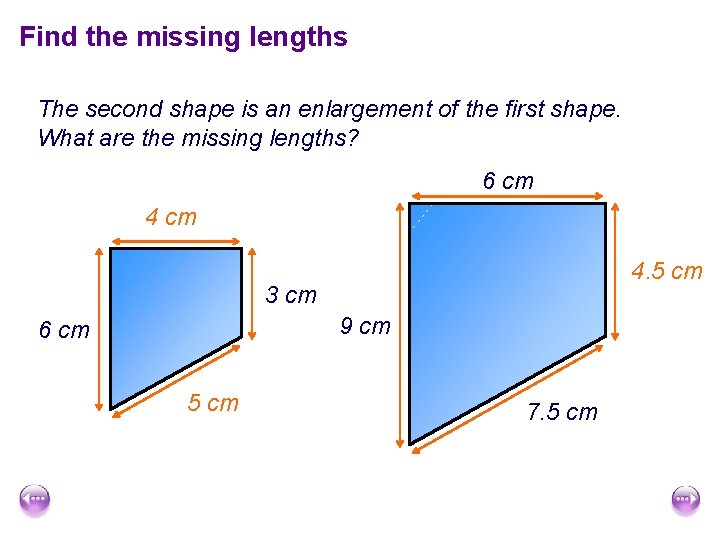
Find the missing lengths The second shape is an enlargement of the first shape. What are the missing lengths? 6 cm 44 cm ? cm 4. 5 ? cm 3 cm 9 cm 6 cm 55? cm cm 7. 5 cm

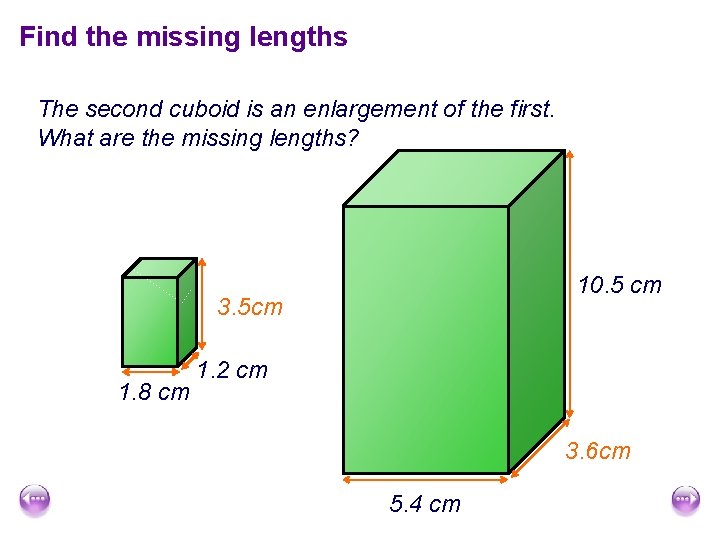
Find the missing lengths The second cuboid is an enlargement of the first. What are the missing lengths? 10. 5 cm 3. 5 ? cm 3. 5 cm 1. 8 cm 1. 2 cm 3. 6 ? cm 5. 4 cm

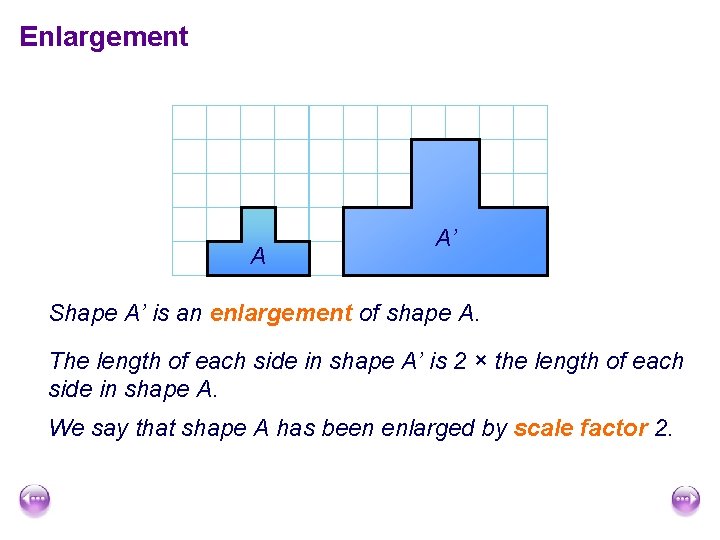
Enlargement A A’ Shape A’ is an enlargement of shape A. The length of each side in shape A’ is 2 × the length of each side in shape A. We say that shape A has been enlarged by scale factor 2.

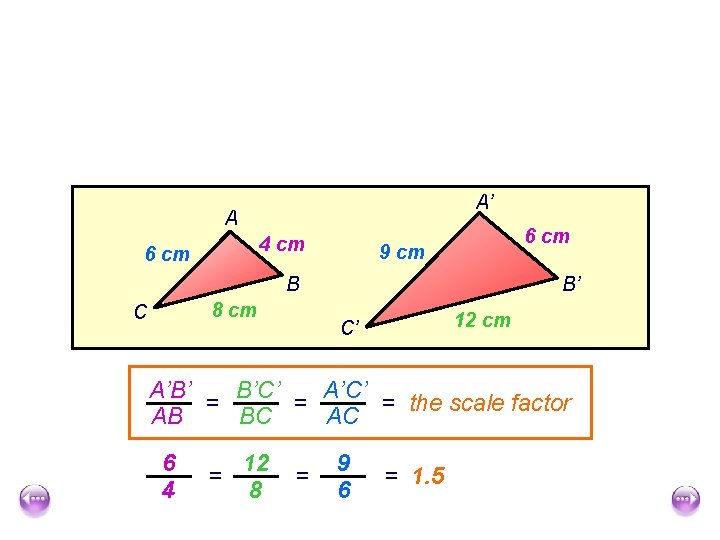
A’ A 4 cm 6 cm 9 cm B 8 cm C B’ 12 cm C’ A’B’ B’C’ A’C’ = = = the scale factor AB BC AC 6 4 12 = 8 = 9 6 = 1. 5

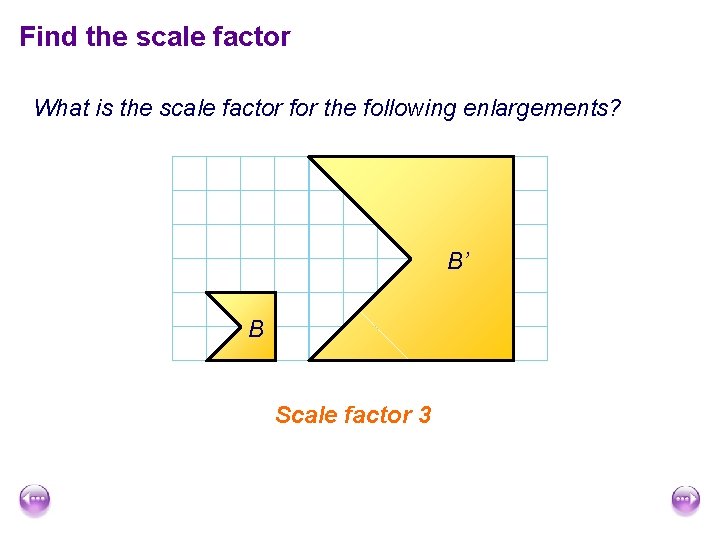
Find the scale factor What is the scale factor for the following enlargements? B’ B Scale factor 3

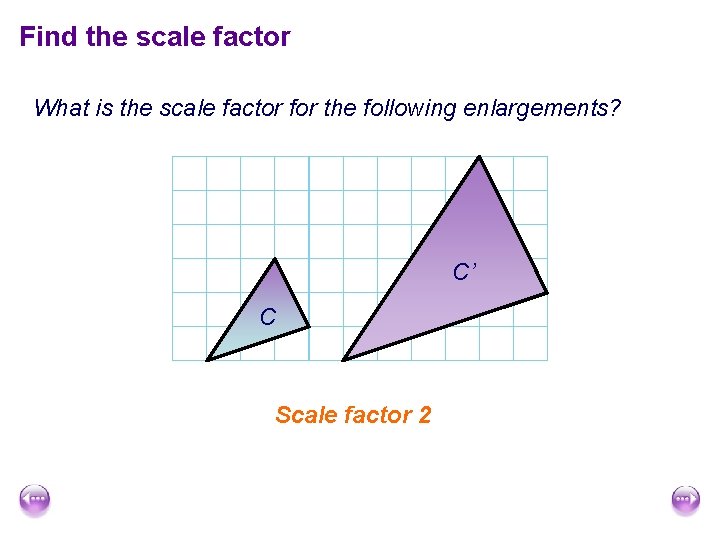
Find the scale factor What is the scale factor for the following enlargements? C’ C Scale factor 2

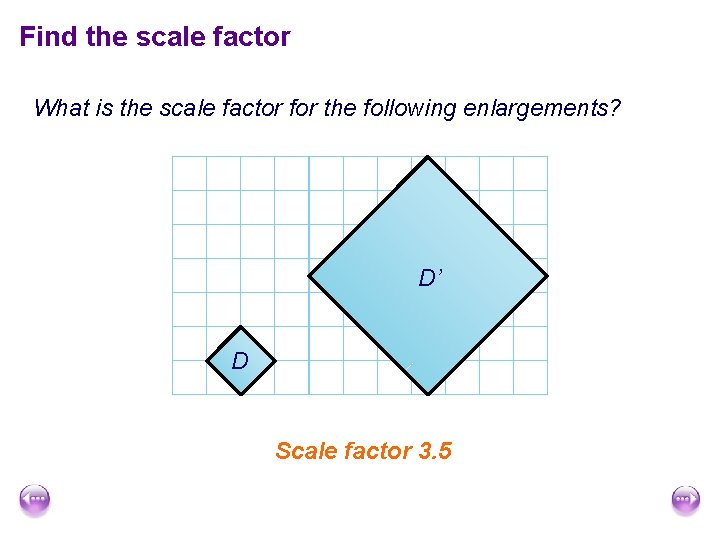
Find the scale factor What is the scale factor for the following enlargements? D’ D Scale factor 3. 5

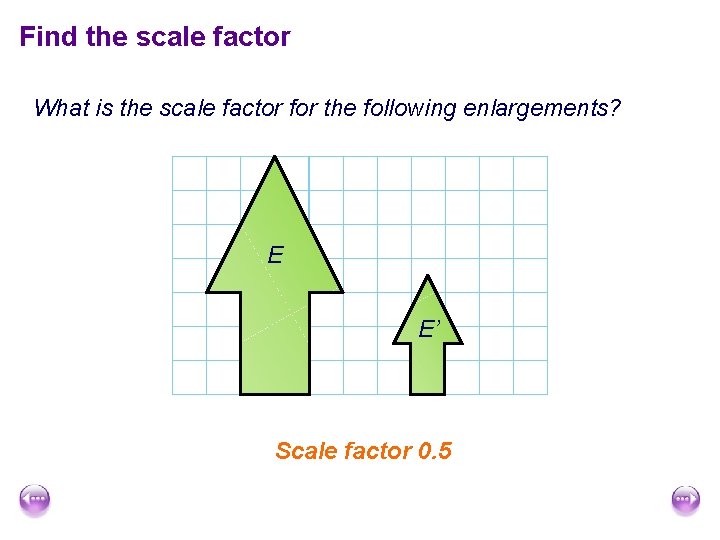
Find the scale factor What is the scale factor for the following enlargements? E E’ Scale factor 0. 5