5 7 Kosi hitac 1 2 3 4


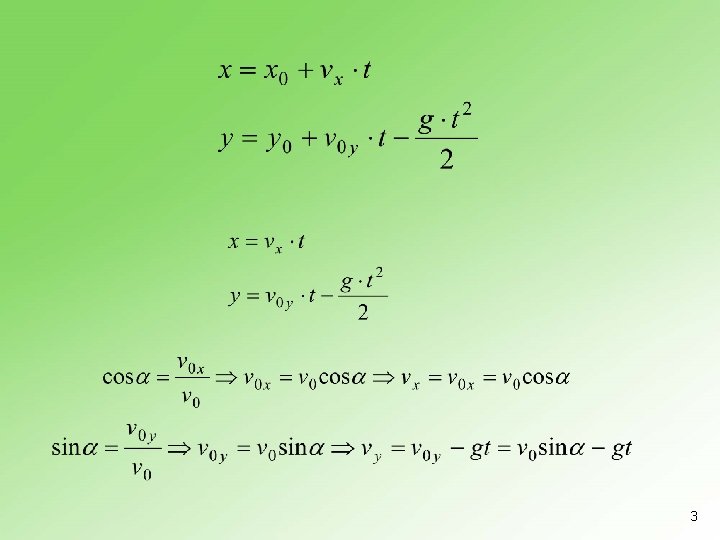
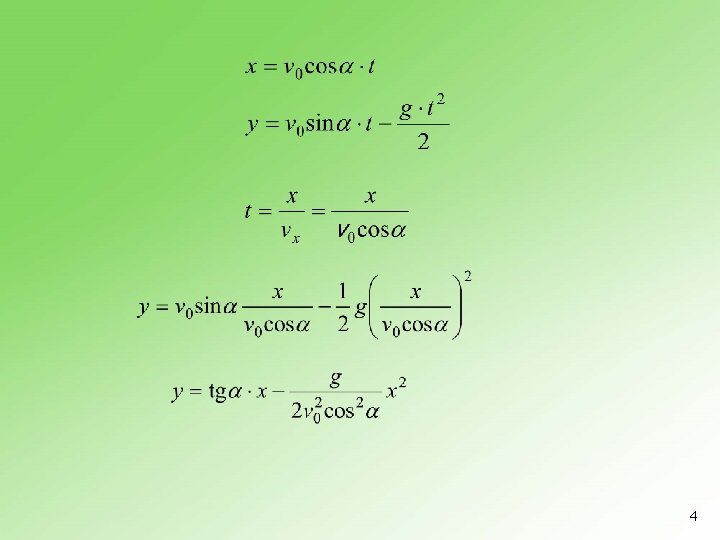

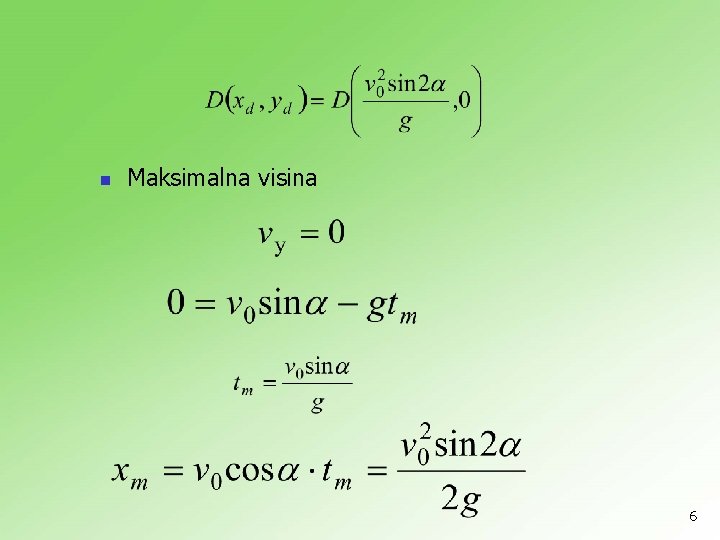
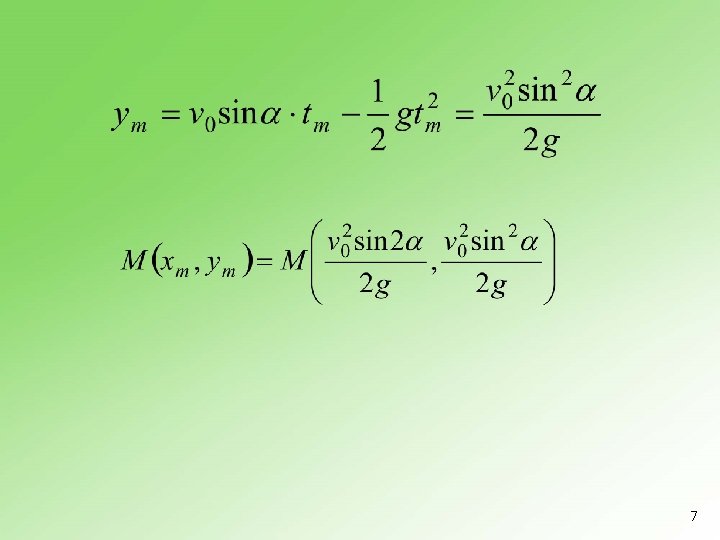

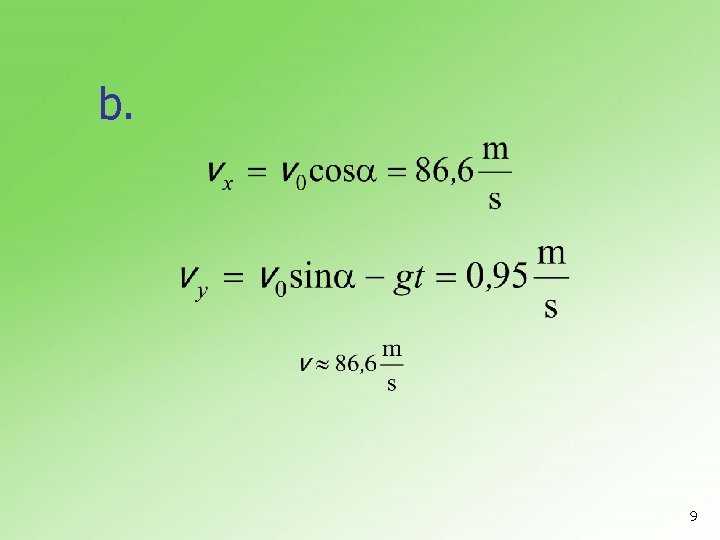
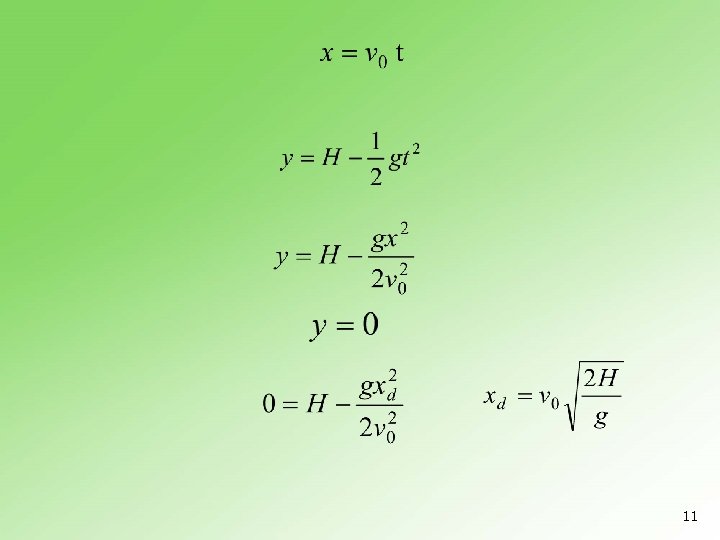
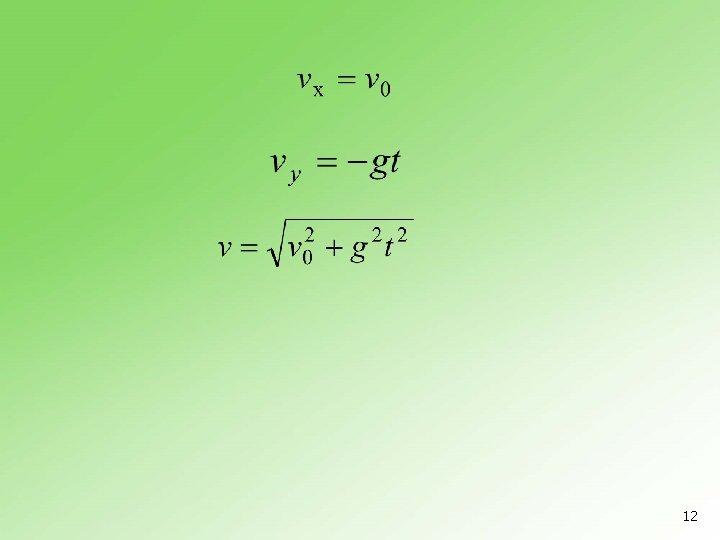

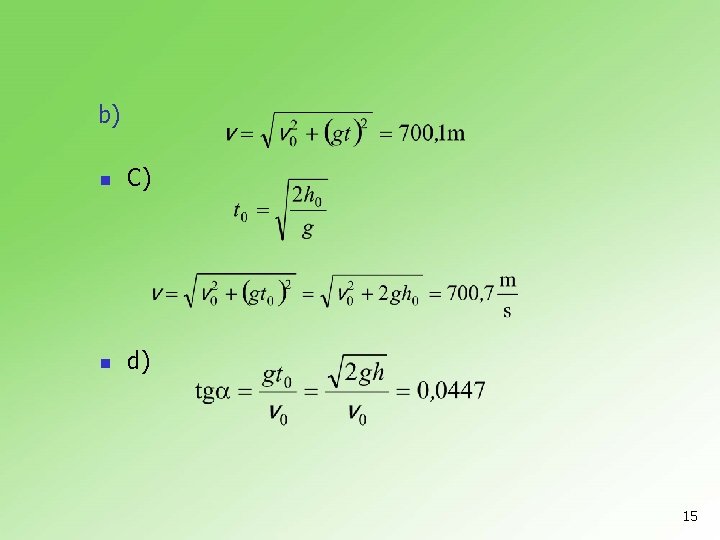
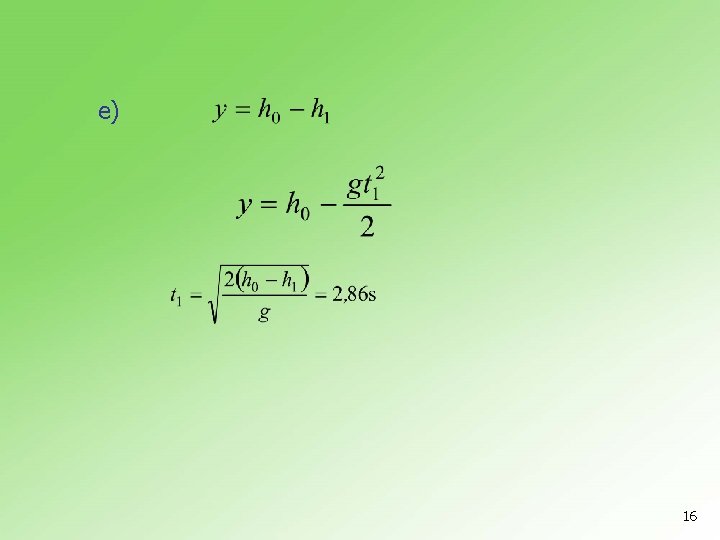


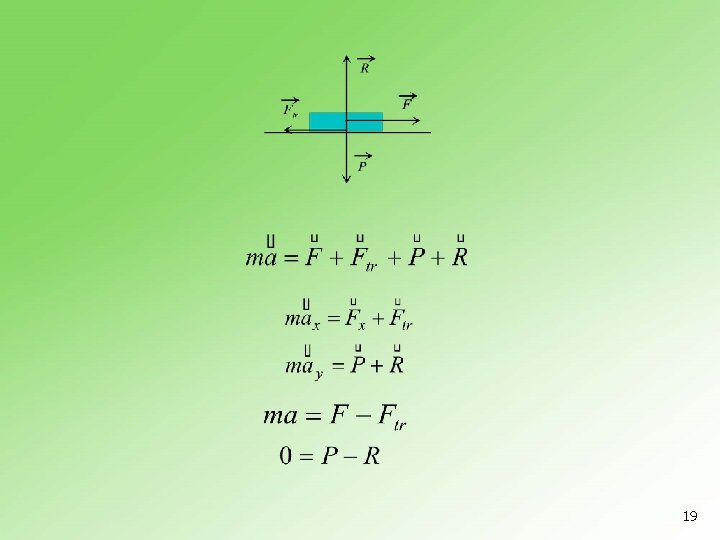
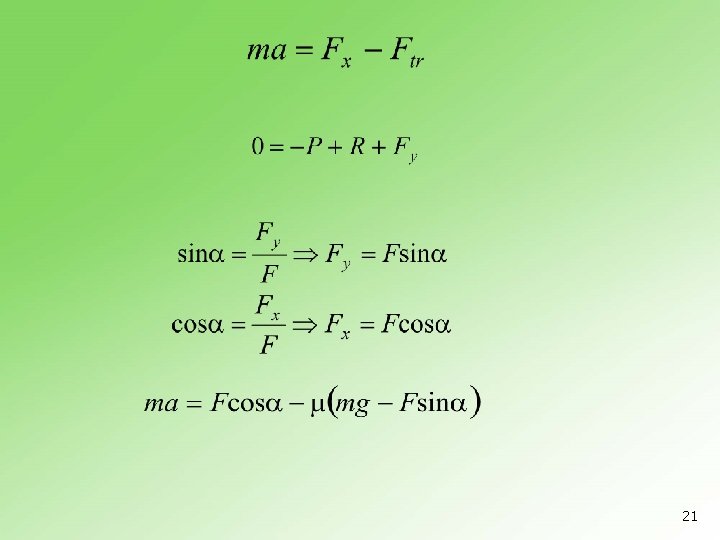



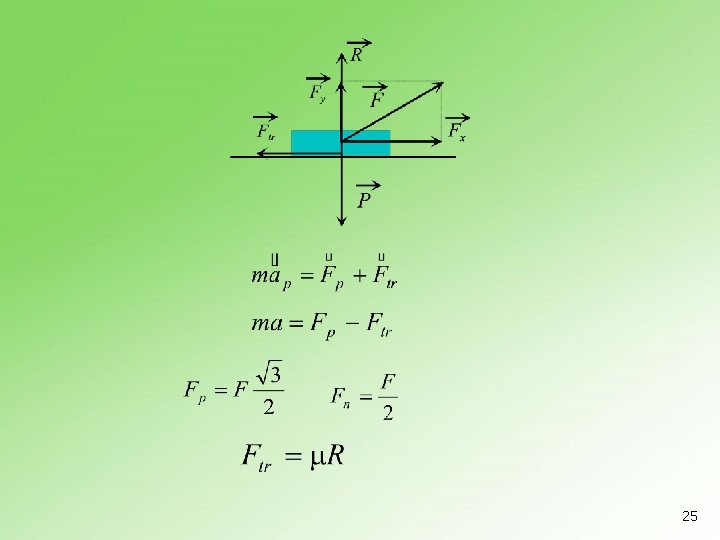
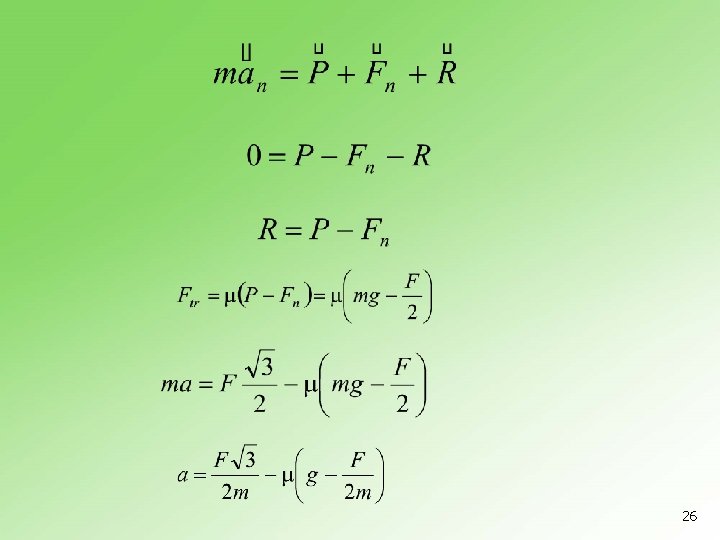


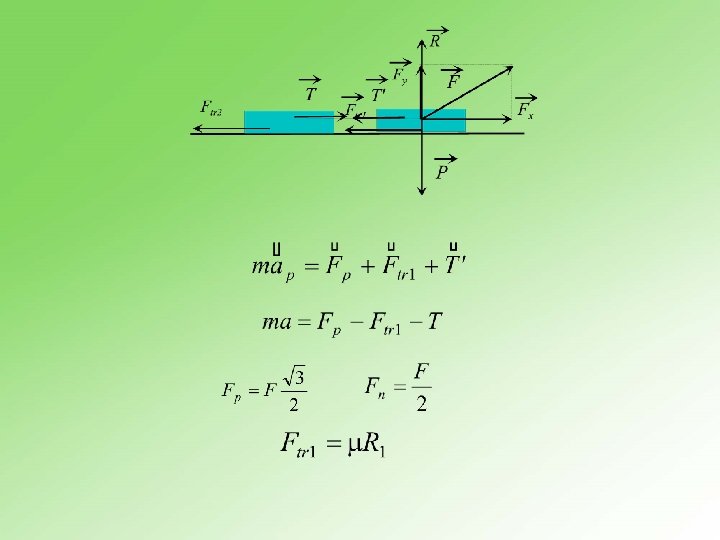
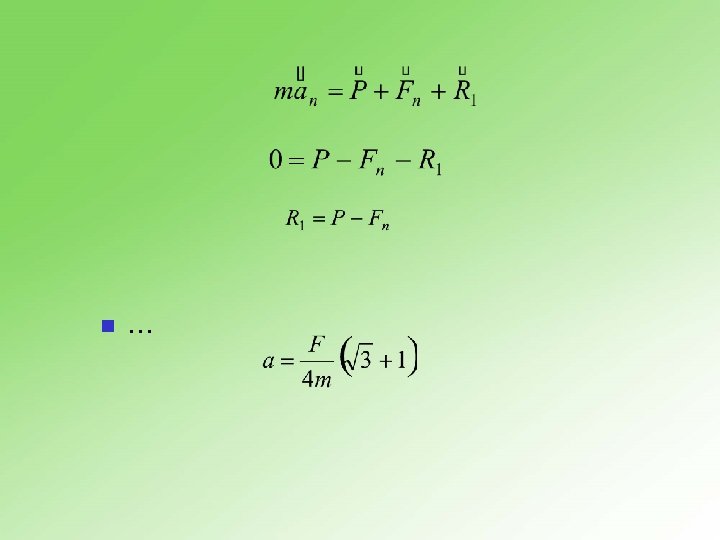

















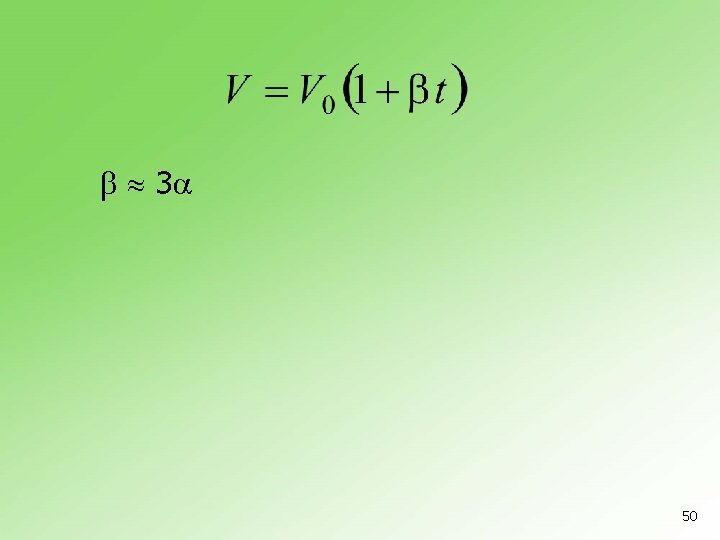


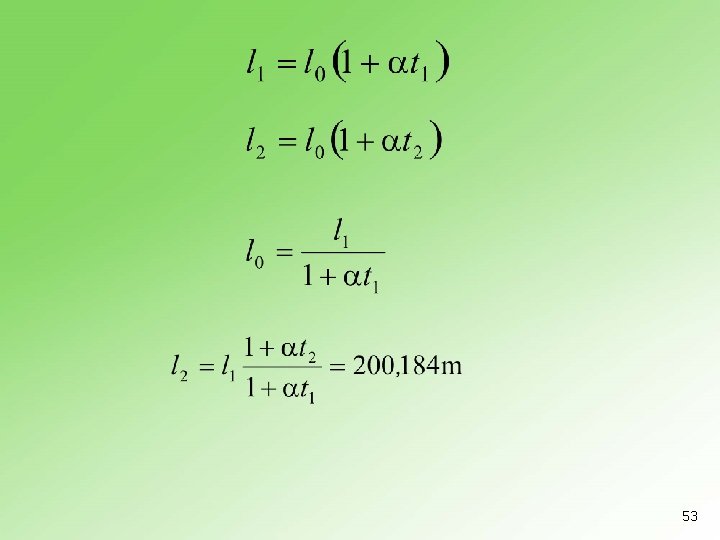

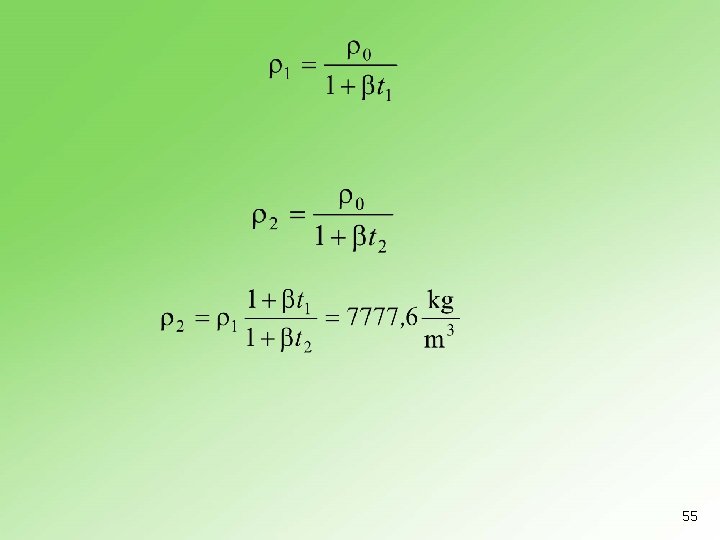

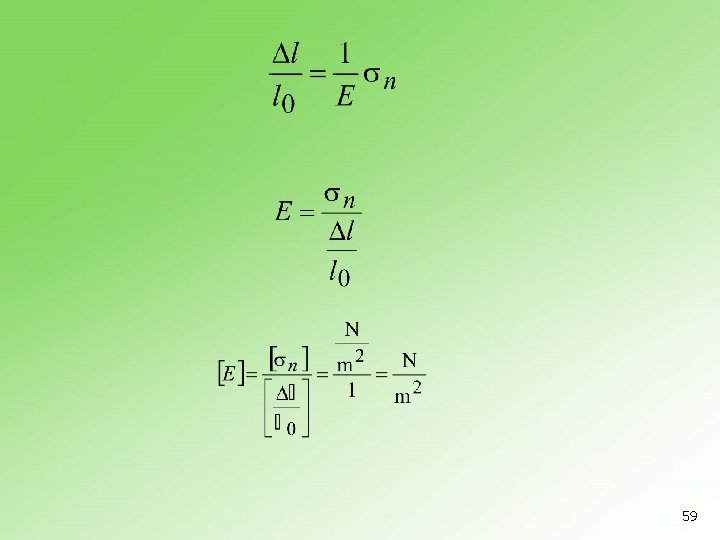


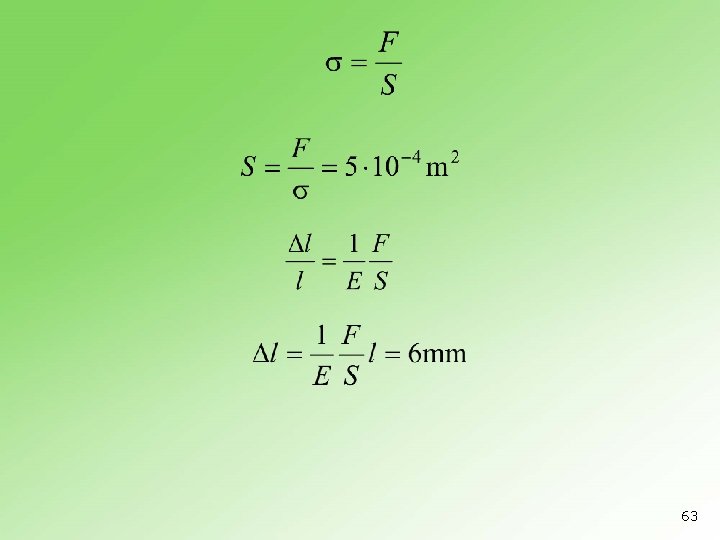
- Slides: 63

5. 7 Kosi hitac 1

2
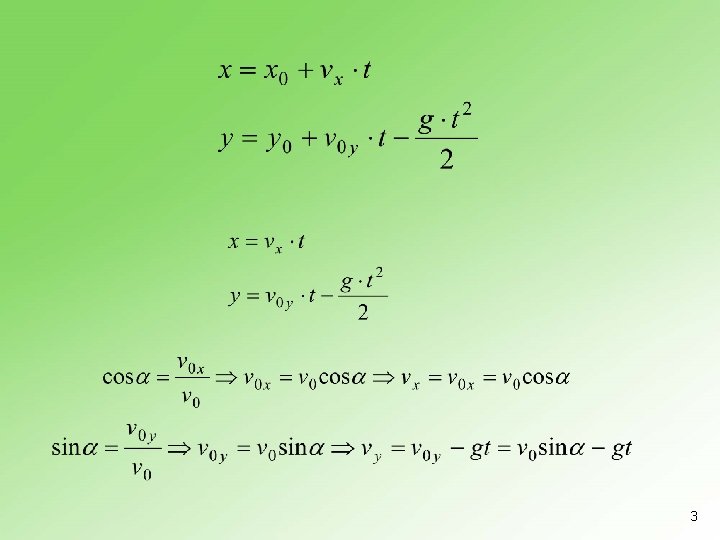
3
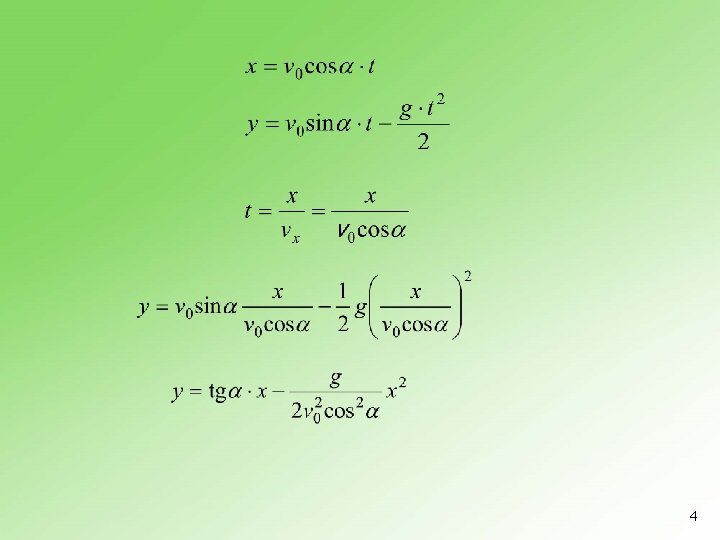
4

domet 5
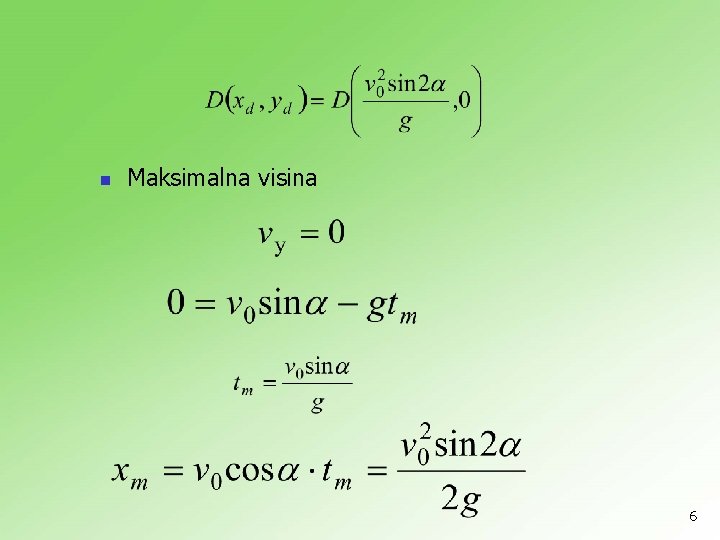
n Maksimalna visina 6
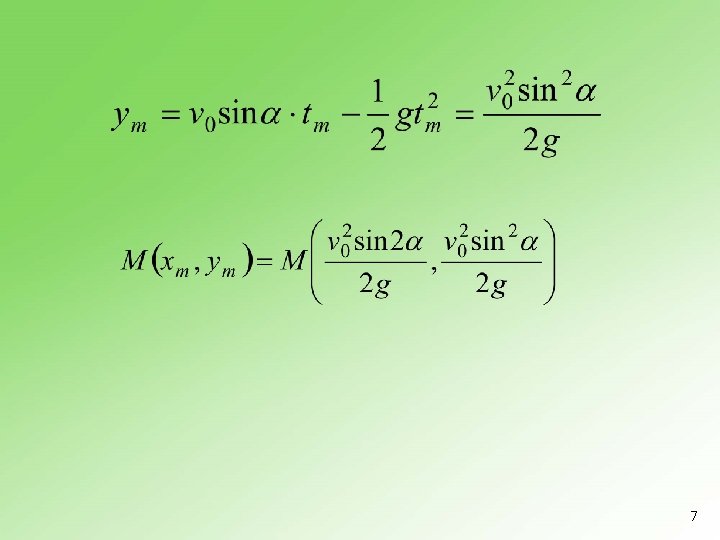
7

Telo se izbaci početnom brzinom v=100 m/s pod uglom 30 prema horizontu. a. U kom položaju će se telo nalaziti posle vremena t=5 s? b. Kolika je brzina tela u tom trenutku? n a. 8
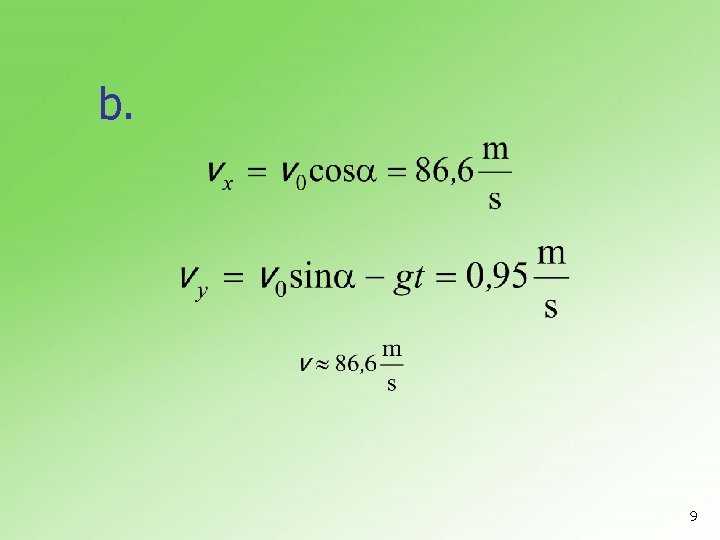
b. 9

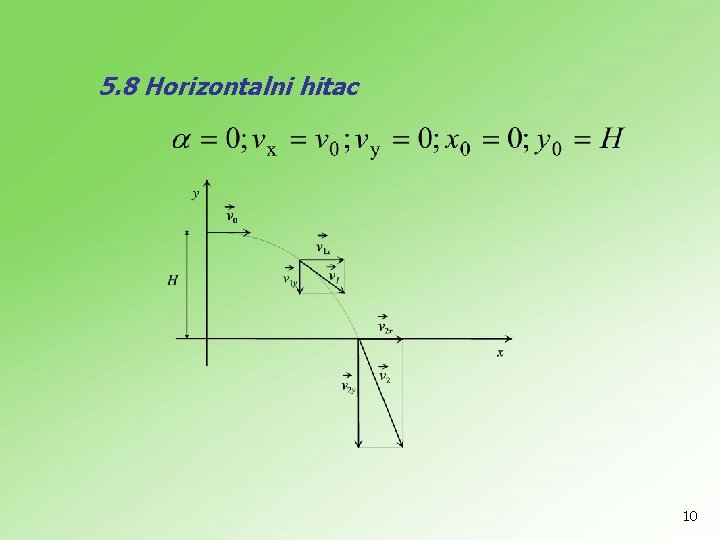
5. 8 Horizontalni hitac 10
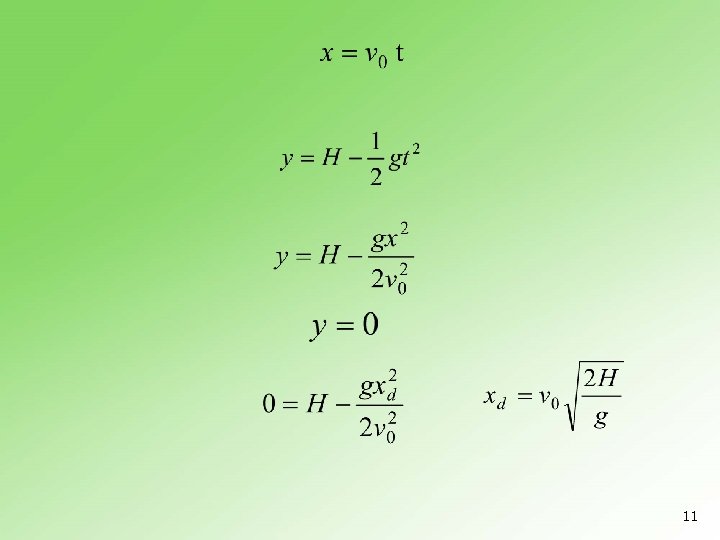
11
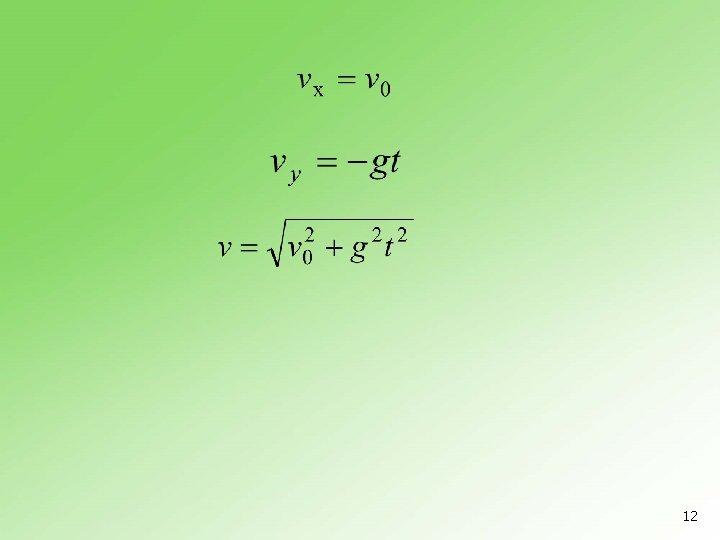
12

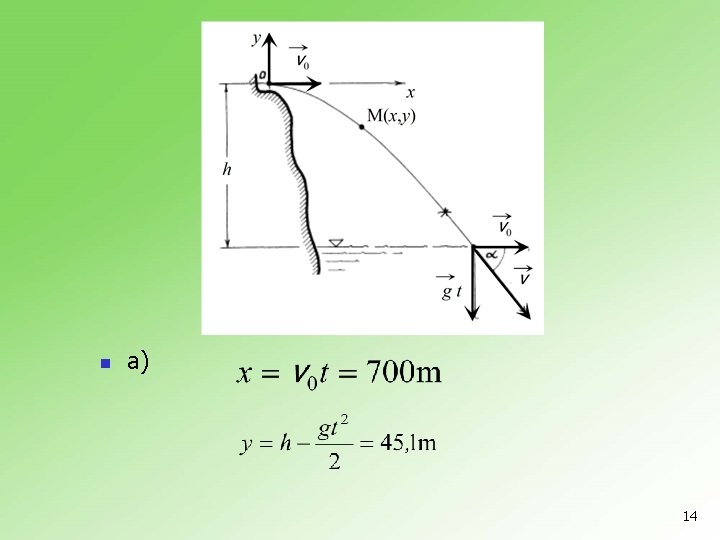
5. 8. 1 Sa morske obale, visine h 0=50 m, iz topa se ispali granata u horizontalnom pravcu. Brzina granate po ispaljenju je v 0=700 m/s. a) U kom položaju se nalazi granata posle vremena t=l s od trenutka ispaljenja? b) Kolika je brzina granate u tom trenutku? c) Kolika je brzina granate pri padu na vodu? d) Pod kojim uglom granata padne na vodu? e) Koliko treba da bude vreme tempiranja granate da bi eksplodirela na visini h 1=10 m iznad površine vode? 13

n a) 14
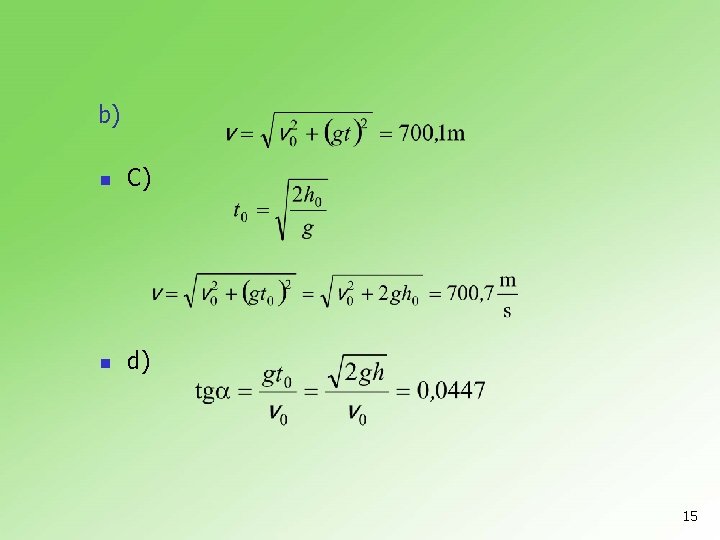
b) n C) n d) 15
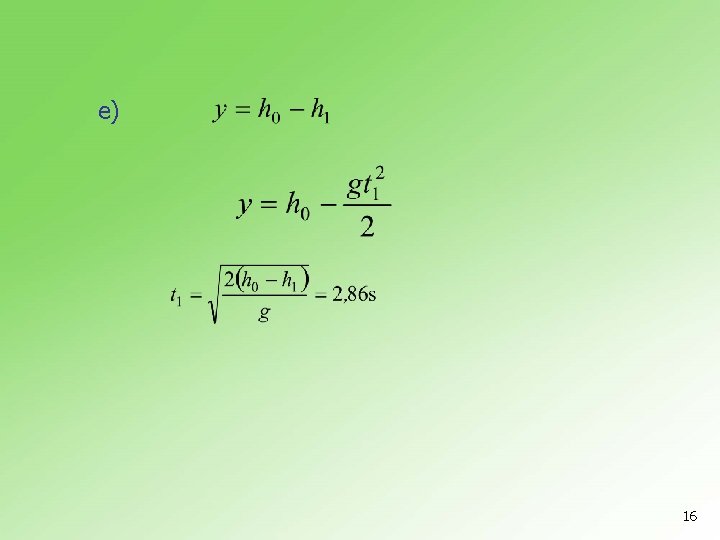
e) 16

5. 9 Trenje n n n unutrašnje i spoljašnje trenje Pod spoljašnjim trenjem se podrazumeva trenje koje se javlja između površina dva različita tela. Unutrašnje trenje se javlja između površina jednog istog tela (između slojeva tečnosti pri njihovom laminarnom kretanju, i kod gasova). Koeficijent trenja R sila reakcije podloge 17

Sile trenja postoje i kada tela miruju. 18
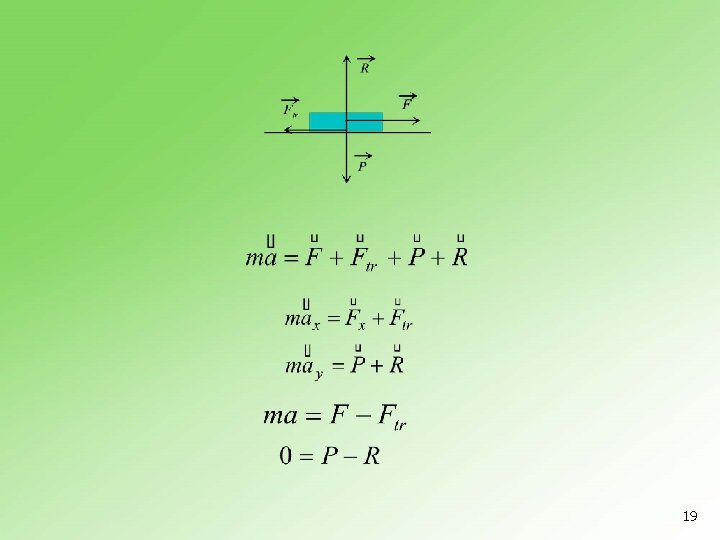
19

20
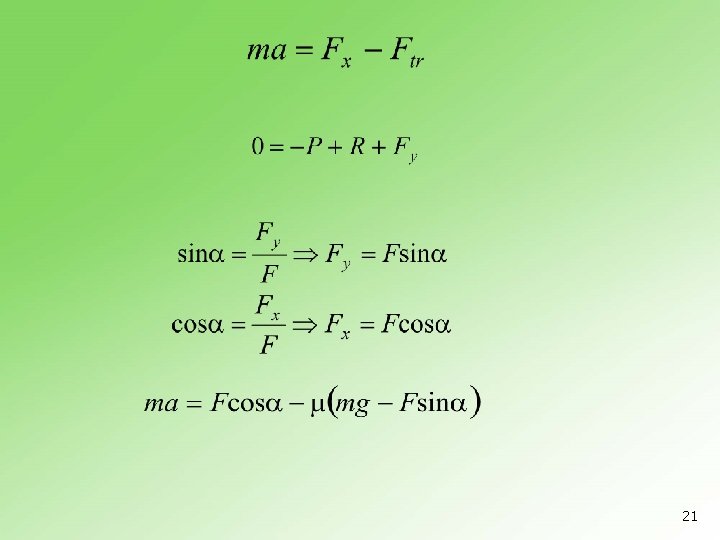
21

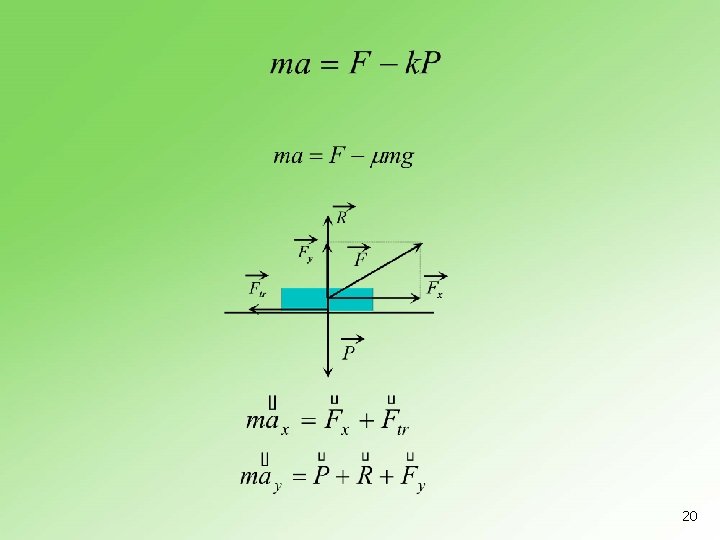
Primeri n 5. 9. 1 Telo mase m = 400 kg leži na horizontalnoj podlozi. Na telo deluje u horizontalnom pravcu sila intenziteta F = 294 N. Koliko je ubrzanje tela? Koeficijent trenja između tela i podloge iznosi = 0. 1. 22

n 5. 9. 2 Telo mase m nalazi se na horizontalnoj podlozi. Koeficijent trenja između tela i podloge je μ. Kolikom silom treba delovati na telo u horizontalnom pravcu da bi ono imalo ubrzanje jednako ubrzanju Zemljine teže? 23

n 5. 9. 3 Telo mase 3 kg leži na horizontalnoj podlozi. Na njega počne da deluje sila intenziteta 20 N pod uglom 30 prema horizontali naviše. Kolikim ubrzanjem će se kretati telo ako je koeficijent trenja 0, 4? 24
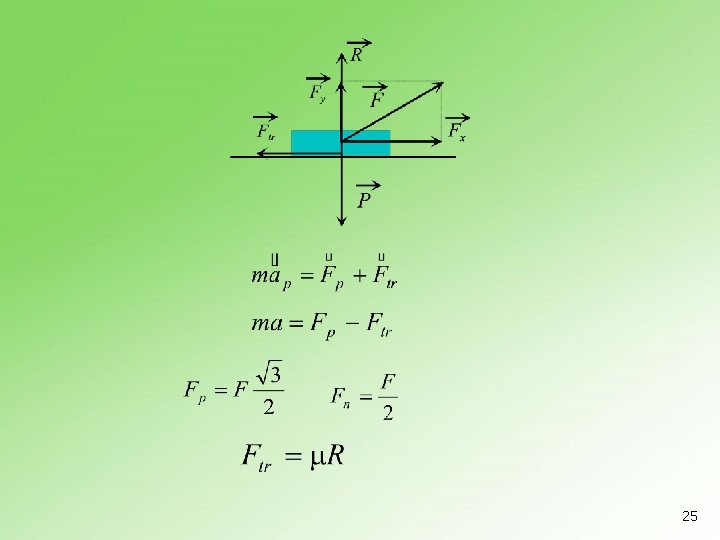
25
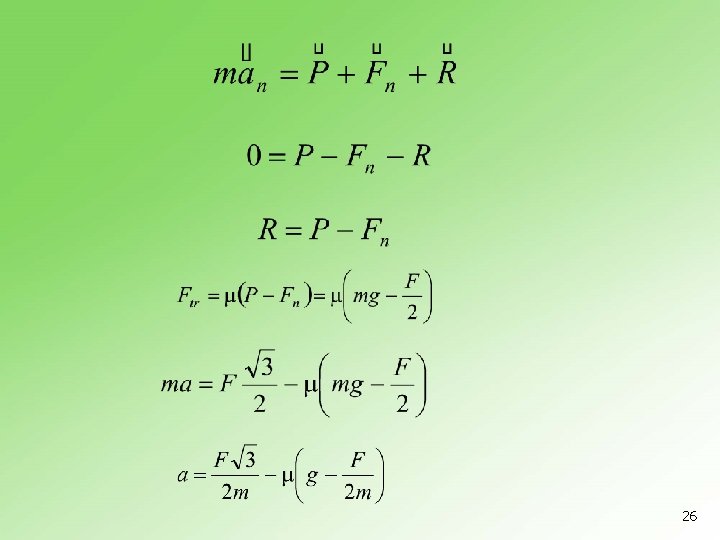
26

Domaći n 5. 9. 4 Telo mase 3 kg leži na horizontalnoj podlozi. Na njega počne da deluje sila intenziteta 20 N pod uglom 30 prema horizontali naniže. Kolikim ubrzanjem će se kretati telo ako je koeficijent trenja 0, 4? 27

5. 9. 4 Kolikim ubrzanjem se kreću tela mase m pod dejstvom sile F po podlozi u sistemu prikazanom na slici ako je koeficijent trenja ? 28
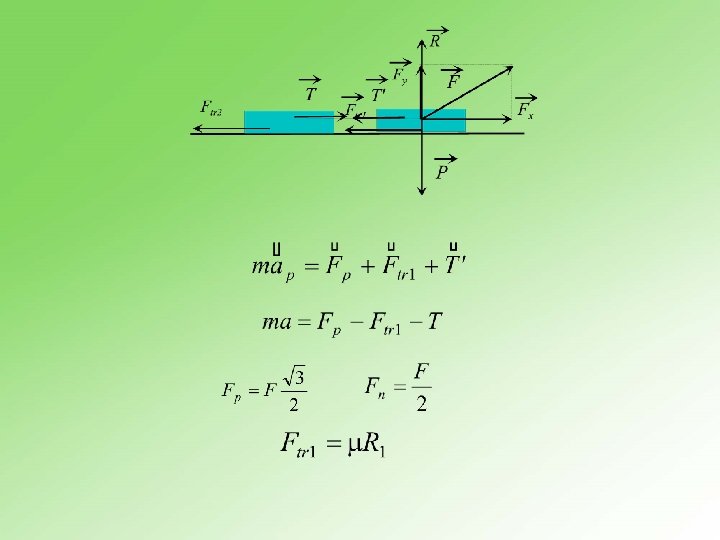
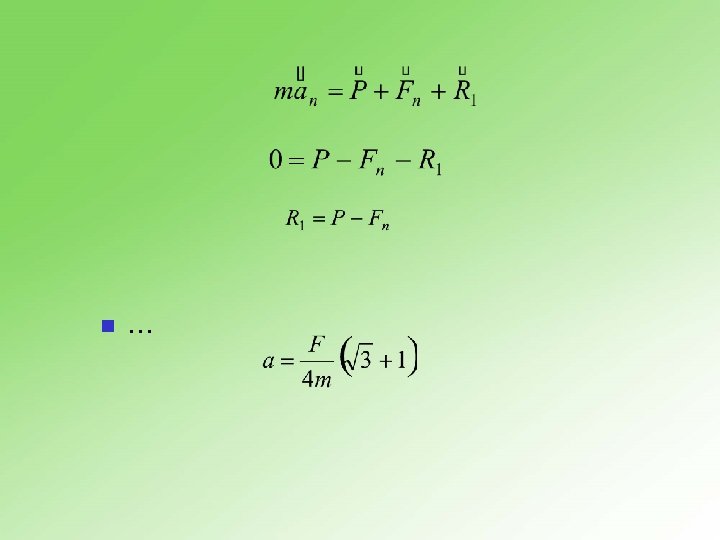

6. Struktura čvrstih tela i deformacija n n 6. 1 Struktura čvrstih tela. Kristalna rešetka Čvrsto telo se sastoji od atoma, molekula, jona i drugih elementarnih čestica, koji su na različite načine raspoređeni i međusobno povezani različitim silama. Ako su čestice raspoređene pravilno u prostoru, pri čemu se taj raspored geometrijski ponavlja, tada kažemo da telo ima kristalnu strukturu. Atomi se svrstavaju u pravilne redove i ravni i obrazuju kristalnu rešetku, pa otuda ovakva tela imaju pravilnu spoljnu geometrijsku formu, što je jedna od karakterističnih obeležja. n 31

Atom koji ulazi u sastav čvrstog tela se nalazi pod dejstvom sila koje potiču od susednih atoma. Ove sile se mećusobno kompenzuju, i atomi se nalaze u ravnoteži. Ovakav raspored atoma odgovara minimumu potencijalne energije, što daje čvrstinu kristalu u celini. n Ako atomi u čvrstom telu poseduju određen ravnotežni položaj, ali nemaju osobinu periodičnosti, za takva tela kažemo da su amorfna. Znači, amorfna tela imaju određen oblik i zapreminu, ali nemaju geometrijsku periodičnu udaljenost, pa zbog toga nemaju pravilnu geometrijsku formu. 32

U principu se sva čvrsta tela dele na kristalna i amorfna tela. n n n Osnovna karakteristika kristalnih tela je anizotropija. Ona se manifestuje u posedovanju različitih fizičkih osobina u različitim pravcima. Kristalna tela imaju različite magnetne osobine u raznim pravcima, a takođe i njihove mehaničke, toplotne, svetlosne i električne osobine zavise od pravca u kome se posmatraju. Kod kristala u određenim pravcima postoje orijentisane ravni po kojima se mnogi od njih lako cepaju. Na primer kristali kamene soli se cepaju duž uzajamno normalnih ravni, liskun na tanke listove itd. 33

Amorfna tela se mogu okarakterisati izotropijom. Pod izotropnim telima se podrazumevaju tela koja imaju iste fizičke osobine u svim pravcima, tj. njihove fizičke osobine u jednom telu su nezavisne od pravca duž koga se mere. Kao primer amorfnih tela se mogu navesti smola, vosak, staklo, plastične mase i dr. Dešava se da jedan isti materijal može da bude i u kristalnom i u amorfnom stanju, što zavisi od njegove prethodne termičke obrade. n Još jedna od bitnih karakteristika, po kojoj se razlikuju kristalna i amorfna tela je i definisanost njihove tačke topljenja. 34

n Proučavanjem kristalne strukture bavi se kristalografija, koja čini posebnu oblast u fizici čvrstog stanja. Do sada je utvrđeno da kristali poseduju različite vidove simetrije i da postoje ukupno 230 kombinacija pojedinih elemenata simetrije, koje se nazivaju prostornim grupama. Ove prostorne grupe su svrstane u 32 klase simetrije. Pošto u kristalnom telu postoji periodičnost i ponavljanje strukture, ceo kristal može biti izgrađen putem slaganja u tri različita pravca jednog istog strukturnog elementa, koji se naziva elementarna ćelija kristala. 35

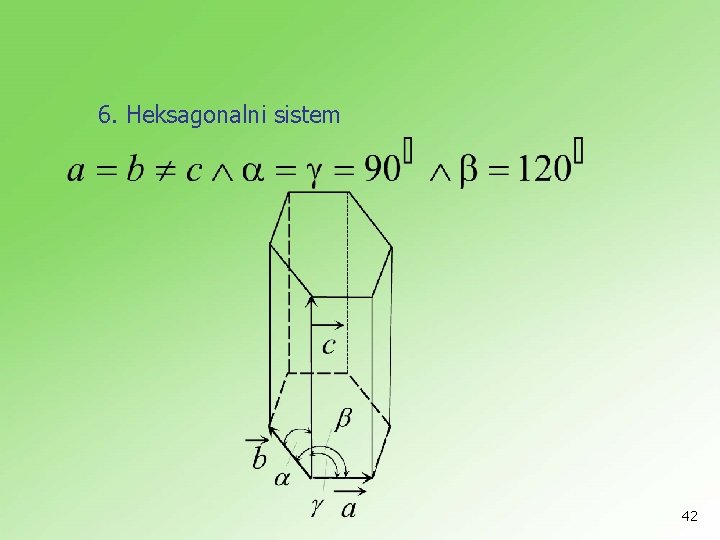
Dužine ivica takve ćelije nazivaju se periodi identičnosti a, b i c Pored ivica, paralelopiped je okarakterisan i uglovima , i , koji se nazivaju parametrima elementarne ćelije. Ako su oni poznati, onda je poznata i elementarna ćelija. Poznavanjem elementarne ćelije određena je kristalna rešetka. Ovih šest veličina nazivaju se parametri kristalne rešetke. 36

1. Triklinički sistem 37

2. Monoklinički sistem 38

3. Rombički sistem 39

4. Tetragonalni sistem 40

5. Romboedarski (trigonalni) sistem 41

6. Heksagonalni sistem 42

7. Kubni sistem 43

6. 2 Fizički tipovi kristalnih rešetki n n Jonski kristali Kod ovih kristala u čvorovima kristalne rešetke naizmenično su raspoređeni pozitivni i negativni joni. Joni su između sebe povezani električnim silama kulonovskog tipa. Hemijska veza, koja nastaje usled delovanja ovih sila, naziva se jonska veza. Tipičan primer jonske veze je kristal natrijum hlorida (Na. Cl). Jonski kristali se rastvaraju u vodi obrazujući pozitivne i negativne jone. Temperatura topljenja ovih kristala je relativno visoka, a imaju i veliku tvrdoću. 44

Atomski kristali n n U čvorovima ovog tipa kristala se nalaze neutralni atomi. Atomi su međusobno povezani kovalentnim vezama, koje takođe imaju električni karakter, ali nisu kulonovskog tipa. Kovalentne veze se ostvaruju preko elektronskih parova, tj. preko valentnih elektrona, pri čemu dolazi do stalne razmene ovih elektrona između atoma. Materijali, sastavljeni od ovog tipa kristala, imaju visoku temperaturu topljenja i vrlo veliku tvrdoću. Tipičan primer atomskih kristala je dijamant i grafit, koji, u stvari, predstavljaju dve alotropske modifikacije ugljenika. 45

Metalni kristali n Kod ovih kristala u čvorovima kristalne rešetke se nalaze pozitivni joni između kojih se kreću slobodni elektroni. Ovakvi elektroni u metalima se tretiraju kao "elektronski gas" i proučavaju na osnovu kinetičke teorije gasova. Broj slobodnih elektrona je približan broju valentnih elektrona u metalnom atomu. Prisustvom slobodnih elektrona u metalima objašnjavaju se njihove osobine kao što su: električna i toplotna provodljivost, metalni sjaj itd. Metalna veza je vrlo jaka, pa ovi materijali imaju visoku temperaturu topljenja i veliku tvrdoću, ali i veliku sklonost ka mehaničkoj deformaciji, koja omogućava da im se da potreban oblik pri odgovarajućoj obradi. 46

Molekulski kristali n U čvorovima prostorne rešetke nalaze se orijentisani molekuli međusobno povezani interagujućim silama Van der Valsovog tipa. Ove sile su slabe pa zato ove kristale odlikuje mala tvrdoća i niske temperature topljenja. Kristali ovog tipa se uglavnom dobijaju prevođenjem običnih gasova u kristalno stanje na niskim temperaturama (Ne, Ar, Kr, H 2, O 2 itd). Molekulsku rešetku ima većina organskih jedinjenja kao što su: parafin, naftalin i dr. 47

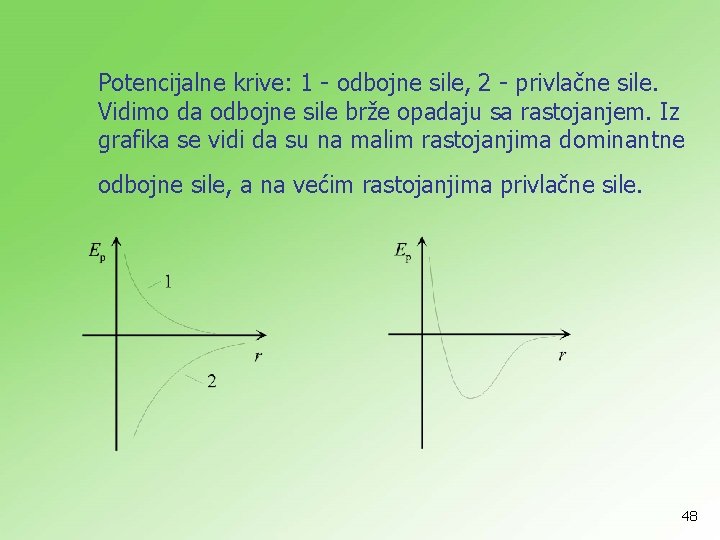
Potencijalne krive: 1 - odbojne sile, 2 - privlačne sile. Vidimo da odbojne sile brže opadaju sa rastojanjem. Iz grafika se vidi da su na malim rastojanjima dominantne odbojne sile, a na većim rastojanjima privlačne sile. 48

6. 3 Toplotno širenje čvrstih tela 49
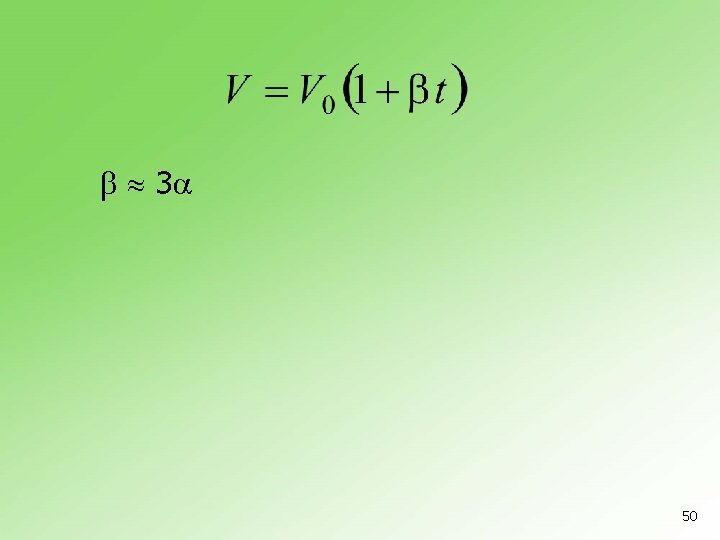
3 50

Primer Dužina šine na temperaturi 23 C iznosi 116 m. Kolika joj je dužina na 0 C? Termički koeficijent linearnog širenja iznosi 1, 2 10 -5 C-1. 51

n Dužina aluminijumske žice između dva dalekovodna stuba zimi, na -10 C, iznosi 200 m. Kolika će biti dužina iste žice leti na 30 C? Termički koeficijent linearnog širenja za aluminijum iznosi 2, 3 10 -5 C-1. 52
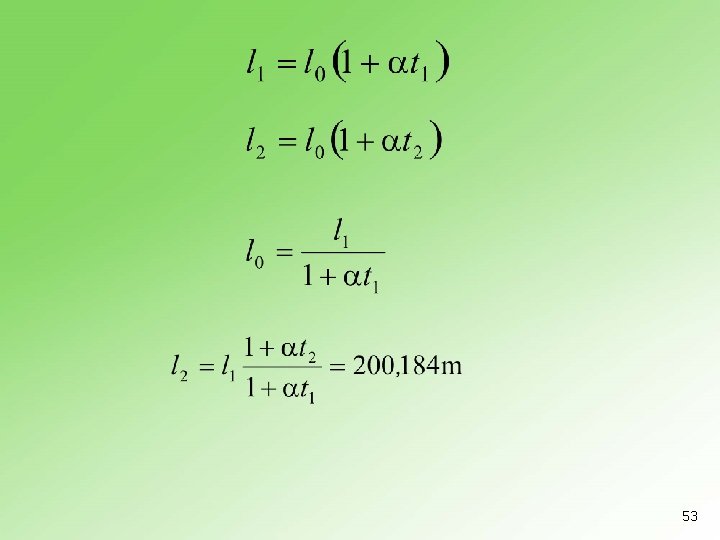
53

Gustina gvožđa na 20 C iznosi 7800 kg/m 3. Kolika mu je gustina na 100 C? Koeficijent zapreminskog širenja gvožđa iznosi 3, 6 10 -5 C-1. 54
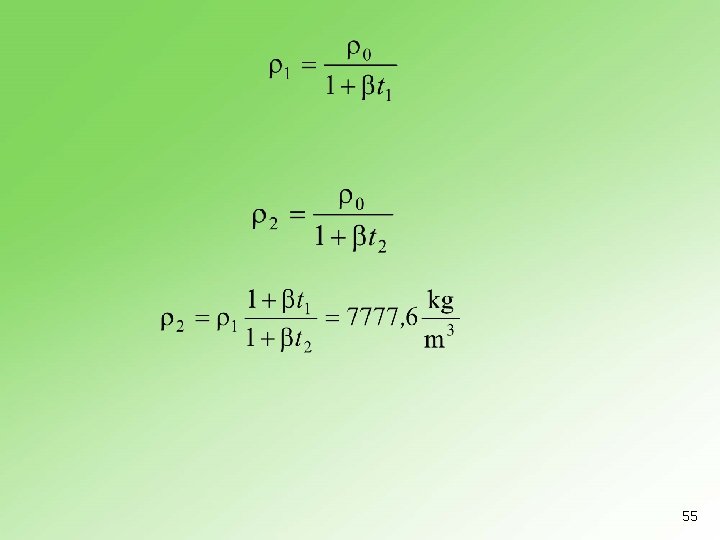
55

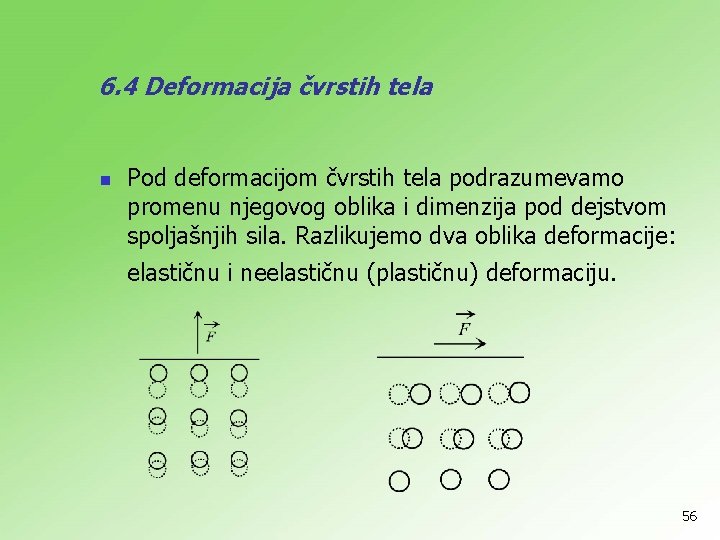
6. 4 Deformacija čvrstih tela n Pod deformacijom čvrstih tela podrazumevamo promenu njegovog oblika i dimenzija pod dejstvom spoljašnjih sila. Razlikujemo dva oblika deformacije: elastičnu i neelastičnu (plastičnu) deformaciju. 56

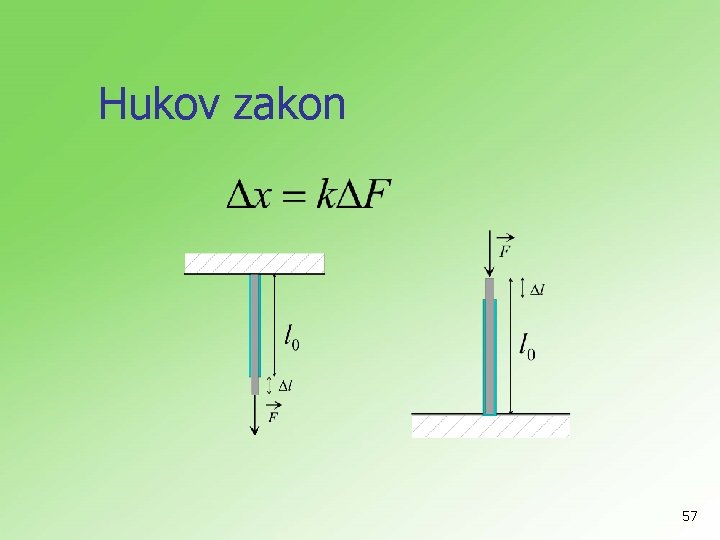
Hukov zakon 57

n - koeficijent elastičnosti koji zavisi samo od svojstava materijala n Jangov modul elastičnosti n normalni napon 58
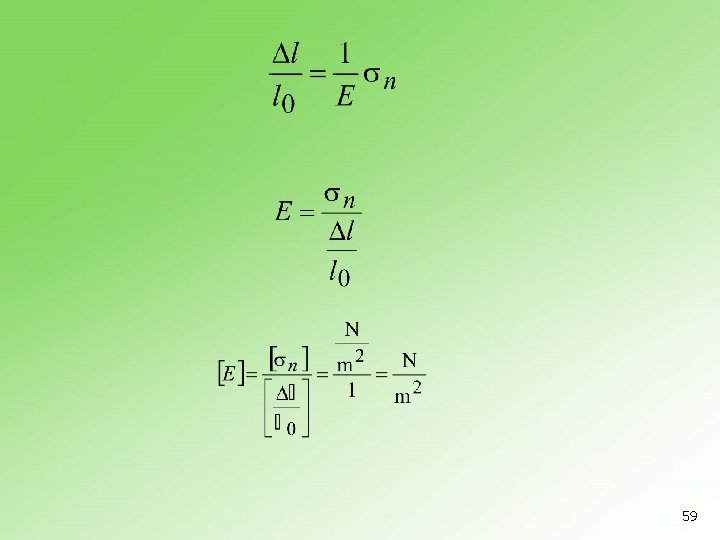
59

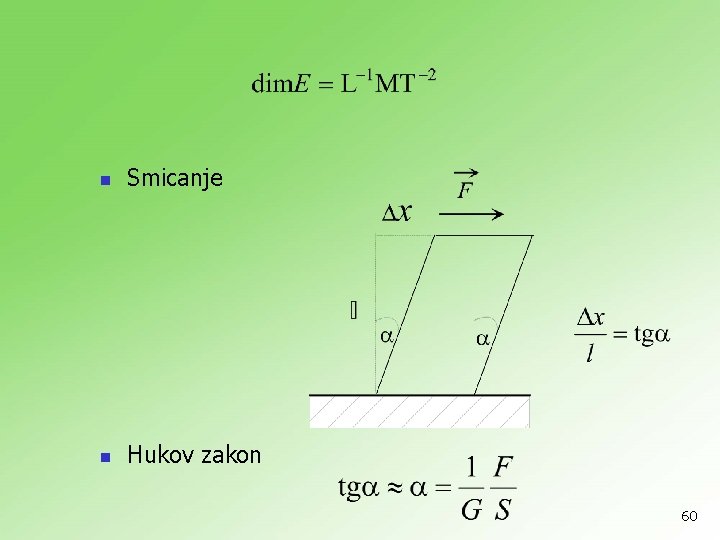
n Smicanje n Hukov zakon 60

Koliki najmanji poluprečnik žice treba uzeti da pri opterećenju od 3039, 52 N ne nastane plastična deformacija? Granica elastičnosti materijala od kojeg je žica napravljena iznosi. 61

n Kolikog poprečnog preseka treba da bude čelična šipka da bi pri opterećenju od 30 k. N napon u njoj iznosio. Naći apsolutno istezanje iste šipke ako je njena dužina 20 m, a modul elastičnosti . 62
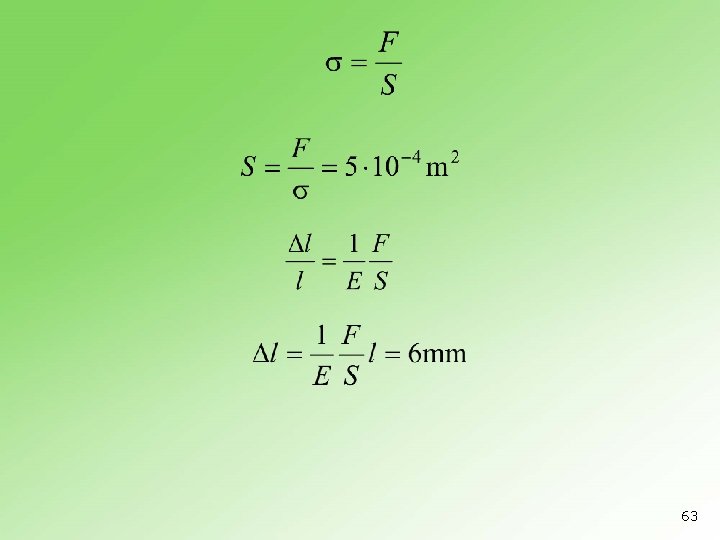
63