5 7 Complex Numbers Objectives Identify operate with

5. 7 Complex Numbers

Objectives: • Identify, operate with, and graph complex numbers. • Find the complex roots of quadratic equations that model real-world situations.

Complex Numbers • A complex number has a real part & an imaginary part. • Standard form is: Real part Example: 5+4 i Imaginary part

Example 1: Name the real part and the imaginary part of each complex number. a) 2 + 4 i Real: 2 Imaginary: 4 i b) 0 – 3 i Real: 0 Imaginary: -3 i c) 0 + 6 i Real: 0 Imaginary: 6 i d) 7 + 0 i Real: 7 Imaginary: 0 i e) -1 – 0 i Real: -1 Imaginary: 0 i

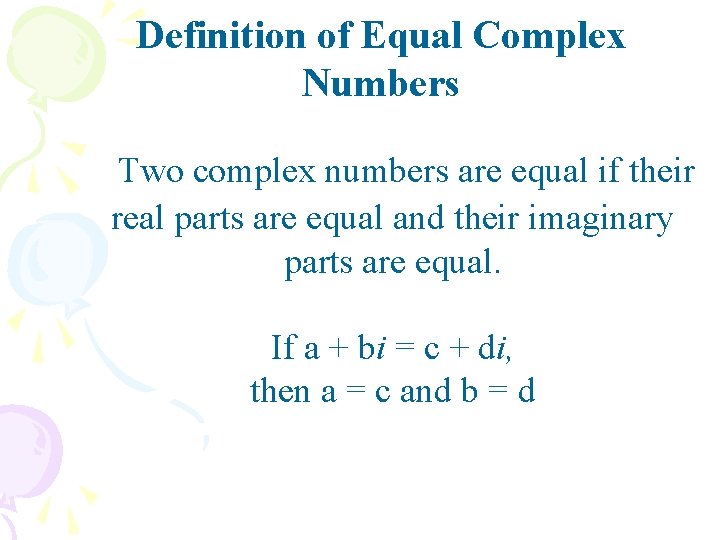
Definition of Equal Complex Numbers Two complex numbers are equal if their real parts are equal and their imaginary parts are equal. If a + bi = c + di, then a = c and b = d

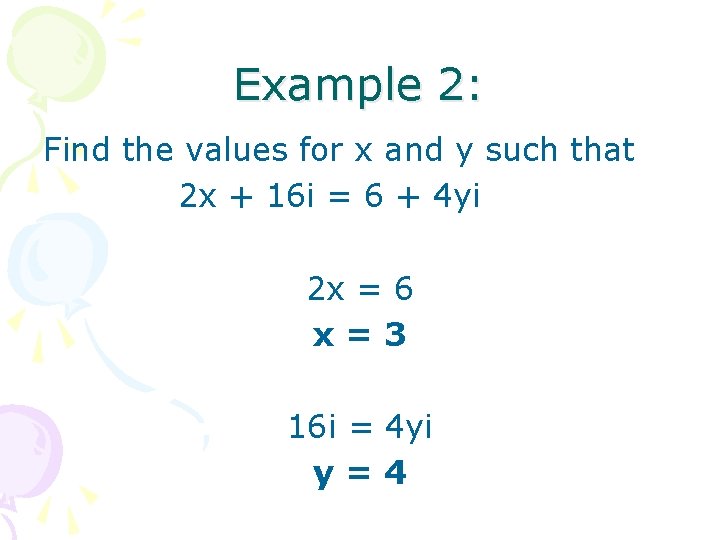
Example 2: Find the values for x and y such that 2 x + 16 i = 6 + 4 yi 2 x = 6 x=3 16 i = 4 yi y=4

Operations of Complex Numbers • Operating with complex numbers is very similar to operating with binomials. • Treat i like a variable.

When adding or subtracting complex numbers, combine like terms. Example 3: a) Simplify:

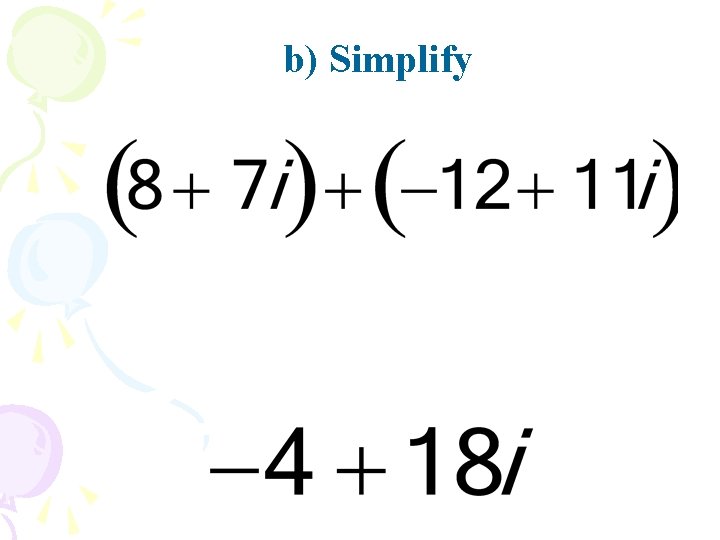
b) Simplify

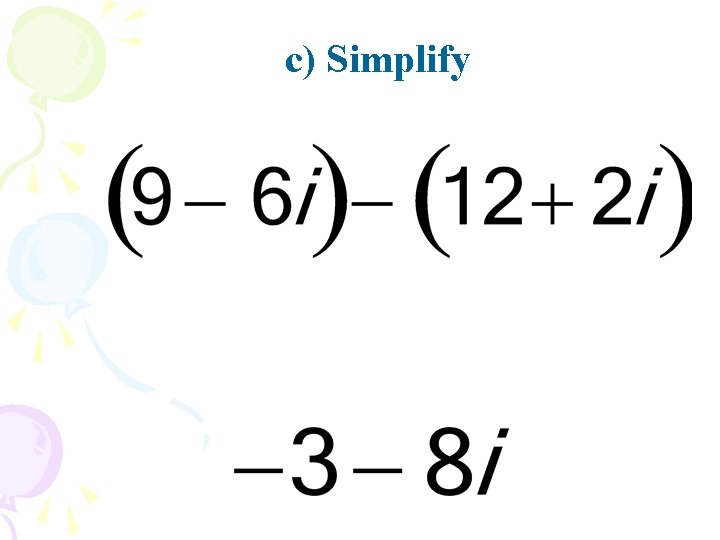
c) Simplify

Multiplying complex numbers To multiply complex numbers, you use the same procedure as multiplying binomials.

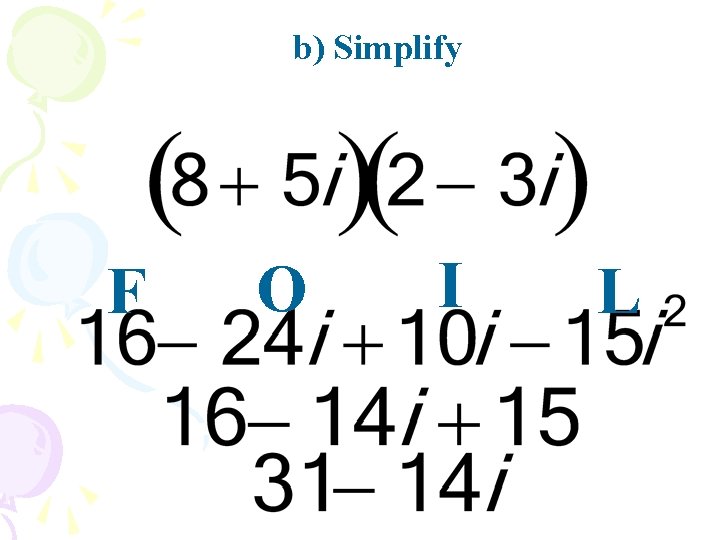
b) Simplify F O I L

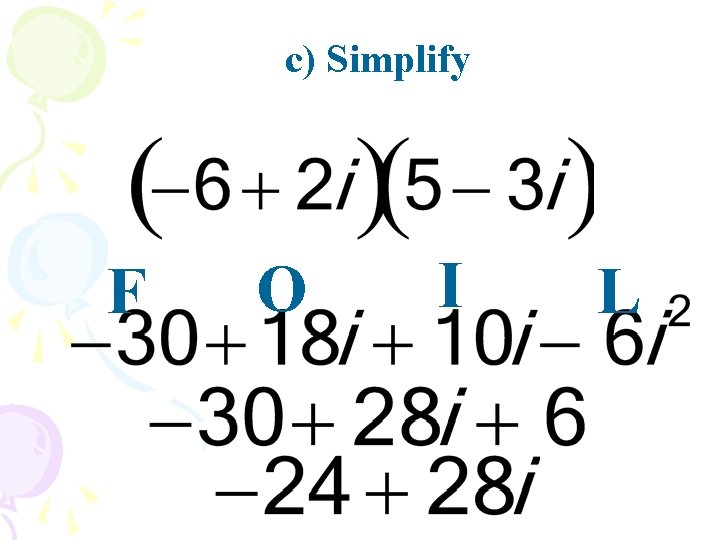
c) Simplify F O I L

How do we handle quadratic equations with complex roots? Example 5: Do Now: Solve the following quadratic: x 2 – 8 x + 17 = 0

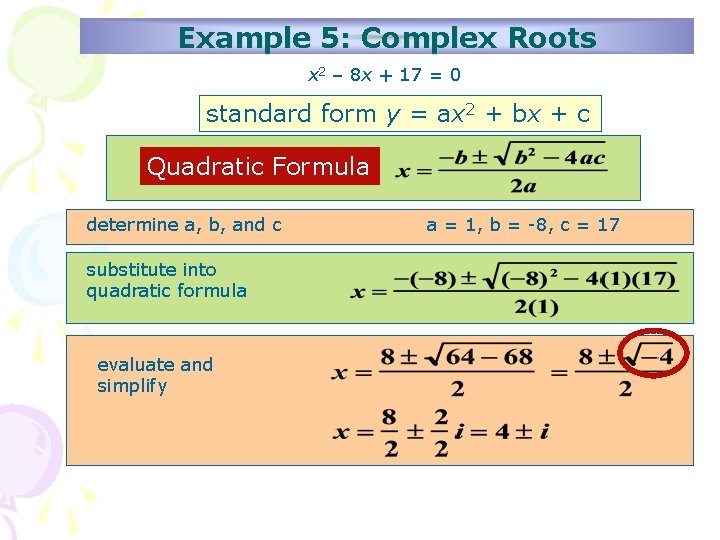
Example 5: Complex Roots x 2 – 8 x + 17 = 0 standard form y = ax 2 + bx + c Quadratic Formula determine a, b, and c substitute into quadratic formula evaluate and simplify a = 1, b = -8, c = 17

Example 6: Solve the equation and express its roots in the form a + bi. put in standard form determine a, b, and c substitute into quadratic formula evaluate and simplify x 2 – 2 x + 10 = 0 a = 1, b = -2, c = 10

Classwork: Operations with Complex Numbers Worksheet

Homework Pg 299 -300 Exercises: 1 -4, 7 -15, 18 -21

Example 7: A manufacturing company is selling a new product and they want to know if it would be profitable to do so. The variable x represents the number (in hundreds) of items manufactured and sold. The cost is C(x) = 3 x + 40 The revenue is R(x) = -x² + 15 x a) Find the break even points, where the cost equals the revenue. Use your graphing calculator to check your answer. b) Should the company launch their new product? Explain.

• Example 7: The solutions are not real, so there are no break even points. On the graph, they do NOT intersect.

Example 7: b) Should the company launch their new product? Explain. The cost function is always above the revenue function. Therefore, cost always exceeds revenue. They should NOT launch their new product.

Conjugates In order to simplify a fractional complex number, use a conjugate. What is a conjugate?

Example 8: Simplify a) Use the conjugate

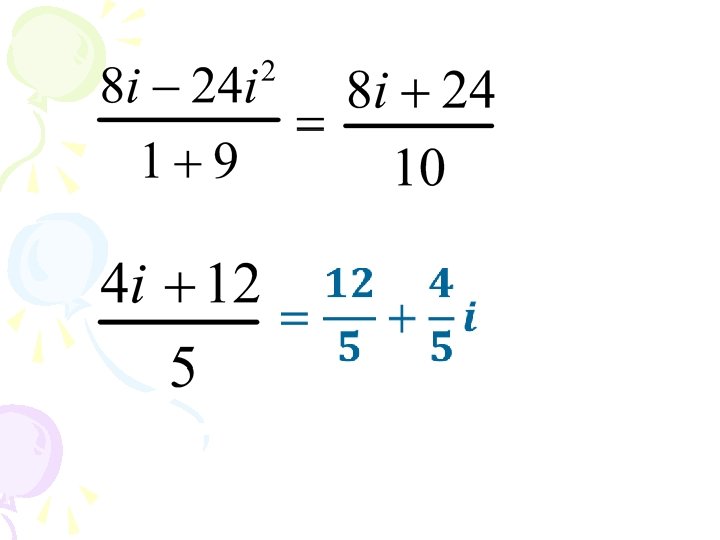
Example 8 (Continued) You try these! b) c)

The Complex plane Real Axis Imaginary Axis

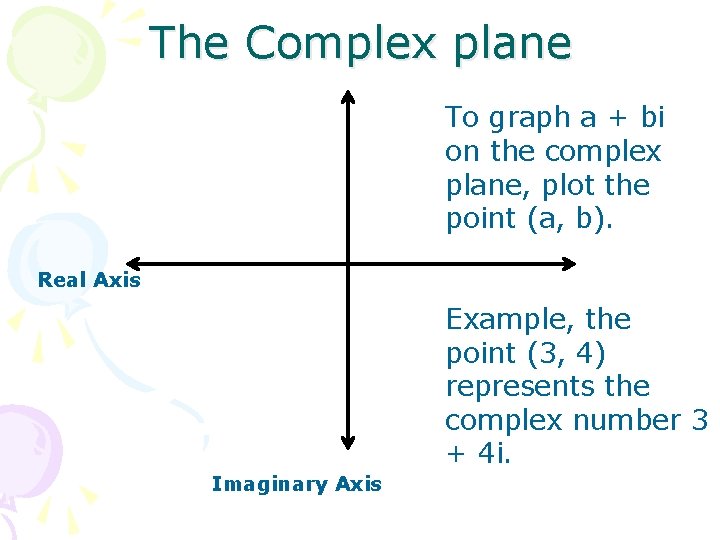
The Complex plane To graph a + bi on the complex plane, plot the point (a, b). Real Axis Example, the point (3, 4) represents the complex number 3 + 4 i. Imaginary Axis

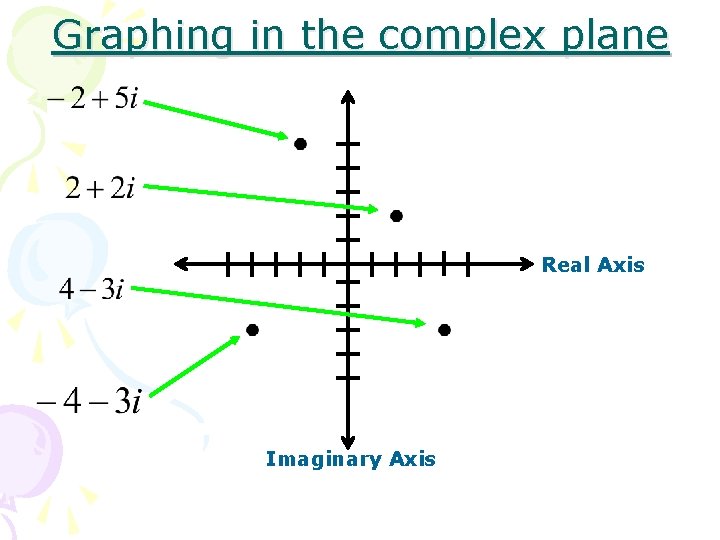
Graphing in the complex plane Real Axis Imaginary Axis

Homework: 5. 7 Practice and Apply