5 6 Solving Logarithmic and Exponential Equations Exponentials

5. 6 - Solving Logarithmic and Exponential Equations Exponentials: ex: ln(ex) = x… ex + 5 = 60 4 e 2 x = 5 so if ex = 2… ex = 55 e 2 x = 5/4 ln(ex) = ln(2) ln(ex) = ln(55) ln(e 2 x) = ln(5/4) x = ln(2) x = ln(55) 2 x = ln(5/4) / 2

ex: e 2 x (ex 3 ex - 2) +2=0 (ex - 1) = 0 ex: Other Bases 2 x = 10 ln(2 x) = ln(10) (ex - 2) = 0 (ex - 1) = 0 ex = 2 ex = 1 ln(ex) = ln(2) ln(ex) = ln(1) x = ln(2) = 0. 693 x=0 x ln(2) = ln(10) x = ln(10) / ln(2) = 3. 322

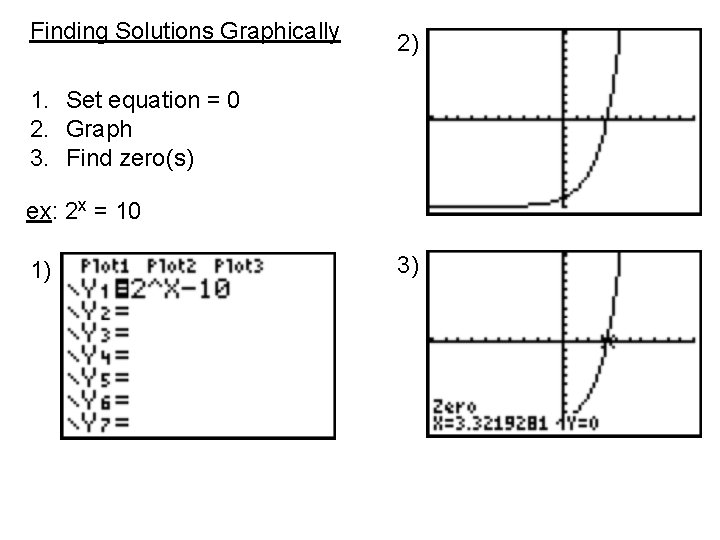
Finding Solutions Graphically 2) 1. Set equation = 0 2. Graph 3. Find zero(s) ex: 2 x = 10 1) 3)

IC 5. 6 A - pg 386 #’s 1, 2, 4, 5, 8, 10, 11, 14, 15, 18, 19, 22, 25, 26, 30, 31, 34.

Solving Logarithmic Equations • Exponentials and logs are inverse functions • So for logs we raise both sides of the equation up as exponents…the base of the exponential we are creating is the base of the log statement (e for ln’s / whatever ‘a’ is for logs) • We call this ‘exponentiation’ • ex: 2 ln 3 x = 4 5 + 2 ln x = 4 ln x = 3 eln x = e 3 2 ln x = -1 ln 3 x = 2 x = e 3 ln x = -1/2 e(ln 3 x) = e 2 eln x = e(-1/2) 3 x = e 2 x = e(-1/2) x = e 2/3

Other Bases ex: log 4 x = 3 5 + 2 log 3 x = 4 2 log 23 x = 4 4(log 4 x) = 43 2 log 3 x = -1 log 23 x = 2 x = 43 = 64 log 3 x = -1/2 2(log 23 x) = 22 3(log 3 x)= 3(-1/2) 3 x = 4 x = 3(-1/2) x = 4/3

Shortcut ex: log 10(x + 2) = log 10 (3 x - 4) Drop log statements (x + 2) = (3 x - 4) 2 x = 6 x=3 Multiple log (or ln) statements ln(x - 3) + ln(2 x + 1) = 2(ln x) Combine with laws of logs ln[(x – 3)(2 x + 1)] = ln x 2 Drop log statements (x – 3)(2 x + 1) = x 2 2 x 2 - 5 x – 3 = 0 Factor / Graph

Creating log (or ln) statements from constants loga ax = x so… log 10 10 = 1 log 10 102 = 2 log 10 103 = 3 etc… ln e = 1 ln e 2 = 2 ln e 3 = 3 ex: 2 + ln (x + 4) = ln 16 ln e 2 (x + 4) = ln 16 Combine log statements e 2 (x + 4) = 16 Drop log statements x = (16/e 2) - 4

IC 5. 6 B – pg 386 #’s 37, 38, 41, 42, 4548 all, 52.