5 5 The Substitution Rule revisited What happens

5. 5 The Substitution Rule revisited! What happens if you need to integrate something that doesn’t fit a rule?

When trying to figure out a “u(x)” function, I generally look at where the integrand is busy and has stuff in it I don’t know what to do with. 1. Pick a u(x). Figure out du. If du is also there (or mostly there, except for a constant multiple, you are successful. 2. Sometimes you can anticipate the extra constant needed and not have to do an explicit substitution.

Other times, to keep it all straight, you have to do an explicit substitution and maybe even change to different forms of u combined with x to replace all needed. Evaluate the indefinite integral.

When doing definite integrals, remember you HAVE to show the integration by hand. To get EXACT answers, sometimes you have to evaluate by hand as well. That means you have 2 choices. 1. Integrate by hand, making u-substitutions when necessary. If plugging in values for the limits a and b, you must make sure you switch back to the beginning variable to evaluate. 2. Or. . . If you make a u-substitution, you can actually switch the whole problem over to “u” things by switching the limits of integration over as well. The evaluation is MUCH easier to do.

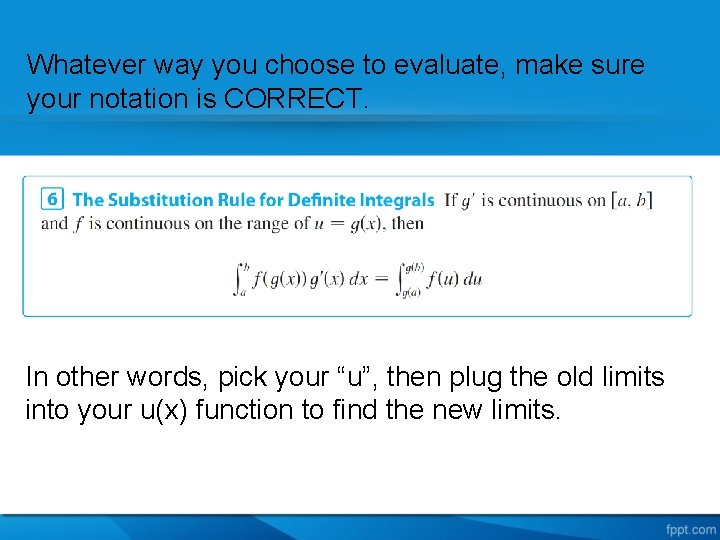
Whatever way you choose to evaluate, make sure your notation is CORRECT. In other words, pick your “u”, then plug the old limits into your u(x) function to find the new limits.

Evaluate the definite integral.

As you can see, it is much harder to integrate than derive. Evaluating definite integrals are an added amount of work. So whenever possible, we want our work to be made easier. That can happen when we notice symmetry.