5 5 Solving Polynomial Equations Part 1 1

1 8 27 64 125 216 343 512 729 1000 Perfect Cubes

• A. Factor the polynomial x 3 – 729. If the polynomial cannot

• Pull out the GCF! Examples: Factor the expression. • 1. 64 h

• B. Factor the polynomial 24 x 5 + 3 x 2 y

• Method used to factor polynomials with 4+ terms - Must be even

• A. Factor the polynomial 2 2 3 a + 3 ay +

• B. Factor the polynomial x 3 + 5 x 2 – 4

• 1. Factor the polynomial d 3 + 2 d 2 + 4

• 2. Factor the polynomial 64 x 9 + 27 y 5. If

• 3. Factor the polynomial r 3 + 4 r 2 – 9

• 4. Factor the polynomial 54 x 5 + 128 x 2 y

Algebra 2 5. 5 Day 2 Solving Polynomial Equations

It is like factoring a quadratic – just not second degree. Quadratic Form Examples:

Examples: 3. 25 x 4 – 36 Quadratic Form 4. 4 x 6 –

1. 2. 3. 4. Put the polynomials in standard form Factor as far as

Slides: 24

Download presentation

5. 5 Solving Polynomial Equations Part 1 1

Factoring Patterns 2

1 8 27 64 125 216 343 512 729 1000 Perfect Cubes

• A. Factor the polynomial x 3 – 729. If the polynomial cannot be factored, write prime. 4

• Pull out the GCF! Examples: Factor the expression. • 1. 64 h 4 – 27 h • 2. x 3 y + 343 y What’s the first thing we do when we factor?

• B. Factor the polynomial 24 x 5 + 3 x 2 y 3. If the polynomial cannot be factored, write prime. 6

• Method used to factor polynomials with 4+ terms - Must be even number of terms • Group 1 st half of terms & 2 nd half of terms and find GCF’s - After taking GCF’s, remaining polynomials should be identical • Re-write separate factors - You may have to factor multiple times after factoring by grouping. Factoring by Grouping 7

3 x 3 – 36 x 2 + 2 x – 24 4 x 2 y 2 – 16 y 2 – 9 x 4 + 36 x 2 Factor by Grouping 8

• A. Factor the polynomial 2 2 3 a + 3 ay + 2 ay + 6 y. If the polynomial cannot be factored, write prime. 10

• B. Factor the polynomial x 3 + 5 x 2 – 4 x – 20. If the polynomial cannot be factored, write prime. 11

• 1. Factor the polynomial d 3 + 2 d 2 + 4 d + 8. If the polynomial cannot be factored, write prime. You try! 12

• 2. Factor the polynomial 64 x 9 + 27 y 5. If the polynomial cannot be factored, write prime. You try! 13

• 3. Factor the polynomial r 3 + 4 r 2 – 9 r – 36. If the polynomial cannot be factored, write prime. You try! 14

• 4. Factor the polynomial 54 x 5 + 128 x 2 y 3. If the polynomial cannot be factored, write prime. You try! 15

Algebra 2 5. 5 Day 2 Solving Polynomial Equations

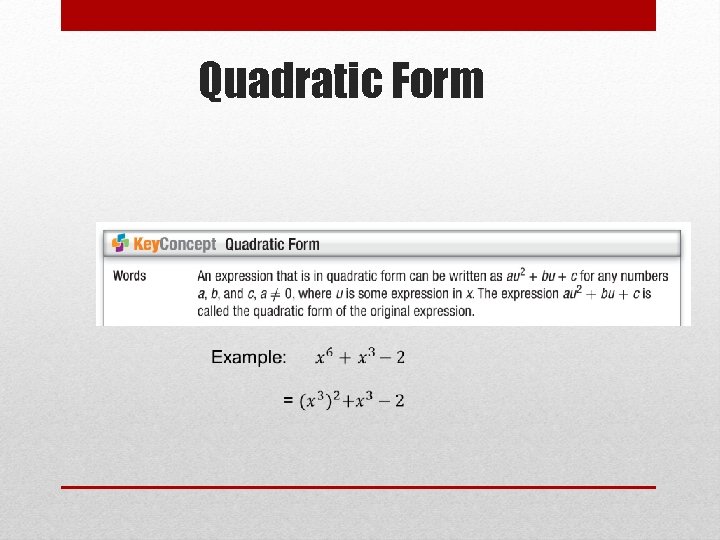
Quadratic Form

It is like factoring a quadratic – just not second degree. Quadratic Form Examples: 1. x 4 + 10 x 2 + 16 2. x 4 – 6 x 2 – 27

Examples: 3. 25 x 4 – 36 Quadratic Form 4. 4 x 6 – 20 x 4 + 24 x 2

1. 2. 3. 4. Put the polynomials in standard form Factor as far as you can – starting with the GCF – be careful Set all the factors with variables equal to zero Solve these new equations Solve polynomials by factoring

2 + 2 x = 0 1. x Examples: Solve.

3 – 2 = 0 Solve. 2. 54 x. Examples:

3. 3 x 3 + 7 x 2 = 12 x Solve. 4. x 3– 18 = - 2 x 2 + 9 x

5. x 4 – 29 x 2 + 100 = 0 Solve.