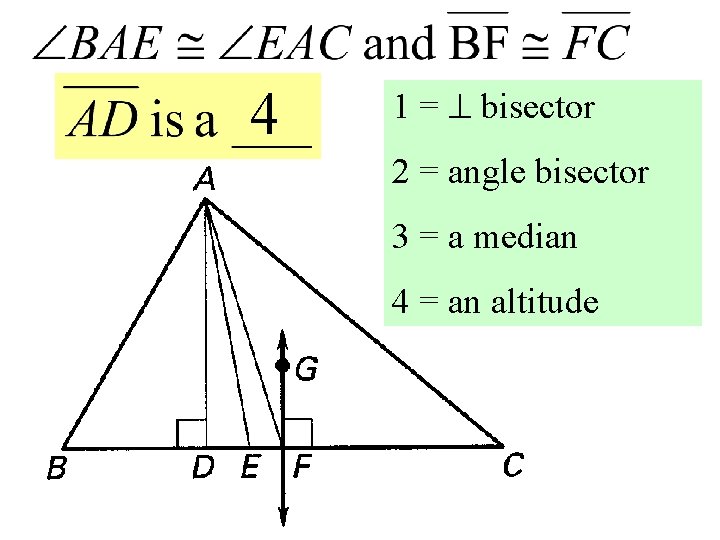
5 4 Use Medians and Altitudes Median of

5. 4 Use Medians and Altitudes

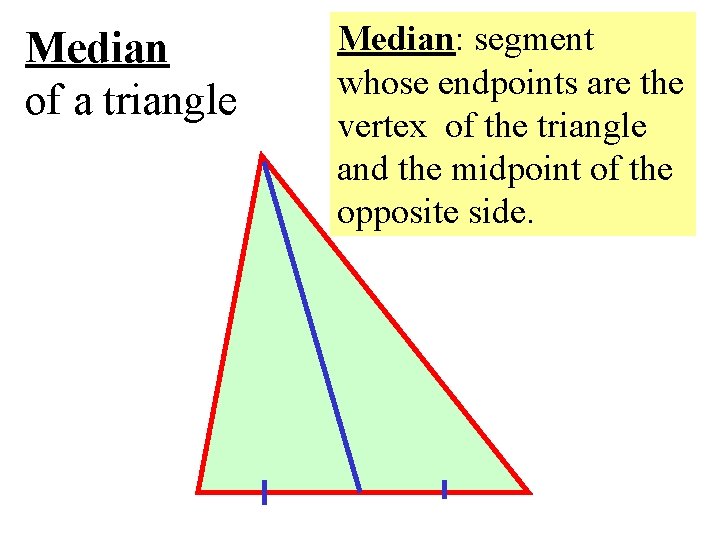
Median of a triangle Median: segment whose endpoints are the vertex of the triangle and the midpoint of the opposite side.

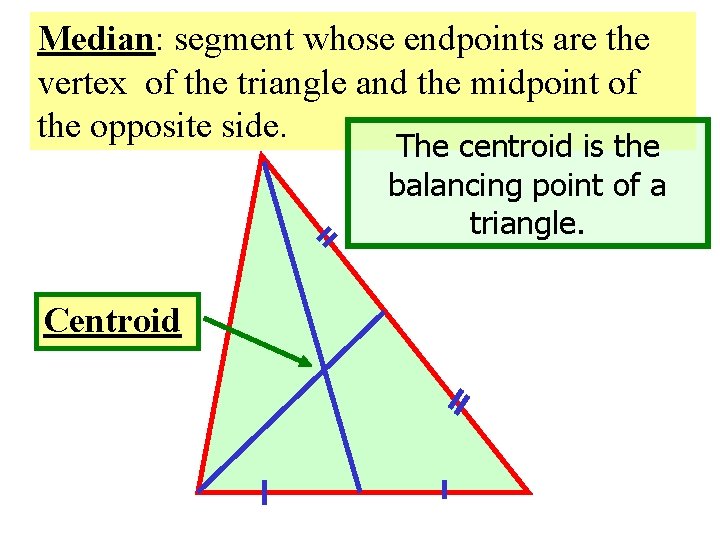
Median: segment whose endpoints are the vertex of the triangle and the midpoint of the opposite side. The centroid is the balancing point of a triangle. Centroid

Theorem 5. 8 Concurrency of Medians The medians of a triangle intersect at a point that is two thirds of the distance from each vertex to the midpoint of the opposite side. A W B X D Y C

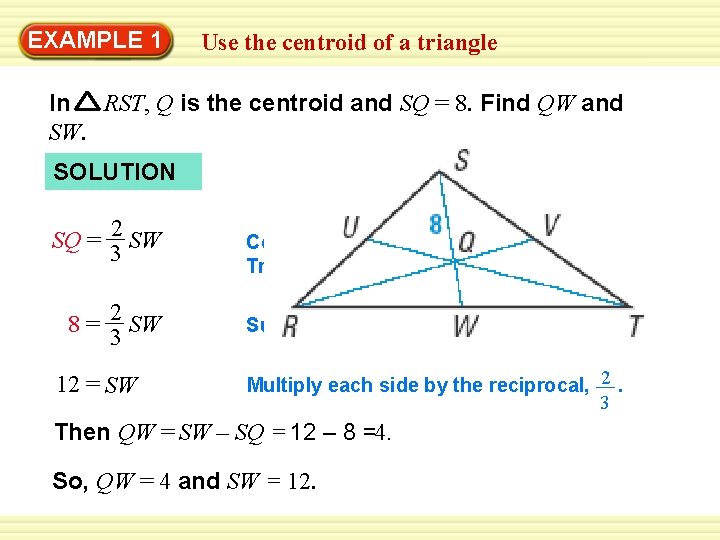
EXAMPLE 1 Use the centroid of a triangle In RST, Q is the centroid and SQ = 8. Find QW and SW. SOLUTION SQ = 2 SW 3 8 = 2 SW 3 12 = SW Concurrency of Medians of a Triangle Theorem Substitute 8 for SQ. Multiply each side by the reciprocal, 2. 3 Then QW = SW – SQ = 12 – 8 =4. So, QW = 4 and SW = 12.

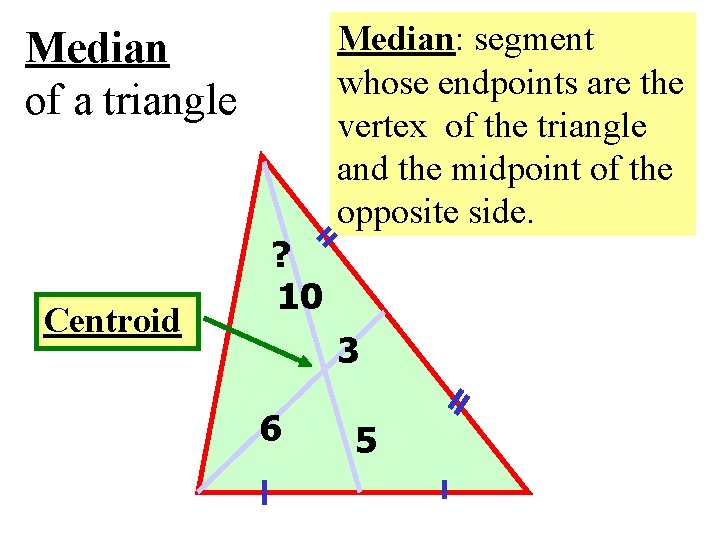
Median: segment whose endpoints are the vertex of the triangle and the midpoint of the opposite side. Median of a triangle Centroid ? 10 3 6 5

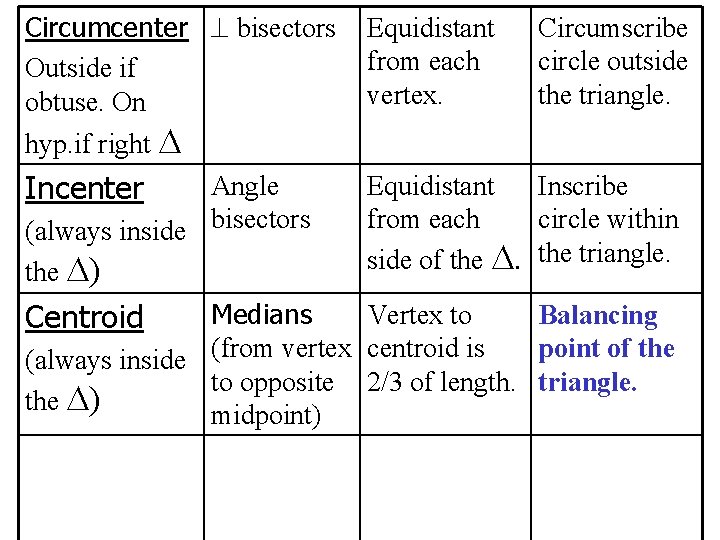
Circumcenter bisectors Outside if obtuse. On Equidistant from each vertex. Incenter Equidistant Inscribe from each circle within side of the triangle. Circumscribe circle outside the triangle. hyp. if right Angle (always inside bisectors the ) Medians Vertex to Balancing point of the (always inside (from vertex centroid is to opposite 2/3 of length. triangle. the ) midpoint) Centroid

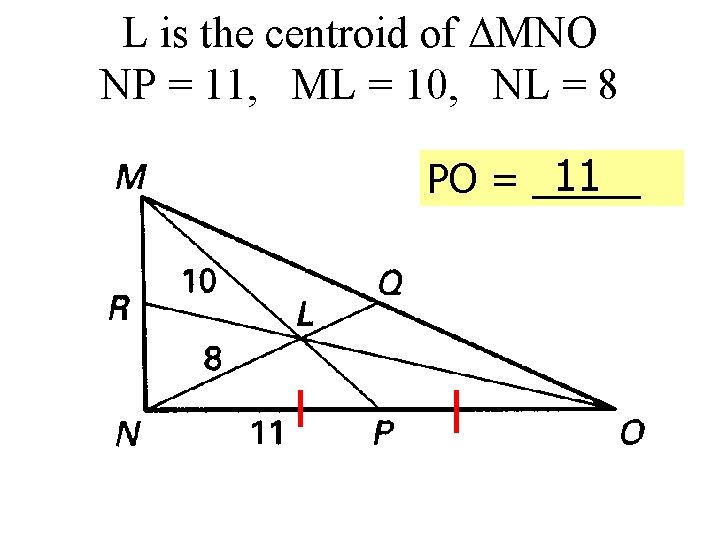
L is the centroid of MNO NP = 11, ML = 10, NL = 8 11 PO = _____

L is the centroid of MNO NP = 11, ML = 10, NL = 8 15 MP = _____ 5

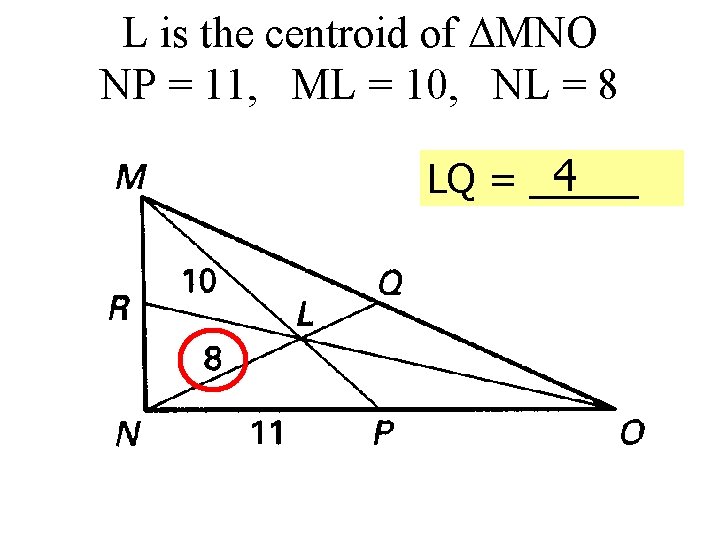
L is the centroid of MNO NP = 11, ML = 10, NL = 8 4 LQ = _____

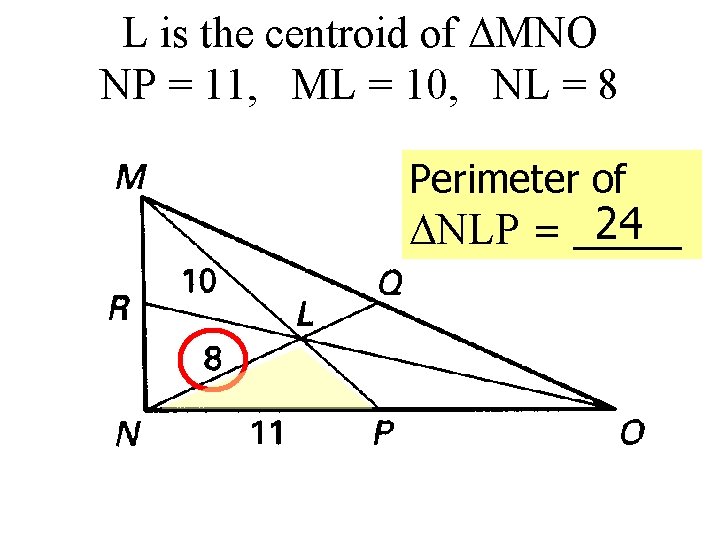
L is the centroid of MNO NP = 11, ML = 10, NL = 8 Perimeter of 24 NLP = _____

Find the coordinates of D, the midpoint of segment AB. (6, 3)

Find the length of median CD. (6, 3)

8 3

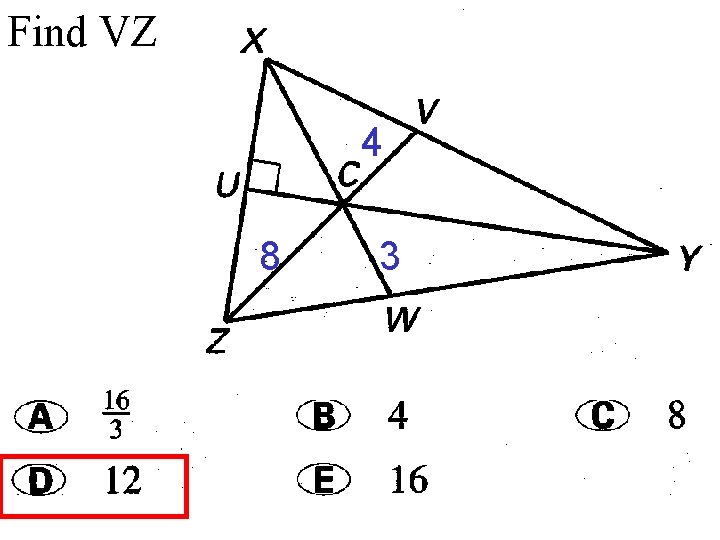
Find VZ 4 8 3

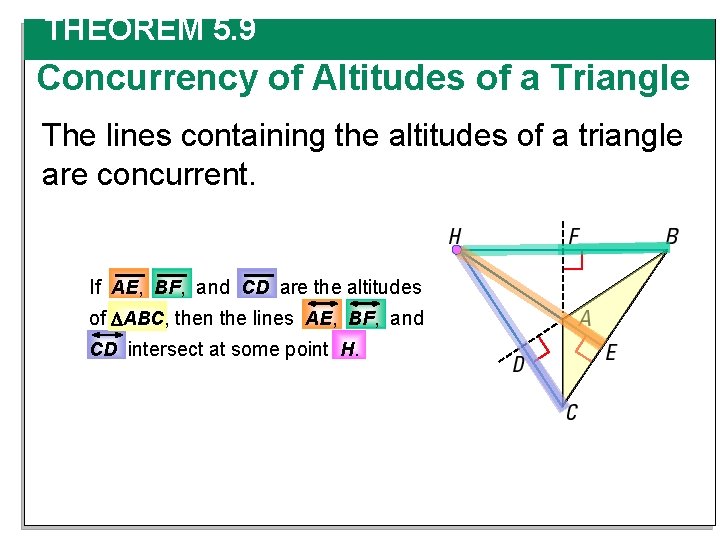
An altitude of a triangle is the perpendicular segment from a vertex to the opposite side or to the line that contains the opposite side. An altitude can lie inside, on, or outside the triangle. Every triangle has three altitudes. The lines containing the altitudes are concurrent and intersect at a point called the orthocenter of the triangle.

THEOREM 5. 9 Concurrency of Altitudes of a Triangle The lines containing the altitudes of a triangle are concurrent. If AE, BF, and CD are the altitudes of ABC, then the lines AE, BF, and CD intersect at some point H.

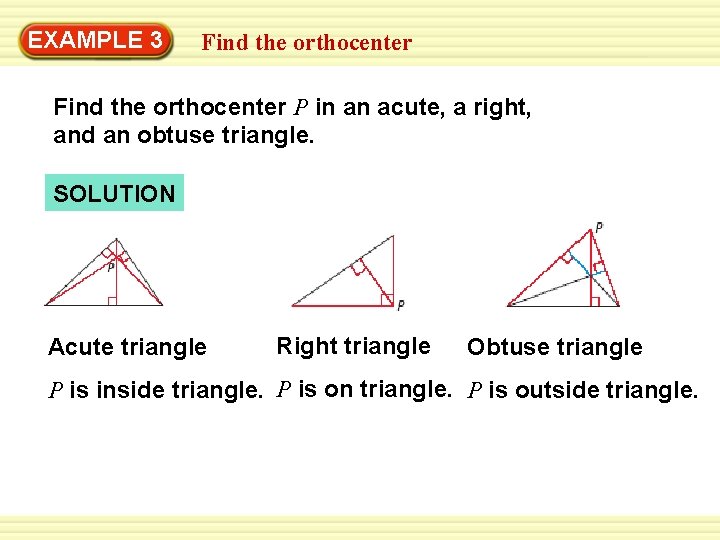
EXAMPLE 3 Find the orthocenter P in an acute, a right, and an obtuse triangle. SOLUTION Acute triangle Right triangle Obtuse triangle P is inside triangle. P is on triangle. P is outside triangle.

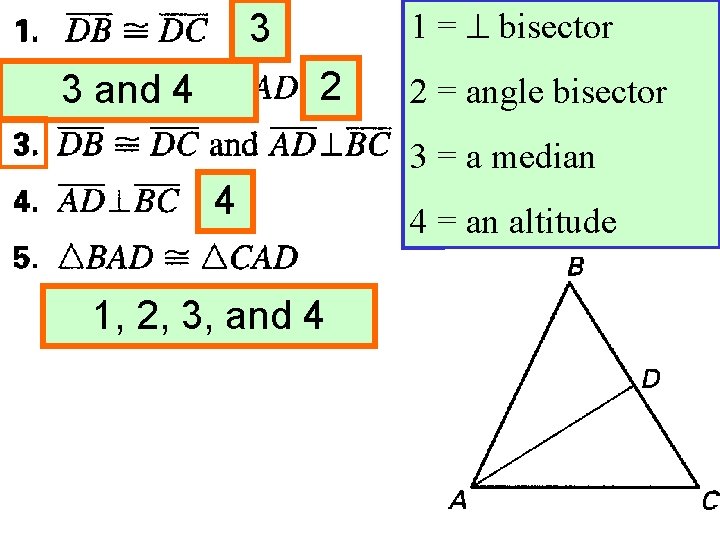
1 = bisector 3 2 3 and 4 2 = angle bisector 3 = a median 4 1, 2, 3, and 4 4 = an altitude

4 1 = bisector 2 = angle bisector 3 = a median 4 = an altitude

2 1 = bisector 2 = angle bisector 3 = a median 4 = an altitude

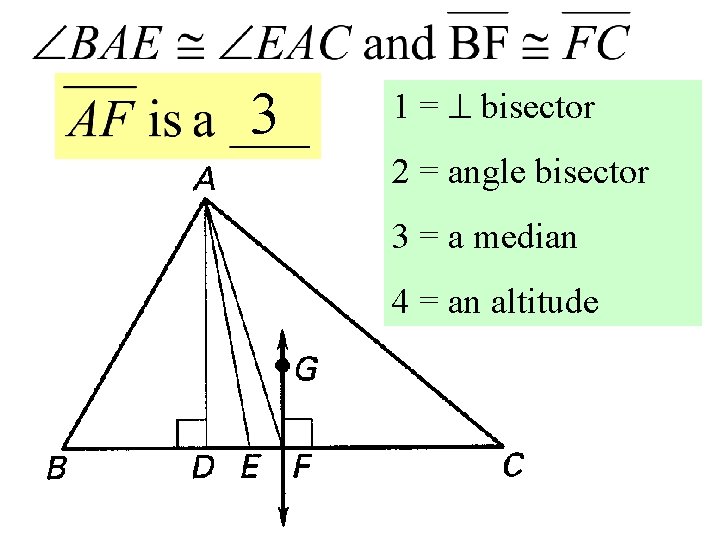
3 1 = bisector 2 = angle bisector 3 = a median 4 = an altitude

1 1 = bisector 2 = angle bisector 3 = a median 4 = an altitude

Assignment #41: Page 322 # 3 – 27, 33 – 35