5 4 The Triangle Midsegment Theorem Warm Up

5 -4 The Triangle Midsegment Theorem Warm Up Use the points A(2, 2), B(12, 2) and C(4, 8) for Exercises 1– 5. 1. Find X and Y, the midpoints of AC and CB. 2. Find XY. 3. Find AB. 4. Find the slope of AB. 5. Find the slope of XY. 6. What is the slope of a line parallel to 3 x + 2 y = 12? Holt Mc. Dougal Geometry

5 -4 The Triangle Midsegment Theorem Objective Prove and use properties of triangle midsegments. Holt Mc. Dougal Geometry

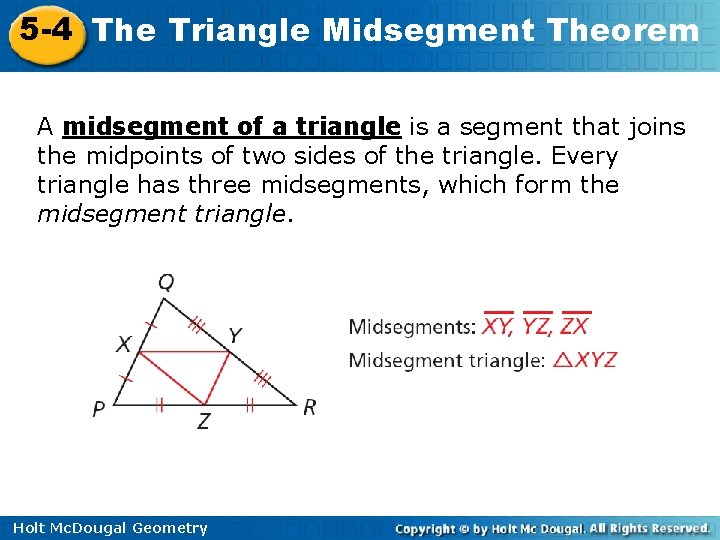
5 -4 The Triangle Midsegment Theorem A midsegment of a triangle is a segment that joins the midpoints of two sides of the triangle. Every triangle has three midsegments, which form the midsegment triangle. Holt Mc. Dougal Geometry

5 -4 The Triangle Midsegment Theorem The relationship shown in Example 1 is true for the three midsegments of every triangle. Holt Mc. Dougal Geometry

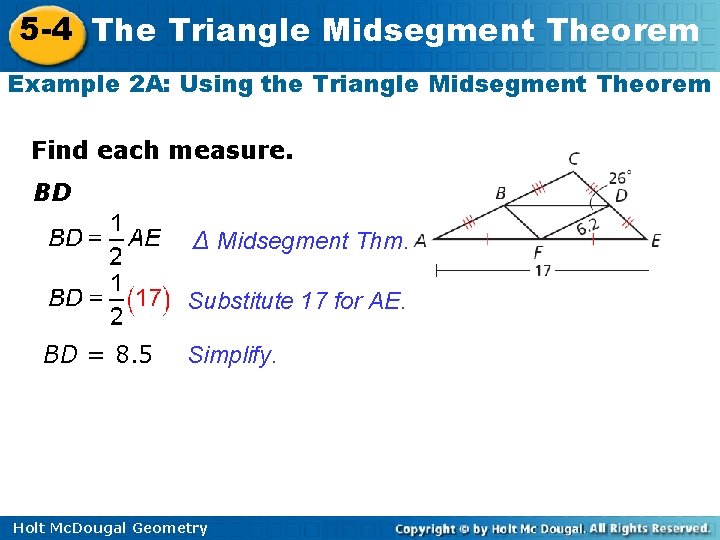
5 -4 The Triangle Midsegment Theorem Example 2 A: Using the Triangle Midsegment Theorem Find each measure. BD ∆ Midsegment Thm. Substitute 17 for AE. BD = 8. 5 Simplify. Holt Mc. Dougal Geometry

5 -4 The Triangle Midsegment Theorem Example 2 B: Using the Triangle Midsegment Theorem Find each measure. m CBD ∆ Midsegment Thm. m CBD = m BDF Alt. Int. s Thm. m CBD = 26° Holt Mc. Dougal Geometry Substitute 26° for m BDF.

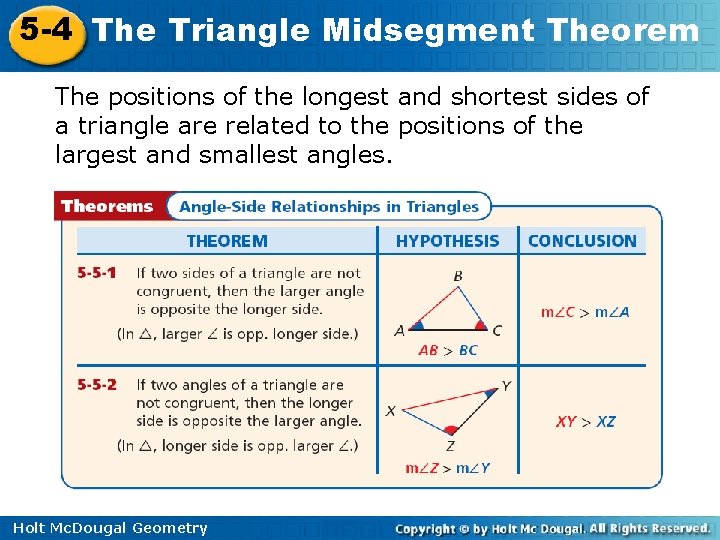
5 -4 The Triangle Midsegment Theorem The positions of the longest and shortest sides of a triangle are related to the positions of the largest and smallest angles. Holt Mc. Dougal Geometry

5 -4 The Triangle Midsegment Theorem Example 2 A: Ordering Triangle Side Lengths and Angle Measures Write the angles in order from smallest to largest. The shortest side is smallest angle is F. The longest side is , so the largest angle is G. The angles from smallest to largest are F, H and G. Holt Mc. Dougal Geometry

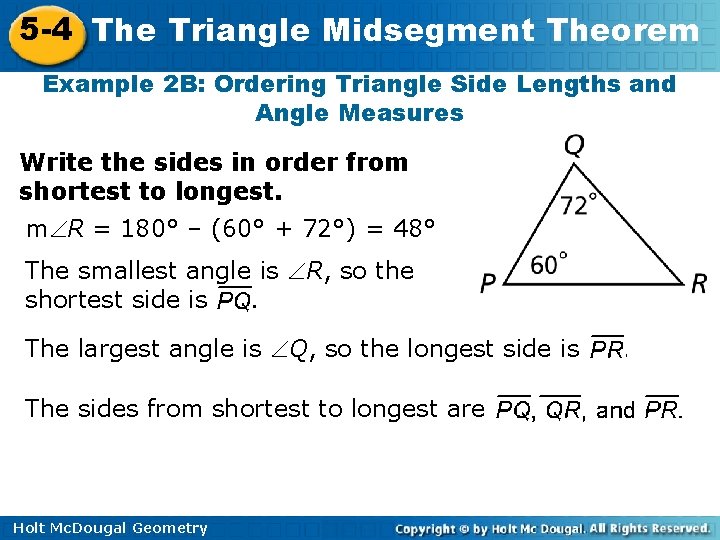
5 -4 The Triangle Midsegment Theorem Example 2 B: Ordering Triangle Side Lengths and Angle Measures Write the sides in order from shortest to longest. m R = 180° – (60° + 72°) = 48° The smallest angle is R, so the shortest side is. The largest angle is Q, so the longest side is The sides from shortest to longest are Holt Mc. Dougal Geometry .

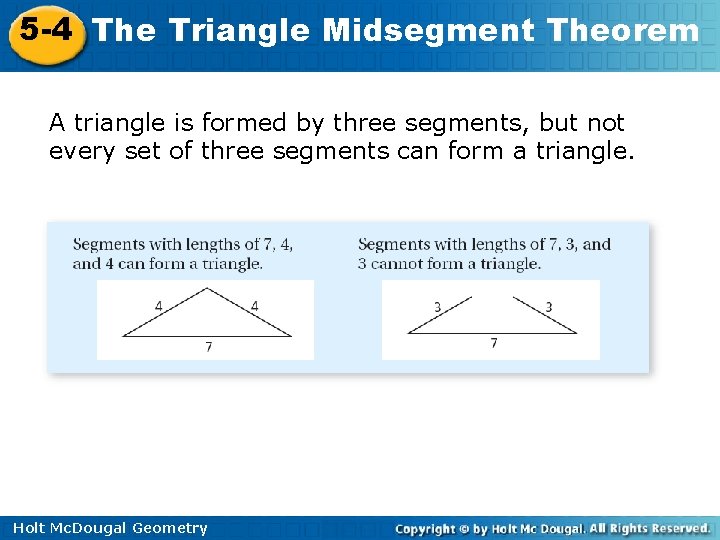
5 -4 The Triangle Midsegment Theorem A triangle is formed by three segments, but not every set of three segments can form a triangle. Holt Mc. Dougal Geometry

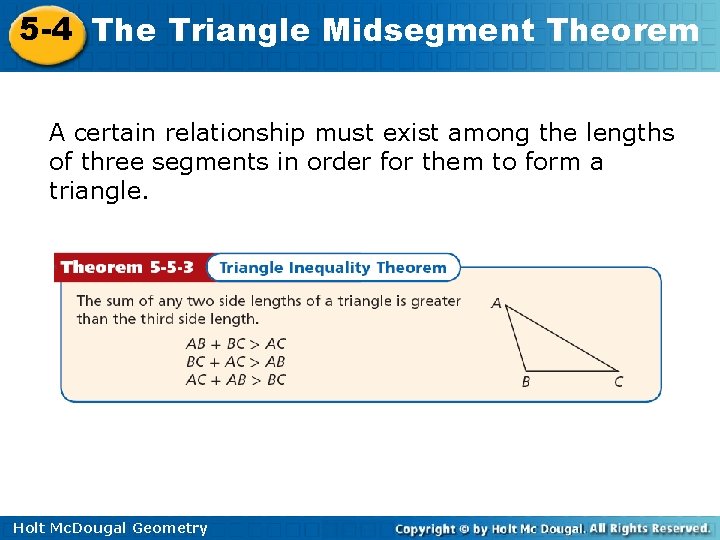
5 -4 The Triangle Midsegment Theorem A certain relationship must exist among the lengths of three segments in order for them to form a triangle. Holt Mc. Dougal Geometry

5 -4 The Triangle Midsegment Theorem Example 3 A: Applying the Triangle Inequality Theorem Tell whether a triangle can have sides with the given lengths. Explain. 7, 10, 19 No—by the Triangle Inequality Theorem, a triangle cannot have these side lengths. Holt Mc. Dougal Geometry

5 -4 The Triangle Midsegment Theorem Example 4: Finding Side Lengths The lengths of two sides of a triangle are 8 inches and 13 inches. Find the range of possible lengths for the third side. Holt Mc. Dougal Geometry

5 -4 The Triangle Midsegment Theorem Assignment • Pg. 336 (11 -26) Holt Mc. Dougal Geometry