5 4 Polynomials Vocabulary 2 1 Identify terms

5. 4 Polynomials Vocabulary 2 1 Identify terms and coefficients. 2 Know the vocabulary for polynomials.

Identify terms and coefficients. In an expression such as the quantities 4 x 3, 6 x 2, 5 x, and 8 are called terms. In the first term 4 x 3, the number 4 is called the coefficient, of x 3. In the same way, 6 is the coefficient of x 2 in the term 6 x 2, and 5 is the coefficient of x in the term 5 x. The constant term is 8. Slide 5. 4 -4

EXAMPLE 1 Identifying Coefficients Name the coefficient of each term in the expression Solution: Slide 5. 4 -5

Know the vocabulary for polynomials. A polynomial in x is a term or the sum of a finite number of terms of the form axn, for any real number a and any whole number (no negative, no fraction) n. For example, Polynomial in x is a polynomial in x. (The 4 can be written as 4 x 0. ) This polynomial is written in standard form, since the exponents on x decrease from left to right. By contrast, Not a Polynomial is not a polynomial in x, since x appears in a denominator. A polynomial can be defined using any variable and not just x. In fact, polynomials may have terms with more than one variable. Slide 5. 4 -10

Know the vocabulary for polynomials. (cont’d) The degree of a term is the sum of the exponents on the variables. For example 3 x 4 has degree 4, while the term 5 x (or 5 x 1) has degree 1, − 7 has degree 0 ( since − 7 can be written − 7 x 0). The degree of a polynomial is the greatest degree term of the polynomial. For example 3 x 4 + 5 x 2 + 6 is of degree 4. Slide 5. 4 -11

Know the vocabulary for polynomials. (cont’d) Three types of polynomials are common and given special names. A polynomial with only one term is called a monomial. (Mono- means “one, ” as in monorail. ) Examples are and Monomials A polynomial with exactly two terms is called a binomial. (Bi- means “two, ” as in bicycle. ) Examples are and Binomials A polynomial with exactly three terms is called a trinomial. (Tri- means “three, ” as in triangle. ) Examples are and Trinomials Slide 5. 4 -12

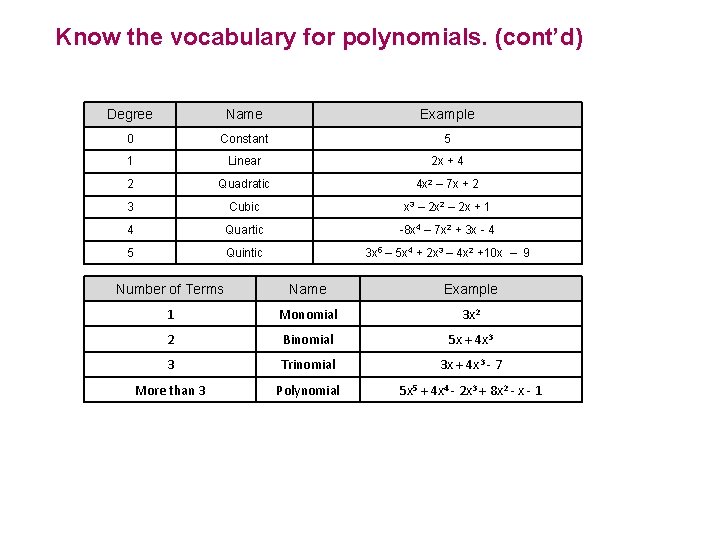
Know the vocabulary for polynomials. (cont’d) Degree Name Example 0 Constant 5 1 Linear 2 x + 4 2 Quadratic 4 x 2 – 7 x + 2 3 Cubic x 3 – 2 x 2 – 2 x + 1 4 Quartic -8 x 4 – 7 x 2 + 3 x - 4 5 Quintic 3 x 5 – 5 x 4 + 2 x 3 – 4 x 2 +10 x – 9 Number of Terms Name Example 1 Monomial 3 x 2 2 Binomial 5 x + 4 x 3 3 Trinomial 3 x + 4 x 3 - 7 More than 3 Polynomial 5 x 5 + 4 x 4 - 2 x 3 + 8 x 2 - x - 1

EXAMPLE 3 Classifying Polynomials Write polynomial in standard form, give the degree, and tell whether the polynomial is a monomial, binomial, trinomial. 3 x + 5 x 3 - 4 Solution: 5 x 3 + 3 x – 4 Degree 3 or cubic, trinomial Slide 5. 4 -13

Add like terms have exactly the same combinations of variables, with the same exponents on the variables. Only the coefficients may differ. Examples of like terms We combine, or add, like terms by adding their coefficients. Slide 5. 4 -7

EXAMPLE 2 Adding Like Terms Simplify by adding like terms. Solution: Unlike terms cannot be combined. Unlike terms have different variables or different exponents on the same variables. Slide 5. 4 -8

Add and subtract polynomials. Polynomials may be added, subtracted, multiplied, and divided. Adding Polynomials To add two polynomials, add like terms. Subtracting Polynomials To subtract two polynomials, change all the signs in the second polynomial and add the result to the first polynomial. Slide 5. 4 -17

EXAMPLE 5 Adding Polynomials Vertically Add. and Solution: + + Slide 5. 4 -18

EXAMPLE 6 Adding Polynomials Horizontally Add. Solution: Slide 5. 4 -19

EXAMPLE 7 Subtracting Polynomials Horizontally Perform the subtractions. Solution: from Slide 5. 4 -20

EXAMPLE 8 Subtracting Polynomials Vertically Subtract. Solution: + Slide 5. 4 -21

EXAMPLE 9 Adding and Subtracting Polynomials with More Than One Variable Subtract. Solution: Slide 5. 4 -22

EXAMPLE 4 Evaluating a Polynomial Find the value of 2 y 3 + 8 y − 6 when y = − 1. Solution: Use parentheses around the numbers that are being substituted for the variable, particularly when substituting a negative number for a variable that is raised to a power, or a sign error may result. Slide 5. 4 -15