5 4 Poazejev zakon 1 2 Odavde se
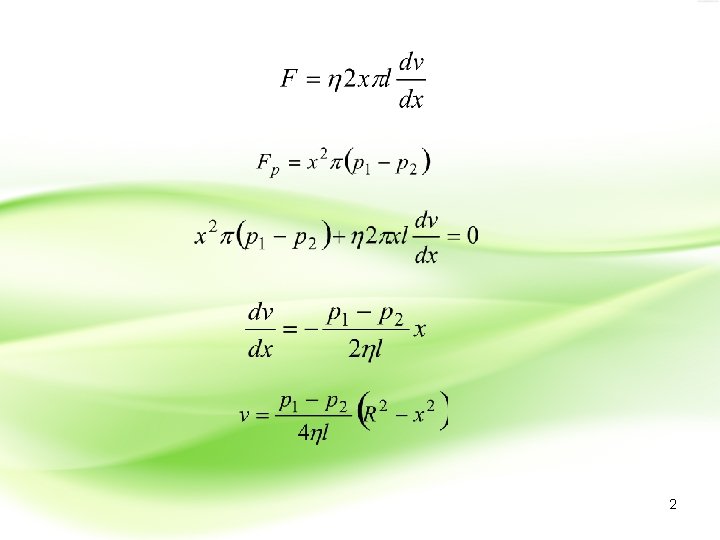











- Slides: 19

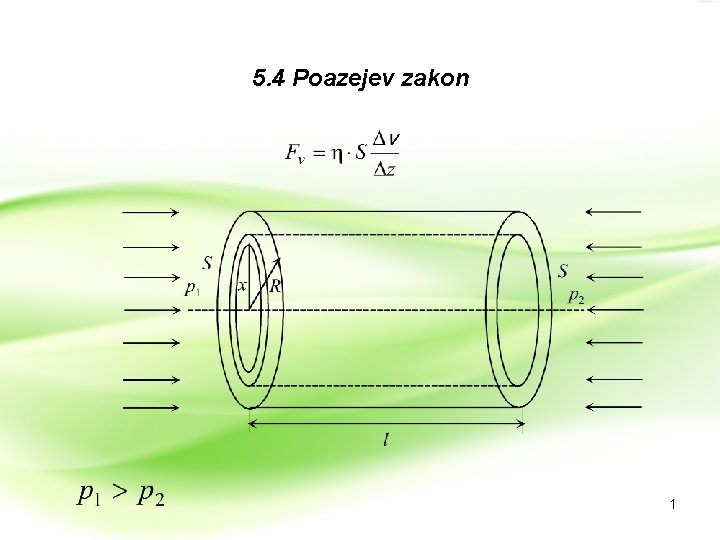
5. 4 Poazejev zakon 1
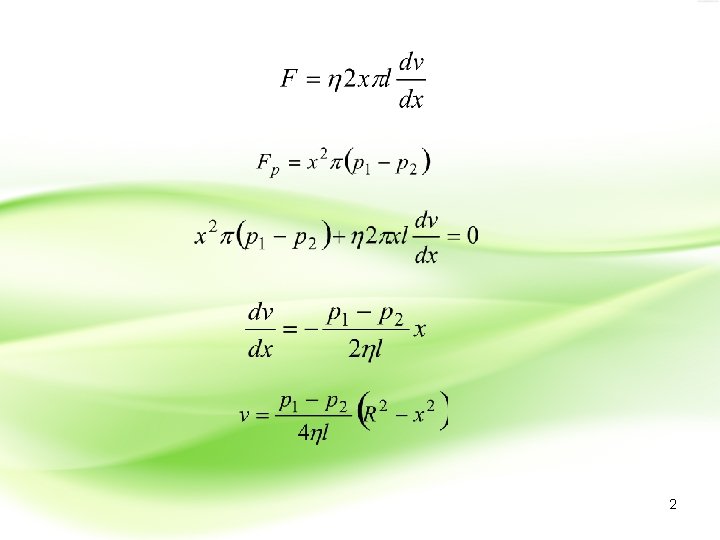
2

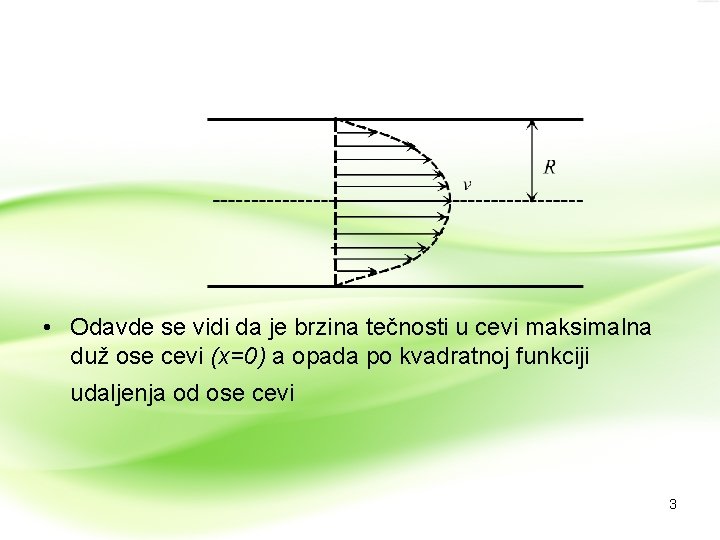
• Odavde se vidi da je brzina tečnosti u cevi maksimalna duž ose cevi (x=0) a opada po kvadratnoj funkciji udaljenja od ose cevi 3

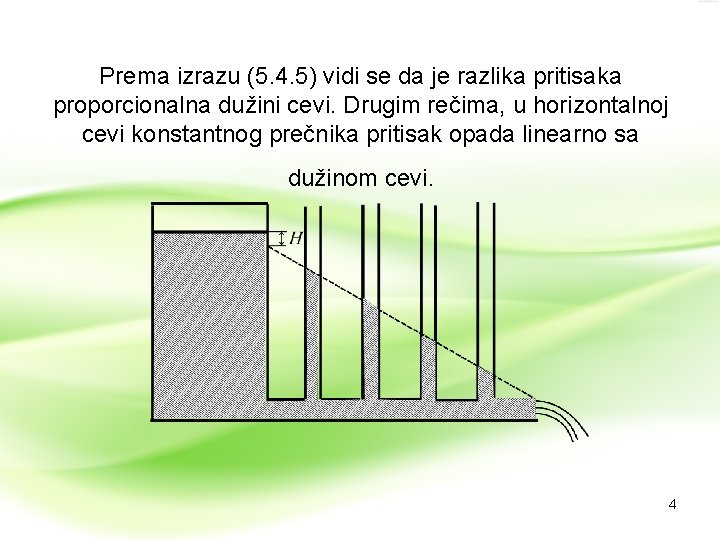
Prema izrazu (5. 4. 5) vidi se da je razlika pritisaka proporcionalna dužini cevi. Drugim rečima, u horizontalnoj cevi konstantnog prečnika pritisak opada linearno sa dužinom cevi. 4

Opadanje pritiska duž cevi može se posmatrati i sa gledišta energije. Tečnost ima konstantnu brzinu duž cevi, te se njena kinetička energija ne može menjati duž cevi. Pošto je kretanje tečnosti u horizontalnom pravcu, tečnost ne dobija nikakav rad od gravitacionog polja. Međutim, da bi se tečnost kretala, mora se savlađivati sila trenja i time vršiti rad. Prema opisanim uslovima ovaj rad može da se vrši samo na račun energije pritiska, te on mora opadati. 5

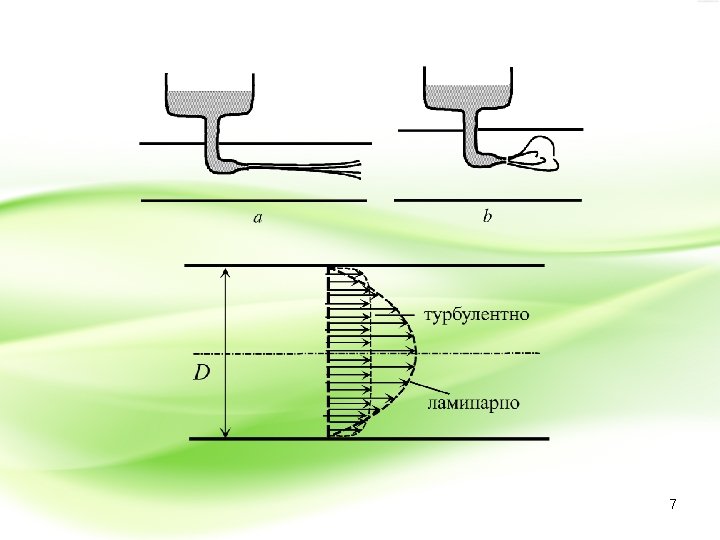
5. 5 Turbulentno kretanje i Rejnoldsov broj • Međutim, pri većim brzinama strujanja fluida javlja se mešanje strujnica, pri čemu ne postoji više kretanje po slojevima, već se slojevi međusobno mešaju formirajući veoma složene oblike koji su mahom nepravilni i ne mogu se lako posmatrati. Takvo strujanje se naziva turbulentno strujanje. Do koje će granice postojati laminarno strujanje i kada će nastupiti turbulentno kretanje zavisi od vrlo mnogo okolnosti, koje se jednostavnom teorijom ne mogu predvideti. Uglavnom se turbulentno strujanje javlja pri većim brzinama, ali granica brzine zavisi i od prečnika mlaza, oblika suda i obrade površine suda kroz koji struji tečnost. U nekim okolnostima i mali potresi ili beznačajni uzroci mogu da izazovu prelaz laminarnog kretanja u turbulentno. 6

7

Rejnoldsov kriterijum ili Rejnoldsov (Osborne Reynolds) broj: • Skoro uvek turbulentno kretanje • U granicama od 2000 do 3000 kretanje može biti i turbulentno i laminarno što zavisi od pomenutih složenih faktora čije se gradacije ustanovljuju empirijskim putem i obično izražavaju pomoću tablica. Iz izraza za Rejnoldsov broj dobija se kritična brzina za vodu kada protiče kroz cev prečnika a pri temperaturi od 8

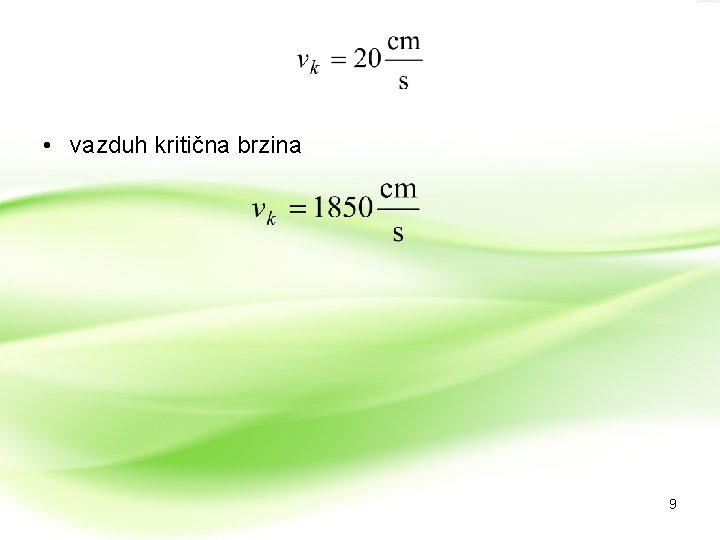
• vazduh kritična brzina 9

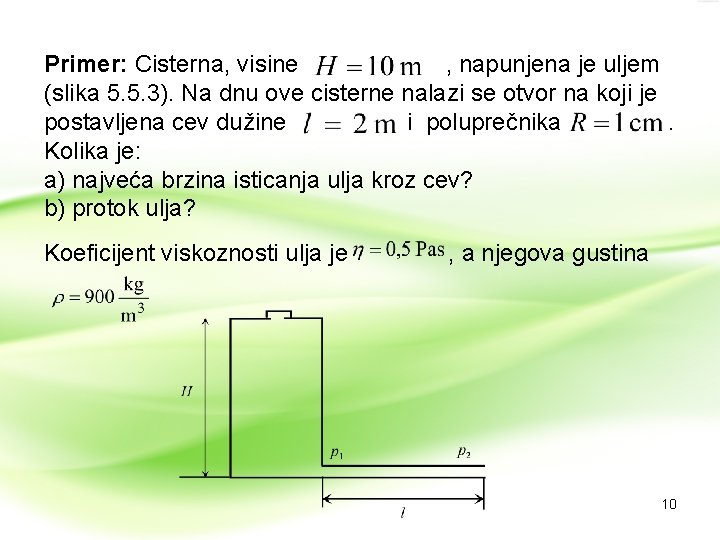
Primer: Cisterna, visine , napunjena je uljem (slika 5. 5. 3). Na dnu ove cisterne nalazi se otvor na koji je postavljena cev dužine i poluprečnika. Kolika je: a) najveća brzina isticanja ulja kroz cev? b) protok ulja? Koeficijent viskoznosti ulja je , a njegova gustina 10

Najveća brzina 11

Primer: Metalna cev, dužine i poluprečnika spojena je na javnu vodovodnu mrežu, u kojoj je pritisak vode. Voda na drugom kraju ističe slobodno. Atmosferski pritisak je , a viskoznost vode. Koliki je protok vode kroz cev? 12

• Primer: Da bi se odredila viskoznost alkohola, meri se masa isteklog alkohola kroz horizontalnu kapilarnu cev, dužine i prečnika , pod dejstvom pritiska stuba alkohola visine. Za vreme istekne količina alkohola čija je masa. Kolika je viskoznost alkohola prema ovim podacima ako je njegova gustina ? 13

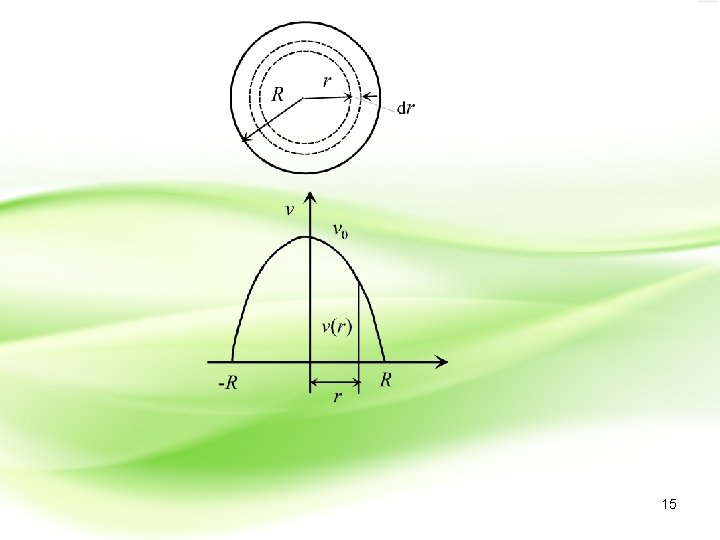
• Primer: Kroz cev, dužine i poluprečnika , protiče tečnost gustine i viskoznosti. Brzina proticanja tečnosti određena je relacijom: gde je brzina tečnosti na sredini cevi, a poluprečnik uočenog cilindričnog sloja tečnosti. • a) Koliki je protok tečnosti kroz cev? • b) Kolika je kinetička energija tečnosti u cevi? • c) Kolika je sila trenja između cevi i tečnosti? • d) Kolika je razlika pritisaka na krajevima cevi? 14

15

a) Protok tečnosti kroz elementarnu poprečnu površinu je • b)Kinetička energija jednog sloja tečnosti, mase čija je brzina , je , 16

• v) Prema Njutnovom zakonu unutrašnjeg trenja je 17

• d) Prema Poazjeovom zakonu je 18

1. Pritisak u fluidu 2. Protok fluida i jednačina kontinuiteta • 1. Strujnom cevi protiče voda (gustine 1000 kg/m 3). Na jednom poprečnom preseku, čiji centar se nalazi na visini 2 m iznad horizonta, brzina proticanja je 2 m/s, a pritisak koji na njemu vlada 1, 4 105 Pa. Kolika je brzina proticanja tečnosti na drugom poprečnom preseku koji se nalazi na visini 1 m iznad horizonta a na kome vlada pritisak 1, 2 105 Pa? Za ubrzanje sile Zemljine teže uzeti 10 m/s 2. • 2. Kugla, načinjena od homogene supstancije gustine , pliva između dve tečnosti koje se ne mešaju. Gustina gornje tečnosti je , a donje. Koliki deo kugle je potopljen u gornju, a koliki u donju tečnost? 19