5 4 Isosceles and Equilateral Triangles Geometry What

5. 4 Isosceles and Equilateral Triangles Geometry What conjectures can you make about congruent angles and sides?

Topic/Objective Use properties of isosceles triangles. n Use properties of equilateral triangles. n 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 2

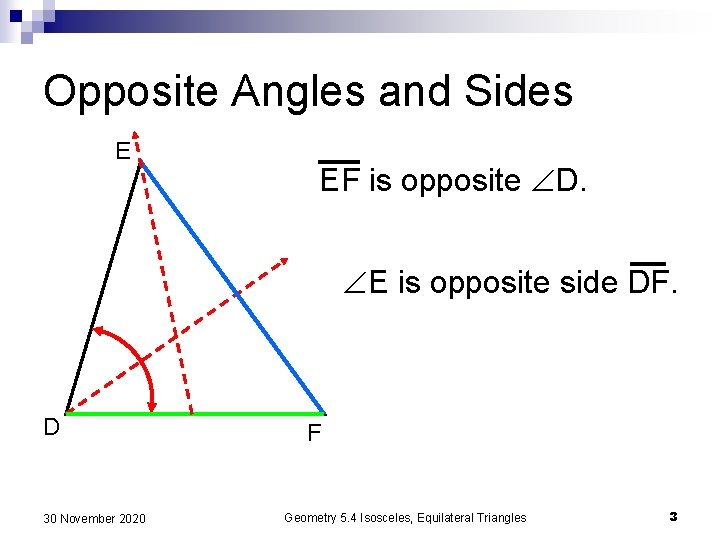
Opposite Angles and Sides E EF is opposite D. E is opposite side DF. D 30 November 2020 F Geometry 5. 4 Isosceles, Equilateral Triangles 3

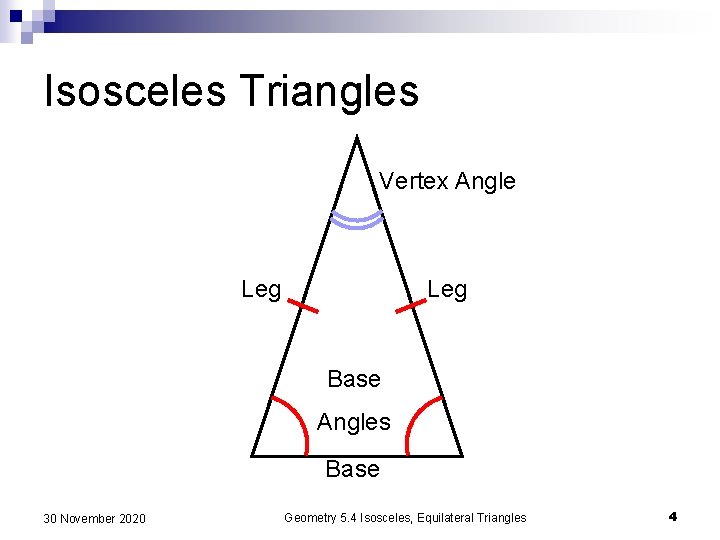
Isosceles Triangles Vertex Angle Leg Base Angles Base 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 4

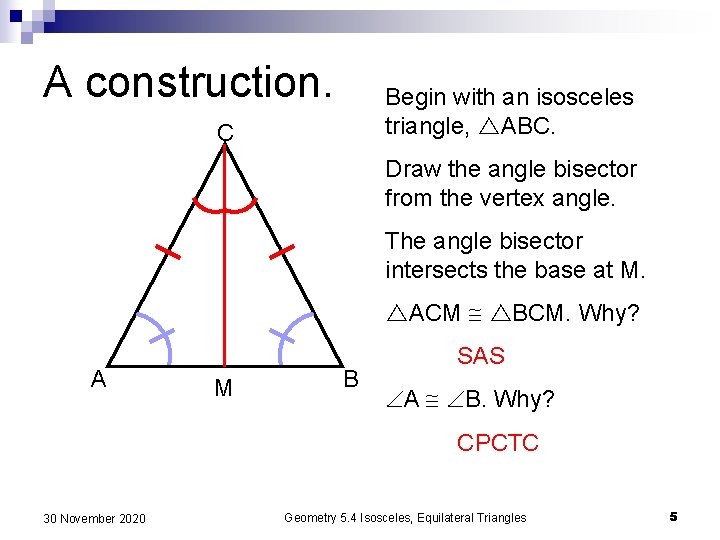
A construction. Begin with an isosceles triangle, ABC. C Draw the angle bisector from the vertex angle. The angle bisector intersects the base at M. ACM BCM. Why? A M B SAS A B. Why? CPCTC 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 5

Theorem 5. 6 Base Angles Theorem. If two sides of a triangle are congruent, then the angles opposite them are congruent. n (Easy form) The base angles of an isosceles triangle are congruent. n 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 6

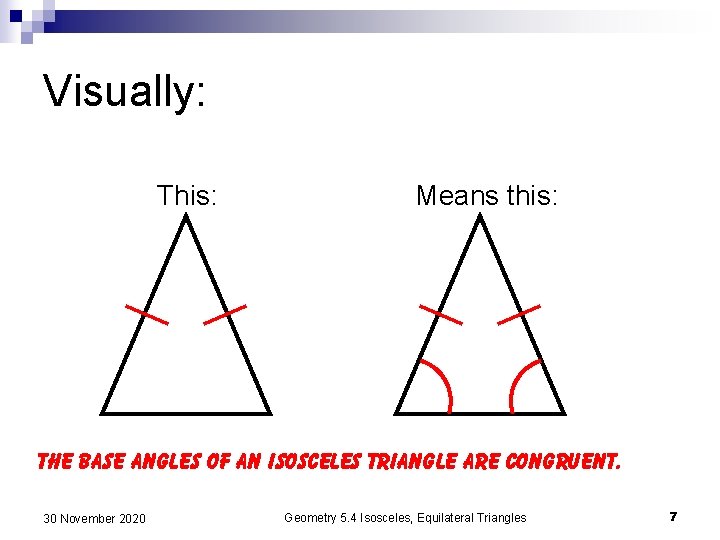
Visually: This: Means this: The base angles of an isosceles triangle are congruent. 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 7

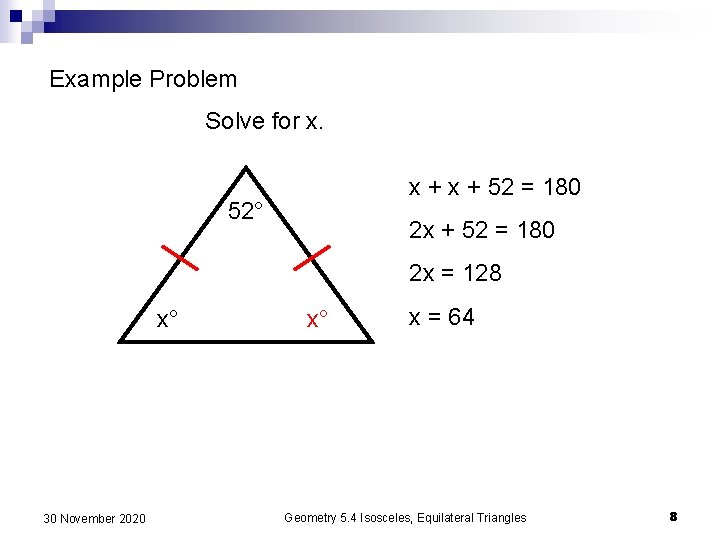
Example Problem Solve for x. x + 52 = 180 52° 2 x + 52 = 180 2 x = 128 x° 30 November 2020 x° x = 64 Geometry 5. 4 Isosceles, Equilateral Triangles 8

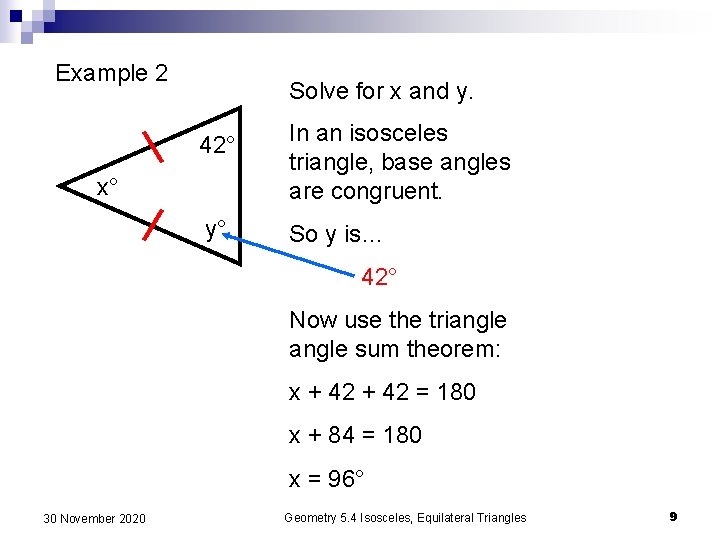
Example 2 Solve for x and y. 42° x° y° In an isosceles triangle, base angles are congruent. So y is… 42° Now use the triangle sum theorem: x + 42 = 180 x + 84 = 180 x = 96° 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 9

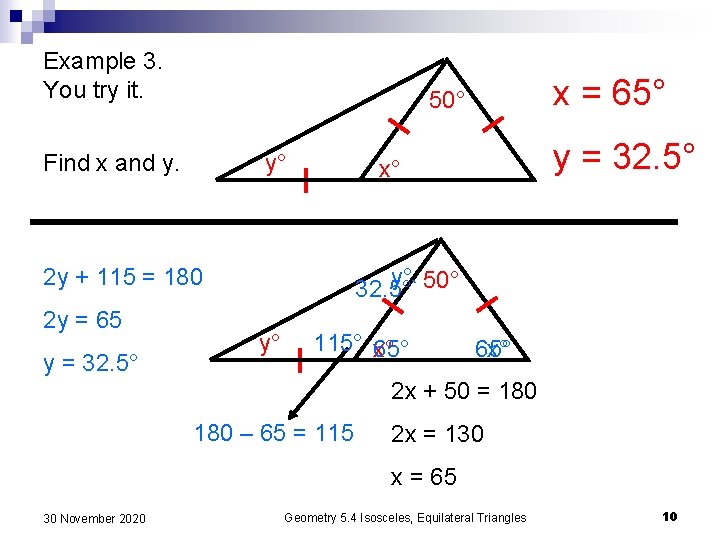
Example 3. You try it. Find x and y. y° y = 32. 5° x° 2 y + 115 = 180 2 y = 65 x = 65° 50° y° 50° 32. 5°` y° 115° 65° x° 2 x + 50 = 180 – 65 = 115 2 x = 130 x = 65 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 10

Example 4 Solve for x. (2 x)° 3 x – 25 = 2 x x = 25 (3 x – 25)° 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 11

Theorem 5. 7 Converse of the Base Angles Theorem. n If two angles of a triangle are congruent, then the sides opposite them are congruent. n 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 12

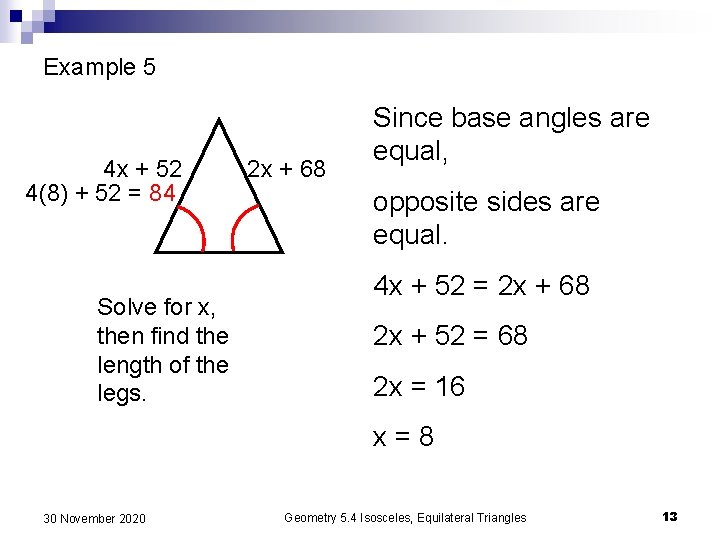
Example 5 4 x + 52 4(8) + 52 = 84 Solve for x, then find the length of the legs. 2 x + 68 Since base angles are equal, opposite sides are equal. 4 x + 52 = 2 x + 68 2 x + 52 = 68 2 x = 16 x=8 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 13

Example 6 You do it. Find the length of each side. 40 4 x – 2 5 x 30 5 x = 3 x + 16 2 x = 16 x=8 3 x + 16 40 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 14

Equilateral Triangles Corollaries to Base Angles Theorem If a triangle is equilateral, then it is also equiangular. n If a triangle is equiangular, then it is also equilateral. n 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 15

30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 16

Example 7 All sides are congruent. Solve for x. 3 x – 10 = x + 10 2 x = 20 3 x – 10 x + 10 x = 10 2 x = x + 10 x = 10 2 x 3 x – 10 = 2 x x – 10 = 0 x = 10 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 17

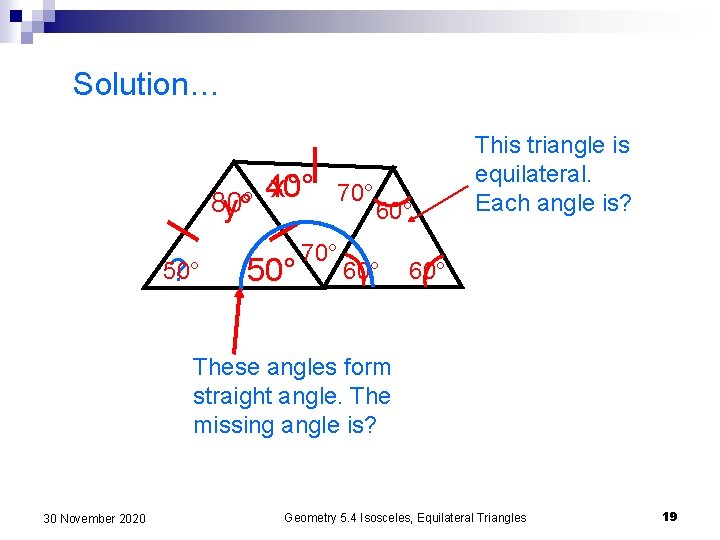
One last problem. Solve for x and y. y° x° 50° Solution… 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 18

Solution… 80° y° 50° ? 40° x° 50° 70° 60° This triangle is equilateral. Each angle is? 60° These angles form straight angle. The missing angle is? 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 19

Summarize what you have learned today n The base angles of an isosceles triangle are congruent. n Equilateral triangles are Equiangular. 30 November 2020 Geometry 5. 4 Isosceles, Equilateral Triangles 20