5 3 Vocabulary included angle triangle rigidity SAS

5. 3 Vocabulary included angle triangle rigidity SAS Triangle Congruence

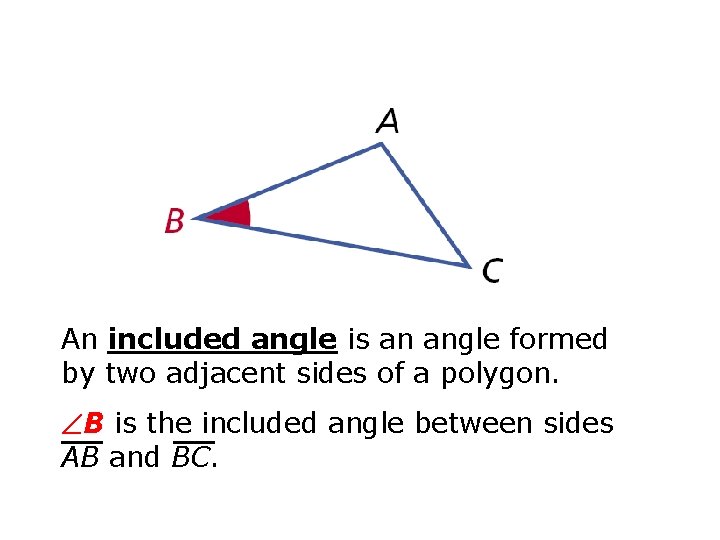
An included angle is an angle formed by two adjacent sides of a polygon. B is the included angle between sides AB and BC.

In Lesson 5 -2, you proved triangles congruent by showing that all six pairs of corresponding parts were congruent. The property of triangle rigidity gives you a shortcut for determining two triangles congruent. It allows that if certain combinations of angles and sides are congruent then the triangles are congruent.

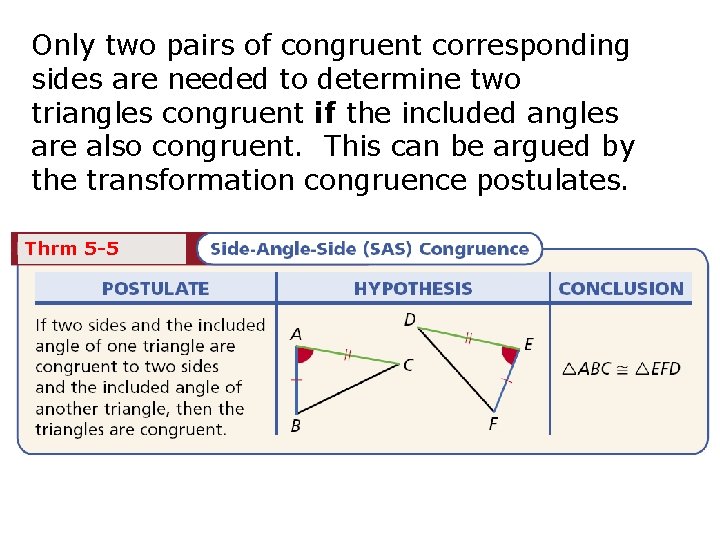
Only two pairs of congruent corresponding sides are needed to determine two triangles congruent if the included angles are also congruent. This can be argued by the transformation congruence postulates. Thrm 5 -5

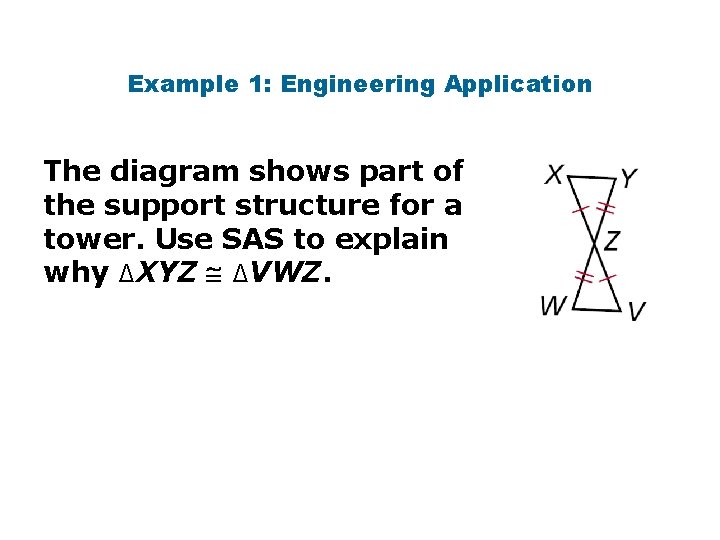
Example 1: Engineering Application The diagram shows part of the support structure for a tower. Use SAS to explain why ∆XYZ ∆VWZ.

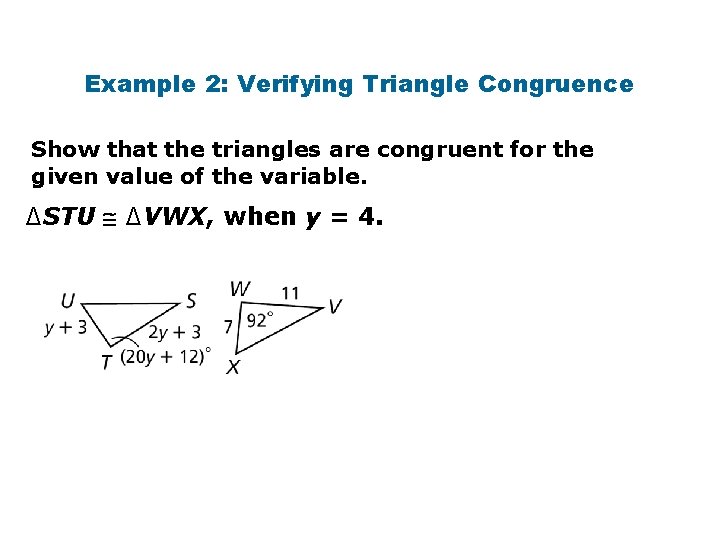
Example 2: Verifying Triangle Congruence Show that the triangles are congruent for the given value of the variable. ∆STU ∆VWX, when y = 4.

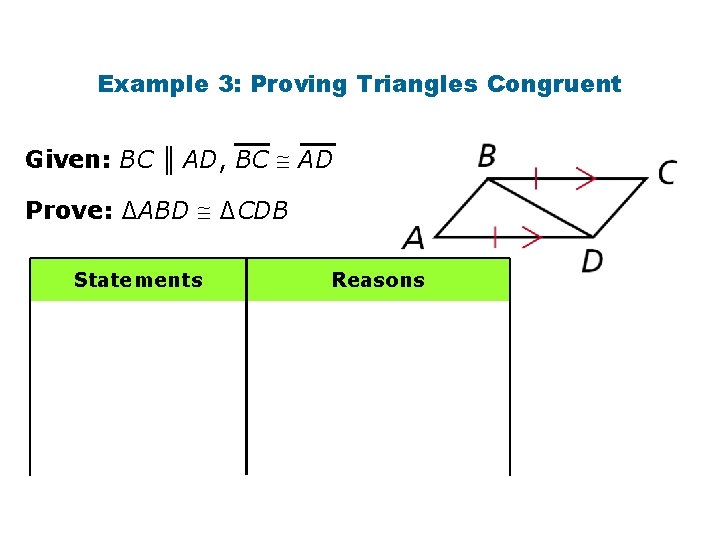
Example 3: Proving Triangles Congruent Given: BC ║ AD, BC AD Prove: ∆ABD ∆CDB Statements Reasons

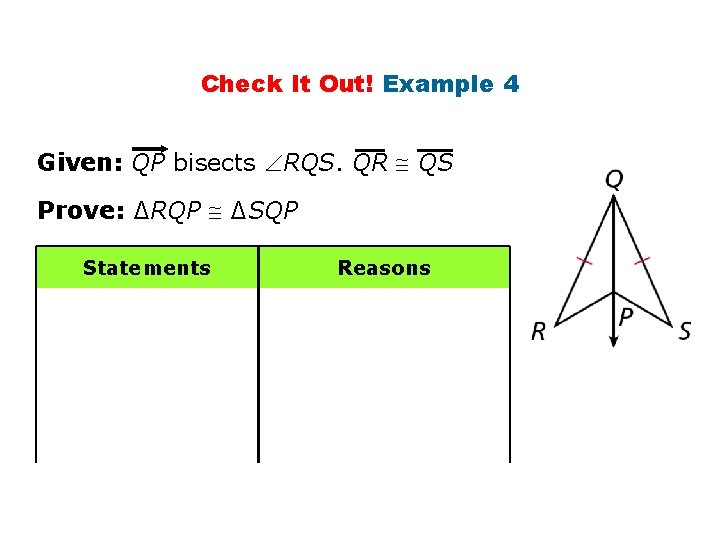
Check It Out! Example 4 Given: QP bisects RQS. QR QS Prove: ∆RQP ∆SQP Statements Reasons

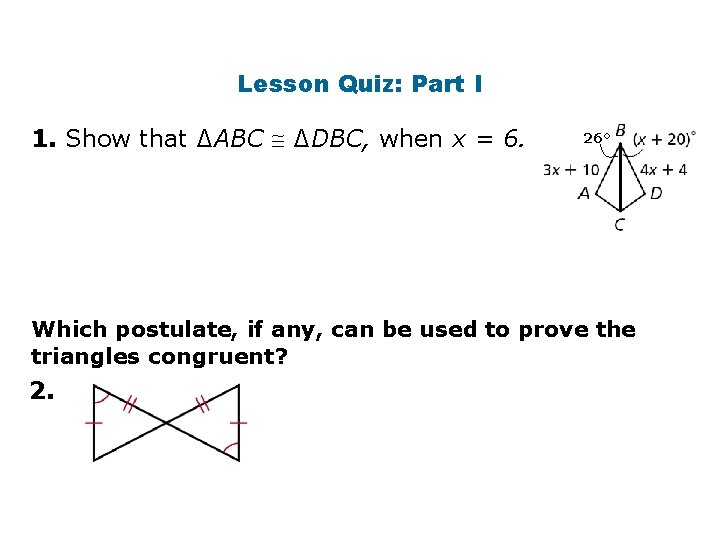
Lesson Quiz: Part I 1. Show that ∆ABC ∆DBC, when x = 6. 26° Which postulate, if any, can be used to prove the triangles congruent? 2.

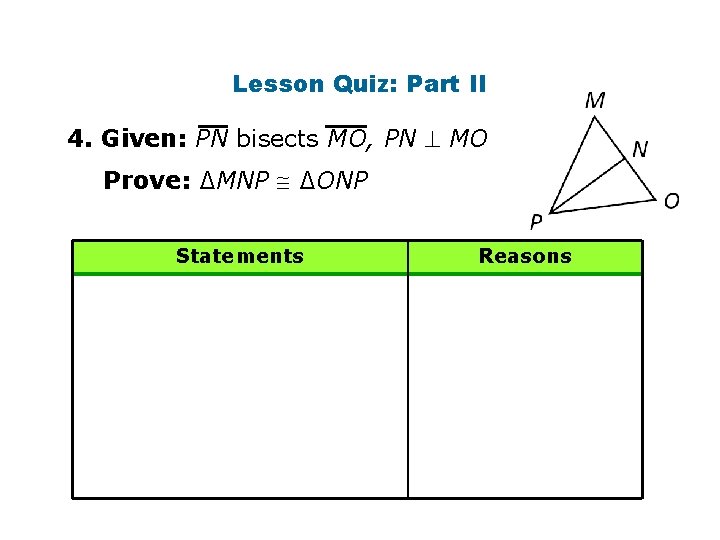
Lesson Quiz: Part II 4. Given: PN bisects MO, PN MO Prove: ∆MNP ∆ONP Statements Reasons

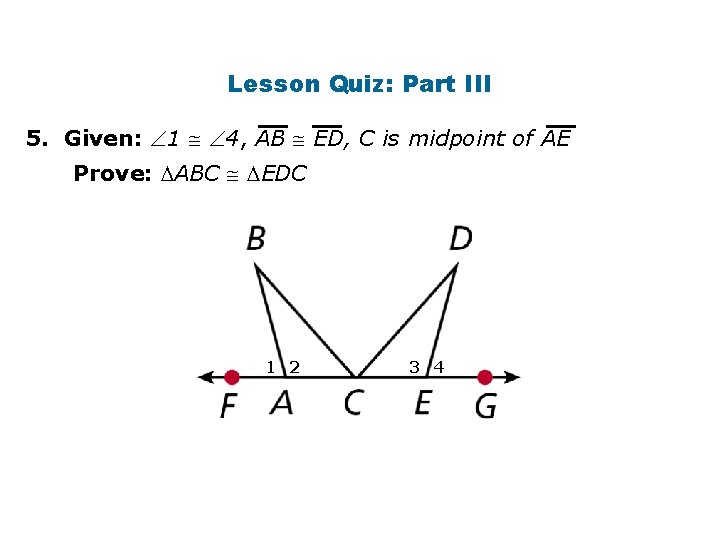
Lesson Quiz: Part III 5. Given: 1 4, AB ED, C is midpoint of AE Prove: ABC EDC 1 2 3 4