5 3 Orthogonal Transformations This picture is from

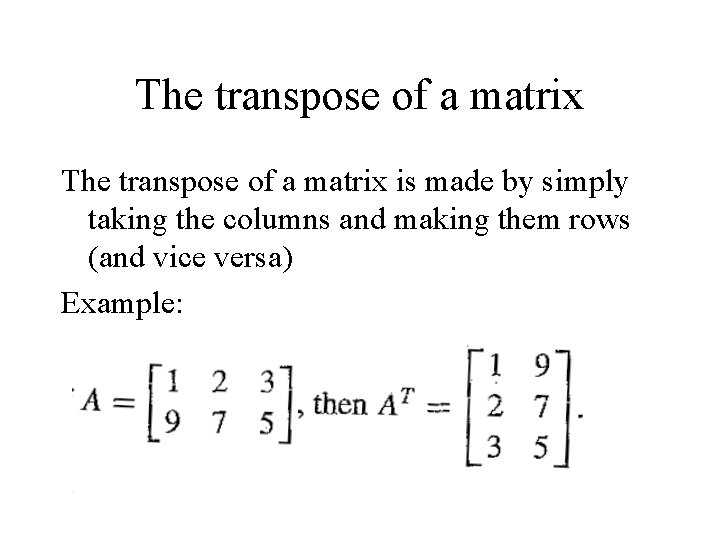












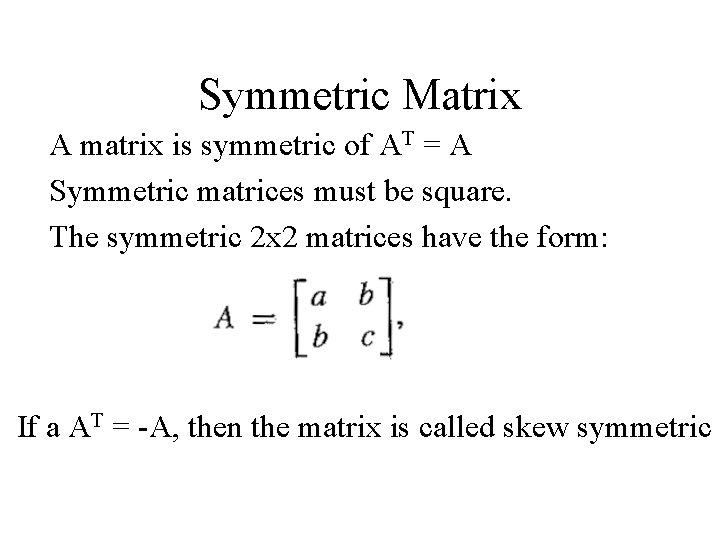









- Slides: 26

5. 3 Orthogonal Transformations This picture is from knot theory

Recall
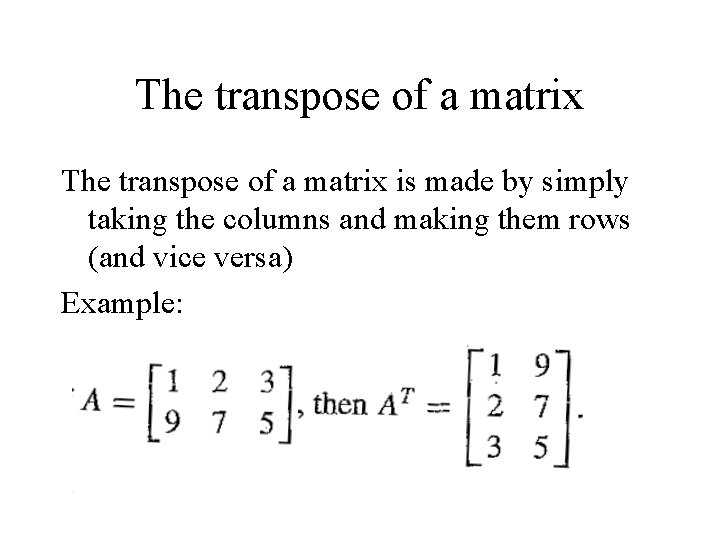
The transpose of a matrix is made by simply taking the columns and making them rows (and vice versa) Example:

Properties of orthogonal matrices (Q) An orthogonal matrix (probably better name would be orthonormal). Is a matrix such that each column vector is orthogonal to ever other column vector in the matrix. Each column in the matrix has length 1. We created these matrices using the Gram – Schmidt process. We would now like to explore their properties.

Properties of Q Note: Q is a notation to denote that some matrix A is orthogonal QT Q = I (note: this is not normally true for QQT) If Q is square, then QT = Q-1 The Columns of Q form an orthonormal basis of Rn The transformation Qx=b preserves length (for every x entered in the equation the resulting b vector is the same length. (proof is in the book on page 211) The transformation Q preserves orthogonality (proof on next slide)

Orthogonal transformations preserve orthogonality Why? If distances are preserved then an angle that is a right angle before the transformation must still be right triangle after the transformation due to the Pythagorean theorem.

Example 1 Is the rotation an orthogonal transformation?

Solution to Example 1 Yes, because the vectors are orthogonal

Orthogonal transformations and orthogonal bases 1) A linear transformation R from Rn to Rn is orthogonal if and only if the vectors form an orthonormal basis of Rn 2) An nxn matrix A is orthogonal if and only if its columns form an orthonormal bases of Rn

Problems 2 and 4 Which of the following matrices are orthogonal?

Solutions to 2 and 4

Properties of orthogonal matrices The product AB of two orthogonal nxn matrices is orthogonal The inverse A-1 of an orthogonal nxn matrix A is orthogonal If we multiply an orthogonal matrix times a constant will the result be an orthogonal matrix? Why?

Problems 6, 8 and 10 If A and B represent orthogonal matrices, which of the following are also orthogonal? 6. -B 8. A + B 10. B-1 AB

Solutions to 6, 8 and 10 The product to two orthogonal matrices is orthogonal The inverse of an orthogonal nxn matrix is orthogonal

Properties of the transpose
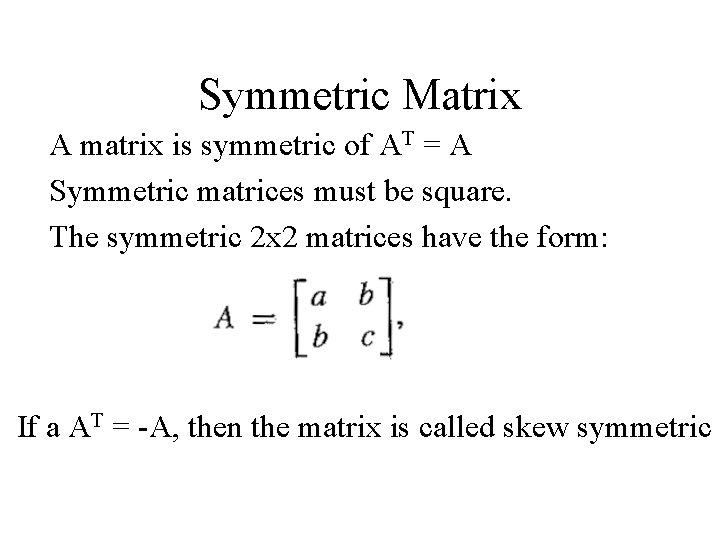
Symmetric Matrix A matrix is symmetric of AT = A Symmetric matrices must be square. The symmetric 2 x 2 matrices have the form: If a AT = -A, then the matrix is called skew symmetric

Proof of transpose properties

Problems 14, 16, 18 If A and B are symmetric and B is invertible. Which of the following must be symmetric as well? 14. –B 16. A + B

Solutions to 14, 16, 18

Problems 22 and 24 A and B are arbitrary nxn matrices. Which of the following must be symmetric? 22. BBT 24. ATBA

Solutions to 22 and 24 ATBA

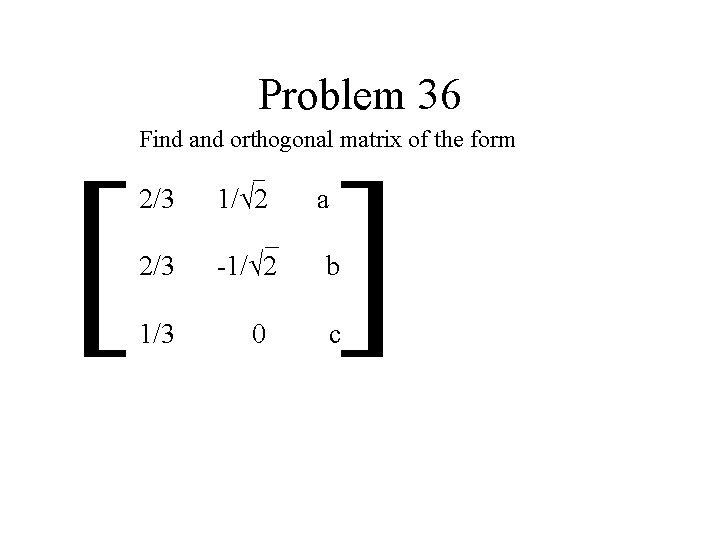
Problem 36 [ Find and orthogonal matrix of the form _ 2/3 1/3 1/√ 2 _ -1/√ 2 0 a ] b c

Problem 36 Solution

Homework: p. 218 1 -25 odd, 33 -37 all A student was learning to work with Orthogonal Matrices (Q) He asked his another student to help him learn to do operations with them: Student 1: What is 7 Q + 3 Q? Student 2: 10 Q Student 1: You’re Welcome (Question: Is 10 Q an orthogonal matrix? )

Proof – Q preserves orthogonality See next slide for a picture

Orthogonal Transformations and Orthogonal matrices A linear transformation T from Rn to Rn is called orthogonal if it preserves the lengths of vectors. ||T(x)|| = ||x|| If T(x) is an orthogonal transformation then we say that A is an orthonormal matrix.