5 2 LOGARITHMS AND EXPONENTIAL MODELS 1 Using










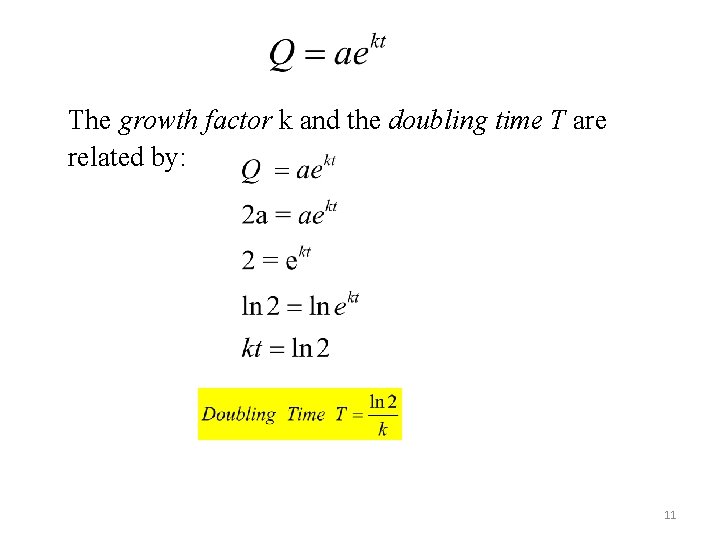
- Slides: 11

5. 2 LOGARITHMS AND EXPONENTIAL MODELS 1

Using Logarithms to Undo Exponents Example 2 The US population, P, in millions, is currently growing according to the formula P = 299 e 0. 009 t, where t is in years since 2006. When is the population predicted to reach 350 million? Solution We want to solve the following equation for t: 299 e 0. 009 t = 350. The US population is predicted to reach 350 million during the year 2024. 2

Doubling Time Example 4 (a) Find the time needed for the turtle population described by the function P = 175(1. 145)t to double its initial size. Solution (a) The initial size is 175 turtles; doubling this gives 350 turtles. We need to solve the following equation for t: 175(1. 145)t = 350 1. 145 t = 2 log 1. 145 t = log 2 t · log 1. 145 = log 2 t = log 2/log 1. 145 ≈ 5. 119 years. Note that 175(1. 145)5. 119 ≈ 350 3

Since the growth rate is 0. 000121, the growth rate factor is b = 1 – 0. 000121 = 0. 999879. Thus after t years the amount left will be 4

5

Half-Life Example 8 The quantity, Q, of a substance decays according to the formula Q = Q 0 e−kt, where t is in minutes. The half-life of the substance is 11 minutes. What is the value of k? Solution We know that after 11 minutes, Q = ½ Q 0. Thus, solving for k, we get Q 0 e−k· 11 = ½ Q 0 e− 11 k = ½ − 11 k = ln ½ / (− 11) ≈ 0. 06301, so k = 0. 063 per minute. This substance decays at the continuous rate of 6. 301% per minute. 6

Converting Between Q = a bt and Q = a ekt Any exponential function can be written in either of the two forms: Q = a bt or Q = a ekt. If b = ek, so k = ln b, the two formulas represent the same function. 7

Converting Between Q = a bt and Q = a ekt Example 9 Convert the exponential function P = 175(1. 145)t to the form P = aekt. Solution The parameter a in both functions represents the initial population. For all t, 175(1. 145)t = 175(ek)t, so we must find k such that ek = 1. 145. Therefore k is the power of e which gives 1. 145. By the definition of ln, we have k = ln 1. 145 ≈ 0. 1354. Therefore, P = 175 e 0. 1354 t. Example 10 Convert the formula Q = 7 e 0. 3 t to the form Q = a bt. Solution Using the properties of exponents, Q = 7 e 0. 3 t = 7(e 0. 3)t. Using a calculator, we find e 0. 3 ≈ 1. 3499, so Q = 7(1. 3499)t. 8

Exponential Growth Problems That Cannot Be Solved By Logarithms Example 13 With t in years, the population of a country (in millions) is given by P = 2(1. 02)t, while the food supply (in millions of people that can be fed) is given by N = 4+0. 5 t. Determine the year in which the country first experiences food shortages. Finding the intersection of linear and exponential graphs Solution Setting P = N, we get 2(1. 02)t = 4+0. 5 t, Population which, after dividing by 2 and taking (millions) the log of both sides can simplify to t log 1. 02 = log(2 + 0. 25 t). We cannot solve this equation algebraically, but we can estimate its solution numerically or graphically: t ≈ 199. 381. So it will be nearly 200 years before shortages are experienced Shortages start → N = 4+0. 5 t P = 2(1. 02)t t, years 9

The growth factor b and the doubling time T are related by: 10
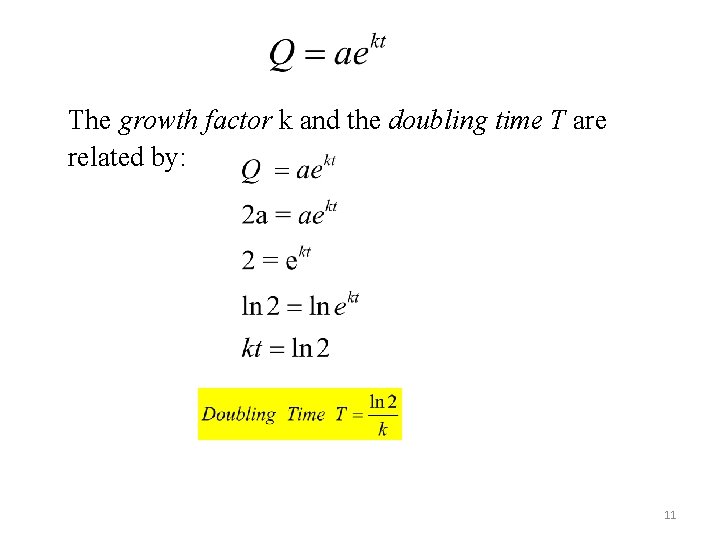
The growth factor k and the doubling time T are related by: 11
 Logarithmic to exponential form
Logarithmic to exponential form Exponential and logarithmic models
Exponential and logarithmic models Linear vs quadratic vs exponential
Linear vs quadratic vs exponential What is the difference between model and semi modals
What is the difference between model and semi modals Practice 8-8 exponential growth and decay
Practice 8-8 exponential growth and decay Exponential decay model
Exponential decay model 7-1 exploring exponential models form g
7-1 exploring exponential models form g 7-1 exploring exponential models
7-1 exploring exponential models Exploring exponential models practice
Exploring exponential models practice Using recursion in models and decision making
Using recursion in models and decision making Using functions in models and decision making
Using functions in models and decision making Exponential differentiation
Exponential differentiation