5 2 Inequalities and Triangles Definition of Inequality

5 -2 Inequalities and Triangles Definition of Inequality For any real numbers a and b, a > b if and only if there is a positive number c such that a=b+c

Review of the Symbols = > < Not equal to Greater than or equal to Less than or equal to Not greater than or equal to Not less than or equal to

Review of the Properties Comparison Property: a < b, a = b, or a > b Transitive Property: n n If a < b and b < c, then a < c If a > b and b > c, then a > c Addition and Subtraction Properties n n If a > b, then a + c > b + c, and a – c > b – c If a < b, then a + c < b + c, and a – c < b – c Multiplication and Division Properties n n If c > 0, and a < b, then ac < bc and a/c < b/c If c > 0, and a > b, then ac > bc and a/c > b/c If c < 0, and a < b, then ac > bc and a/c > b/c If c < 0, and a > b, then ac < bc and a/c < bc

Exterior Angle Review Exterior angle – forms a linear pair with one of the angles of a triangle. Example: 2 & 6… 2 & 5 5 4 1 9 2 Remote interior angles – the two angles that do NOT form a linear pair with the exterior angle. Example: 5 with 1 & 3 6 3 8 7

Theorem 5. 8 Exterior Angle Inequality Theorem – If an angle is an exterior angle of a triangle, then its measure is greater than the measure of either of its corresponding remote interior angles. 1 2 82° 3 Name two angles in ΔCDE that have a measure less than 82°. 2 and 3 Try #2 Check your Progress on page 282 5 and 6

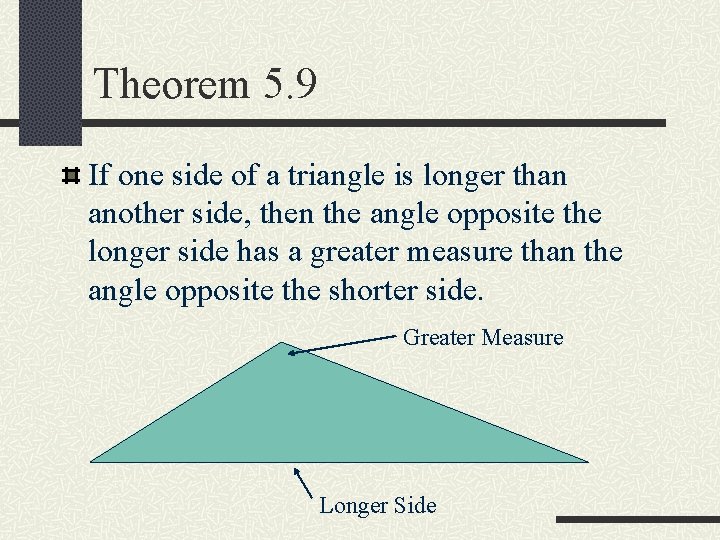
Theorem 5. 9 If one side of a triangle is longer than another side, then the angle opposite the longer side has a greater measure than the angle opposite the shorter side. Greater Measure Longer Side

Theorem 5. 10 If one angle of a triangle has a greater measure than another angle, then the side opposite the greater angle is longer than the side opposite the lesser angle. Greater Measure Longer Side

Try these – page 284 #1 -9 Homework #32 P. 285 11 -16, 18 -36 (x 3’s), 40 -42, 50, 52