5 2 Functions Tables and Graphs Vocabulary function

5 -2 Functions, Tables, and Graphs Vocabulary function input output

5 -2 Functions, Tables, and Graphs Rube Goldberg, a famous cartoonist, invented machines that perform ordinary tasks in extraordinary ways. Each machine operates according to a rule, or a set of steps, to produce a particular output. In mathematics, a function operates according to a rule to produce exactly one output value for each input value. The input is the value substituted into the function. The output is the value that results from the substitution of a given input into the function.

5 -2 Functions, Tables, and Graphs A function can be represented as a rule written in words, such as “double the number and add nine to the result, ” or by an equation with two variables. One variable represents the input, and the other represents the output. Function Rule Output variable Input variable You can use a table to organize and display the input and output values of a function.

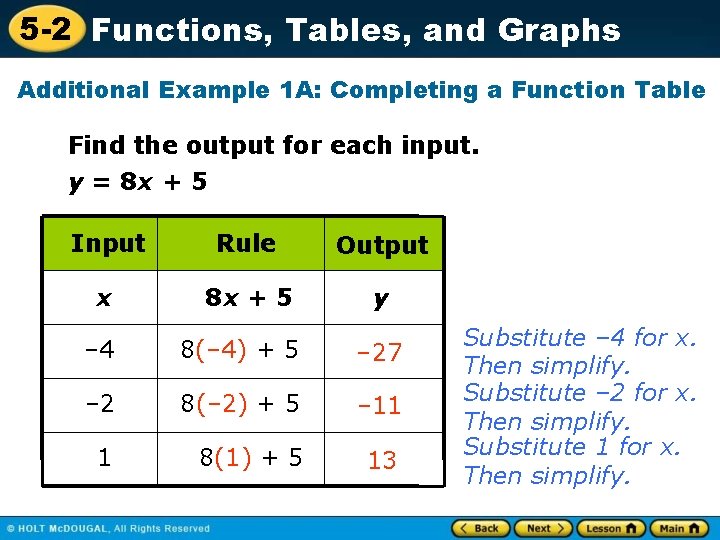
5 -2 Functions, Tables, and Graphs Additional Example 1 A: Completing a Function Table Find the output for each input. y = 8 x + 5 Input Rule Output x 8 x + 5 y – 4 8(– 4) + 5 – 27 – 2 8(– 2) + 5 – 11 1 8(1) + 5 13 Substitute – 4 for x. Then simplify. Substitute – 2 for x. Then simplify. Substitute 1 for x. Then simplify.

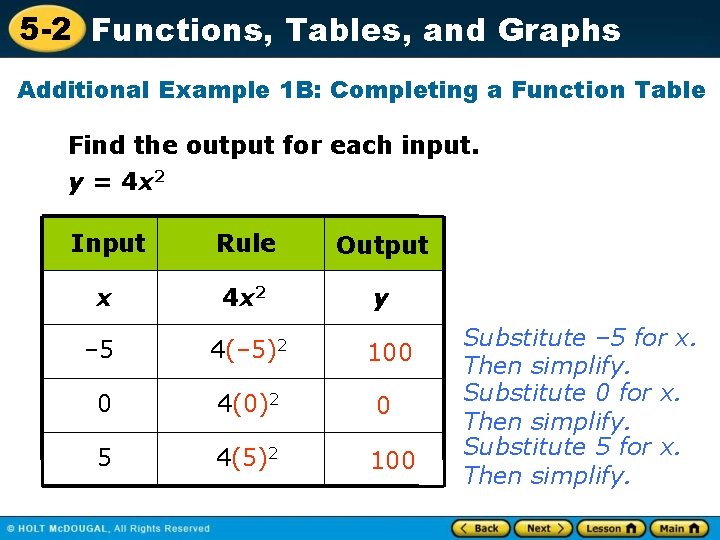
5 -2 Functions, Tables, and Graphs Additional Example 1 B: Completing a Function Table Find the output for each input. y = 4 x 2 Input Rule Output x 4 x 2 y – 5 4(– 5)2 100 0 4(0)2 0 5 4(5)2 100 Substitute – 5 for x. Then simplify. Substitute 0 for x. Then simplify. Substitute 5 for x. Then simplify.

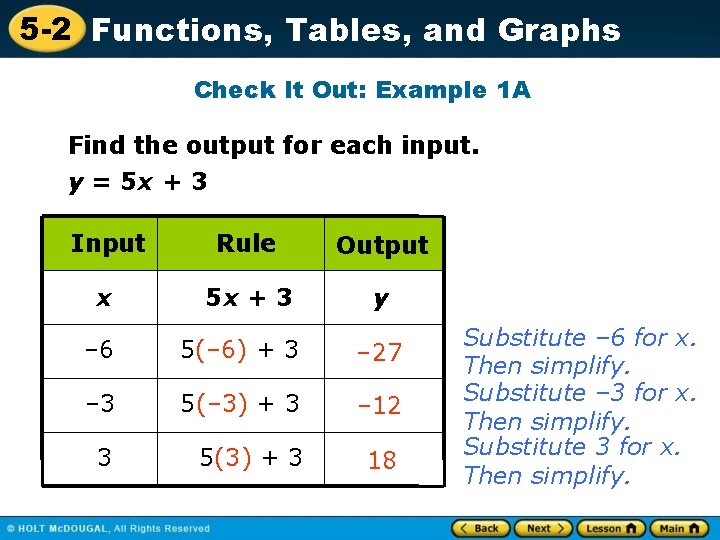
5 -2 Functions, Tables, and Graphs Check It Out: Example 1 A Find the output for each input. y = 5 x + 3 Input Rule Output x 5 x + 3 y – 6 5(– 6) + 3 – 27 – 3 5(– 3) + 3 – 12 3 5(3) + 3 18 Substitute – 6 for x. Then simplify. Substitute – 3 for x. Then simplify. Substitute 3 for x. Then simplify.

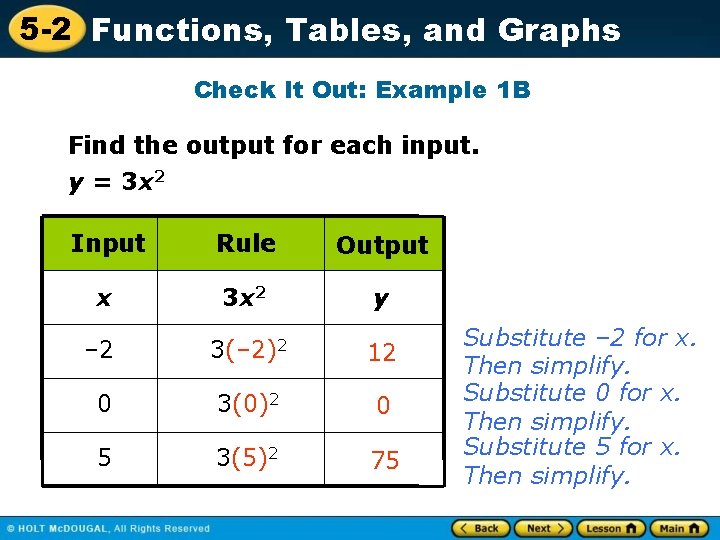
5 -2 Functions, Tables, and Graphs Check It Out: Example 1 B Find the output for each input. y = 3 x 2 Input Rule Output x 3 x 2 y – 2 3(– 2)2 12 0 3(0)2 0 5 3(5)2 75 Substitute – 2 for x. Then simplify. Substitute 0 for x. Then simplify. Substitute 5 for x. Then simplify.

5 -2 Functions, Tables, and Graphs You can also use a graph to represent a function. The corresponding input and output values together form unique ordered pairs. Remember! An ordered pair is a pair of numbers that represents a point on a graph.

5 -2 Functions, Tables, and Graphs Helpful Hint When writing an ordered pair, write the input value first and then the output value.

5 -2 Functions, Tables, and Graphs Additional Example 2 A: Graphing Functions Using Ordered Pairs Make a function table for x = – 2, – 1, 0, 1, and 2, and graph the resulting ordered pairs. 4 y = 3 x – 4 Input x Rule 3 x – 4 Output Ordered Pair y (x, y) – 2 3(– 2) – 4 – 10 (– 2, – 10) – 1 3(– 1) – 4 – 7 (– 1, – 7) 0 3(0) – 4 (0, – 4) 1 3(1) – 4 – 1 (1, – 1) 2 3(2) – 4 2 (2, 2) 2 – 4 – 2 (0, – 4) – 4 – 6 (– 1, – 7) – 8 (– 2, – 10) – 10 y (2, 2) 2 4 (1, – 1) x

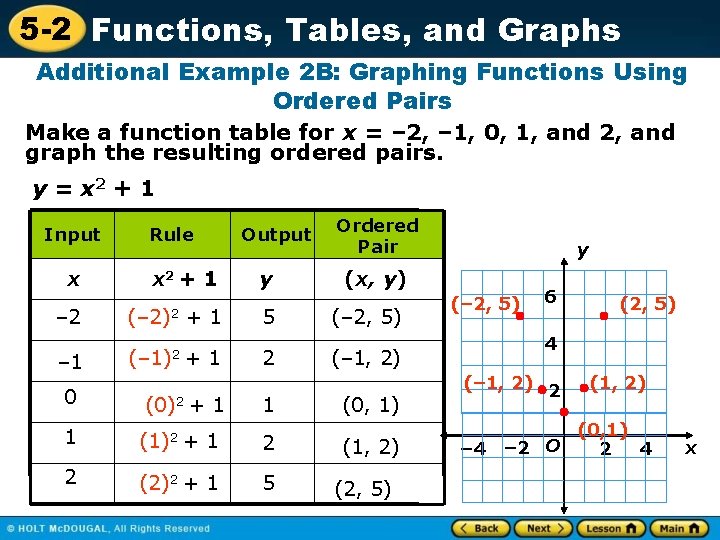
5 -2 Functions, Tables, and Graphs Additional Example 2 B: Graphing Functions Using Ordered Pairs Make a function table for x = – 2, – 1, 0, 1, and 2, and graph the resulting ordered pairs. y = x 2 + 1 Input x Rule x 2 + 1 – 2 (– 2)2 + 1 – 1 (– 1)2 +1 Output y 5 2 0 (0)2 + 1 1 (1)2 +1 2 2 (2)2 + 1 5 1 Ordered Pair y (x, y) (– 2, 5) (1, 2) (2, 5) 4 (– 1, 2) (0, 1) 6 (– 1, 2) 2 – 4 (1, 2) (0, 1) – 2 O 2 4 x

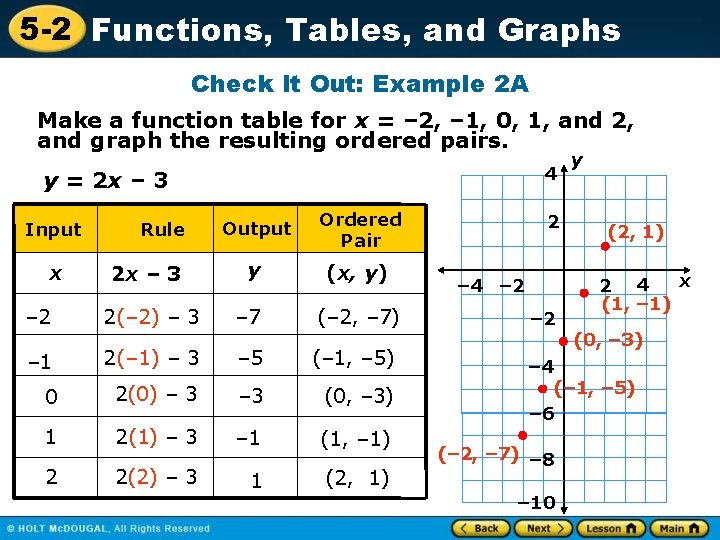
5 -2 Functions, Tables, and Graphs Check It Out: Example 2 A Make a function table for x = – 2, – 1, 0, 1, and 2, and graph the resulting ordered pairs. 4 y = 2 x – 3 Output Ordered Pair 2 x – 3 y (x, y) – 2 2(– 2) – 3 – 7 (– 2, – 7) – 1 2(– 1) – 3 – 5 (– 1, – 5) 0 2(0) – 3 (0, – 3) 1 2(1) – 3 – 1 (1, – 1) 2 2(2) – 3 1 (2, 1) Input x Rule 2 – 4 – 2 y (2, 1) x 2 4 (1, – 1) (0, – 3) – 4 (– 1, – 5) – 6 (– 2, – 7) – 8 – 10

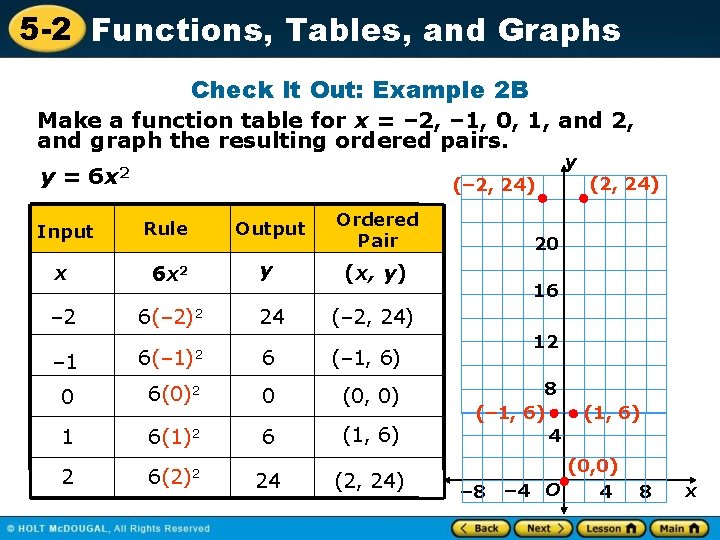
5 -2 Functions, Tables, and Graphs Check It Out: Example 2 B Make a function table for x = – 2, – 1, 0, 1, and 2, and graph the resulting ordered pairs. y= y 6 x 2 (– 2, 24) Input Rule Output Ordered Pair x 6 x 2 y (x, y) – 2 6(– 2)2 – 1 6(– 1)2 6 (– 1, 6) 0 6(0)2 0 (0, 0) 1 6(1)2 6 (1, 6) 2 6(2)2 24 24 (2, 24) 20 16 (– 2, 24) (2, 24) 12 8 (– 1, 6) 4 – 8 (1, 6) (0, 0) – 4 O 4 8 x

5 -2 Functions, Tables, and Graphs Lesson Quiz: Part I 1. Find the output for each input value. Input Rule Output x 4 x – 1 y – 2 4(– 2) – 1 – 9 0 4(0) – 1 4 4(4) – 1 15

5 -2 Functions, Tables, and Graphs Lesson Quiz: Part II 2. Make a function table with three input values for y = x 2 – 1, and graph the resulting ordered pairs. y Possible answer: Input x Rule x 2 – 1 – 22 – 1 0 2 Output Ordered Pair y (– 2, 3) 4 (2, 3) 2 (x, y) 3 (– 2, 3) 02 – 1 (0, – 1) 22 – 1 3 (2, 3) x – 4 – 2 – 4 2 4 (0, – 1)