5 2 Definite Integrals Sigma Notation What does

5. 2 Definite Integrals

Sigma Notation � What does the following notation mean? means the sum of the numbers from the lower number to the top number.

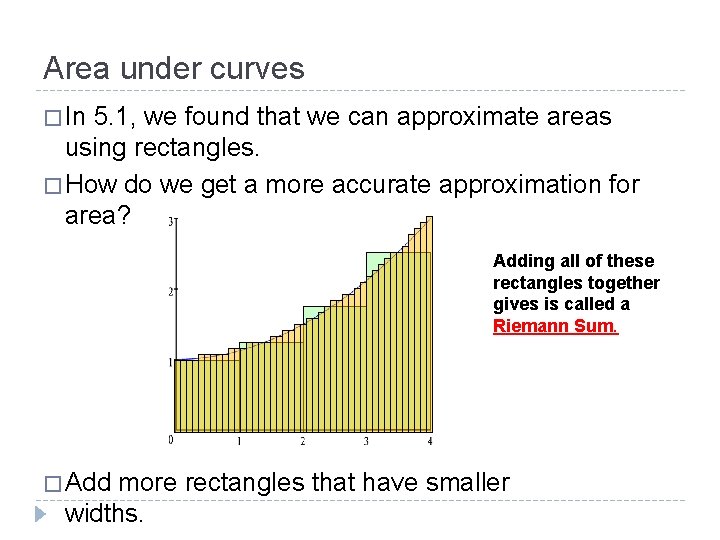
Area under curves � In 5. 1, we found that we can approximate areas using rectangles. � How do we get a more accurate approximation for area? Adding all of these rectangles together gives is called a Riemann Sum. � Add more rectangles that have smaller widths.

Definition of a Riemann Sum � Now imagine any function f that is defined on an interval [a, b]. � Let the notation xi’s points be on [a, b] such that x 0 = a, xn = b, and a < x 1 < x 2 < x 3 < … < xn-1 < b. � The points a, x 1, x 2, x 3, … , xn-1, xn+1, b form a partion of f notated as Δ on [a, b]. � Let Δxi be the width of the ith interval [xi-1, xi] and ci be any point in the ith interval. � Then, the Riemann sum of f for the partition is

Definition of a Definite Integral � As you add more and more rectangles under a curve, the widths, or partitions, of each rectangle become smaller and smaller. � SOUND � This FAMILIAR? ? causes the area to be more and more accurate…so accurate that it gives the actual area. � If f is continuous on [a, b] and [a, b] is partitioned into n subintervals of equation length Δx = (b – a)/n, then the definite integral of f over [a, b] is given by

Existence of Definite Integrals � All continuous functions are integrable. � That is, if a function f is continuous on an interval [a, b], then its definite integral over [a, b] exists. � These integrals calculate the area under a curve.

Leibniz’s is a Genius!!!! (thank goodness) � Leibniz introduced a notation for the definite integral that is much friendlier. Riemann’s notation Leibniz’s notation

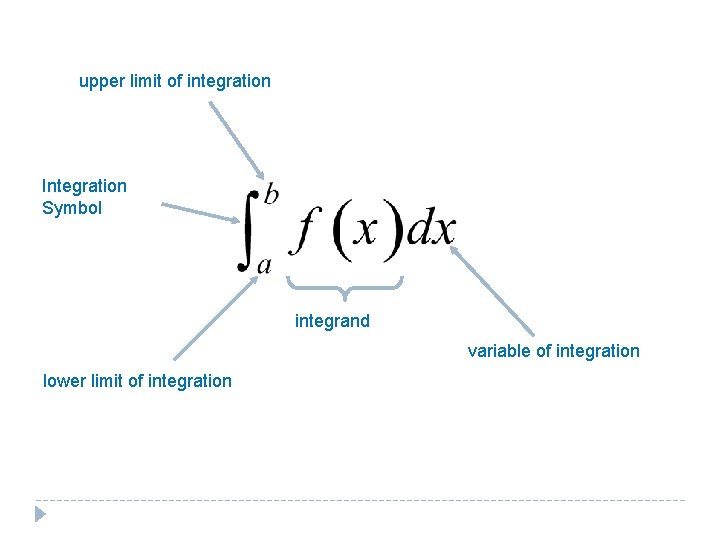
upper limit of integration Integration Symbol integrand variable of integration lower limit of integration

Areas under Curves � If an integrable function f(x) is nonpositive, the nonzero terms in the Riemann sums for f over an interval [a, b] are negatives of rectangle areas. � The integral of f from a to b is therefore the negative area of the region between the graph and the x-axis. � If f is nonpositive, then Area =

Areas under Curves � If an integrable function f(x) has both positive and negative values on an interval [a, b], then the Riemann sums for f on [a, b] add areas that lie above the x-axis to the negatives of areas that lie below the x-axis. � The resulting cancellations mean that the limiting value (integral) is a number whose magnitude is less than the total area between the curve and the x-axis. � Therefore, for any integrable function,

Your Best Friend…fn. Int � We will eventually learn how to evaluate some definite integrals by hand. However, not all definite integrals can be evaluated by hand (at least, not without the help of some geniuses who have done them first). � Your calculator has a function in it that will evaluate a definite integral, which finds the area under a curve. � fn. Int (MATH, #9) � Syntax: � (old operating system): fn. Int(f(x), x, a, b) � (new operating system):

fn. Int � Use fn. Int to find the following integrals: