5 2 Congruent Polygons Identifying and Using Corresponding

5. 2 Congruent Polygons

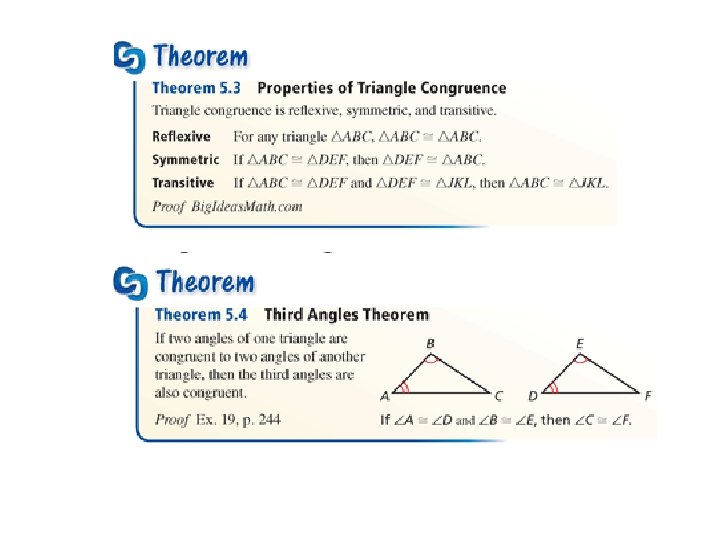
Identifying and Using Corresponding Parts A rigid motion maps each part of a figure to a corresponding part of its image. Because rigid motions preserve length and angle measure, corresponding parts of congruent figures are congruent. When ∆DEF is an image of ∆ABC after a rigid motion or a composition of rigid motions, you can write congruence statements for the corresponding angles and corresponding sides.

When you write a congruence statement for two polygons, always list the corresponding vertices in the same order. Possible congruence statement for the above triangles could be: ∆ABC = ∆DEF ∆BCA = ∆EFD

Example 1: Identifying Corresponding Parts Write a congruence statement for the triangles. Identify all pairs of congruent corresponding parts.

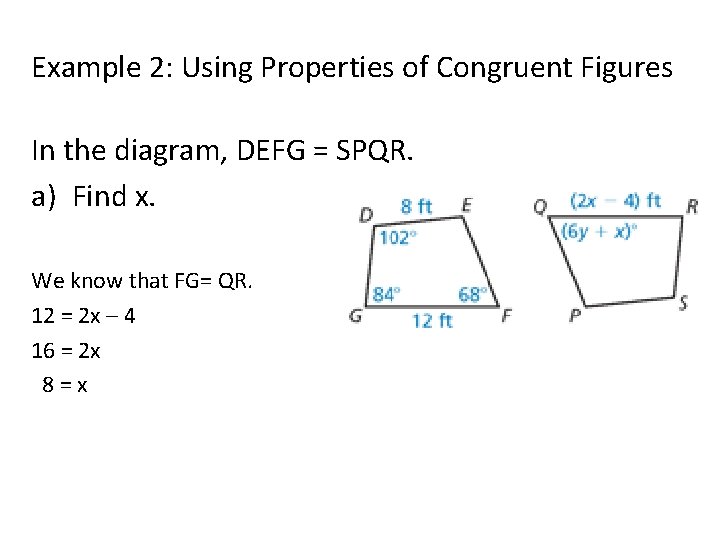
Example 2: Using Properties of Congruent Figures In the diagram, DEFG = SPQR. a) Find x. We know that FG= QR. 12 = 2 x – 4 16 = 2 x 8=x

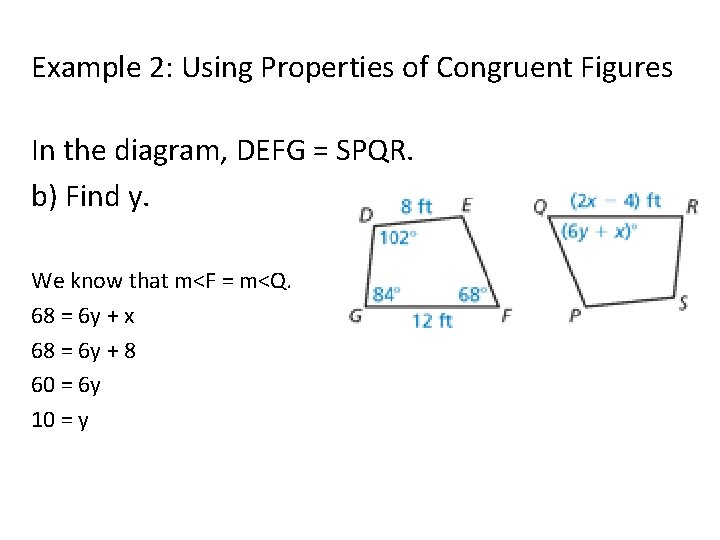
Example 2: Using Properties of Congruent Figures In the diagram, DEFG = SPQR. b) Find y. We know that m<F = m<Q. 68 = 6 y + x 68 = 6 y + 8 60 = 6 y 10 = y

Example 3: Showing that Figures are Congruent You divide a wall into orange and blue sections along segment JK. Will the sections of the wall be the same shape and size? Explain. From the diagram, <A = <C and <D = <B, since all right triangles are congruent. By the Lines Perpendicular to a Transversal Theorem, segment AB is parallel to segment DC. <1 = <4 and <2 = <3 because of Alternate Interior Angles Theorem. So, all pairs of corresponding angles are congruent. The diagram shows AJ = CK, DK = BJ and AD = CB. By the Reflexive Property of Congruency JK = KJ. So, all pairs of corresponding sides are congruent. Because all corresponding parts are congruent, AJKD = CKJB.

You try! In the diagram ABGH = CDEF. 1) Identify all pairs of congruent corresponding parts. <A = <C AB = CD <B = <D <H = <F <G = <E AH = CF HG = FE GB = ED 2) Find the value of x. 4 x + 5 = 105 4 x = 100 x = 25

You try! 3) In the diagram, show that ∆PTS = ∆RTQ. Since segment PS is parallel to segment RQ, <P= <R because of Alternate Interior Angles Theorem(transversal being PR) and <S = <Q because of Alternate Interior Angles Theorem (transversal being SQ). <T = <T because of Reflexive Property of Congruence. The diagram shows that each side is congruent to its corresponding side. So, since all corresponding parts are congruent ∆PTS = ∆RTQ.

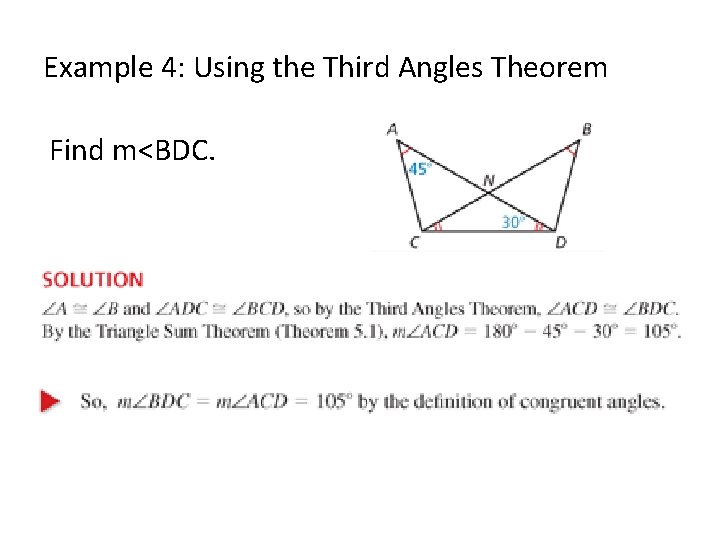
Example 4: Using the Third Angles Theorem Find m<BDC.

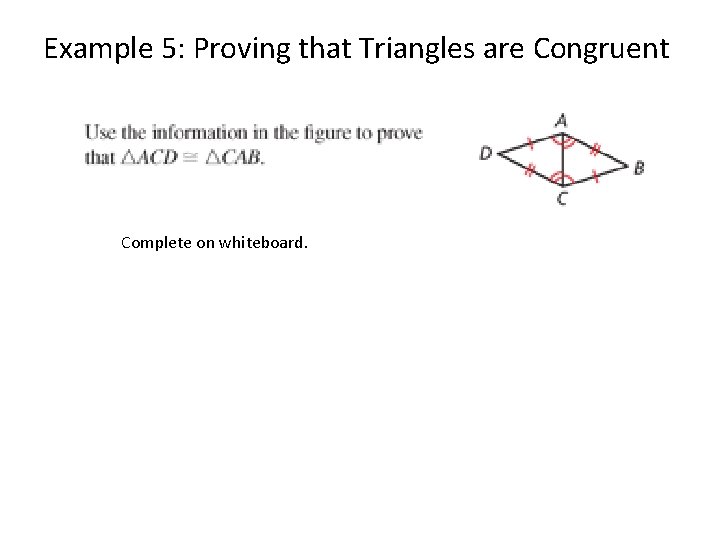
Example 5: Proving that Triangles are Congruent Complete on whiteboard.