5 1 Solving Systems of Linear Equations by

5. 1 Solving Systems of Linear Equations by Graphing

System of Linear Equations A set of two or more linear equations in the same variables Example: x+y=7 Equation 1 2 x – 3 y = -11 Equation 2 Solution of a system of Linear Equations In two variables, is an ordered pair that is the solution to each equation in the system

Example 1: Checking Solutions Tell whether the ordered pair is a solution of the system of linear equations. a) (2, 5); x + y = 7 2 x – 3 y = -11 Equation 2 Substitute 2 in for x and 5 in for y in each equation. Equation 1 x+y=7 2+5=7 7=7 Equation 2 2 x – 3 y = -11 2(2) – 3(5) = -11 4 – 15 = -11 Since the ordered pair (2, 5) is a solution of each of the equations, it is a solution to the of the linear system.

Example 1: Checking Solutions Tell whether the ordered pair is a solution of the system of linear equations. b) (-2, 0); y = -2 x – 4 y=x+4 Equation 1 Equation 2 Substitute -2 in for x and 0 in for y in each equation. Equation 1 y = -2 x - 4 0 = -2(-2) - 4 0=4 -4 0=0 Equation 2 y=x+4 0 = -2 + 4 0=2 Since the ordered pair (-2, 0) is not a solution of each of the equations, it is NOT a solution to the of the linear

You try! Tell whether the ordered pair is a solution to the system of linear equations. 1) (1, -2); 2 x + y = 0 -x + 2 y = 5 2) (1, 4); y = 3 x + 1 y = -x + 5 Equation 1 2(1) + (-2) = 0 2 + (-2) = 0 0=0 Equation 1 4 = 3(1) + 1 4=3+1 4=4 Equation 2 -(1) + 2(-2) = 5 -1 + (-4) = 5 -5 = 5 Equation 2 4 = -(1) + 5 4 = -1 + 5 4=4 (1, -2) is not a solution to the system of linear equations. (1, 4) is a solution to the system of linear equations.

Solving Systems of Linear Equations by Graphing Step 1: Graph each equation in the same coordinate plane. Step 2: Estimate the point of intersection. Step 3: Check the point from step 2 by substituting for x and y in each equation of the original system.

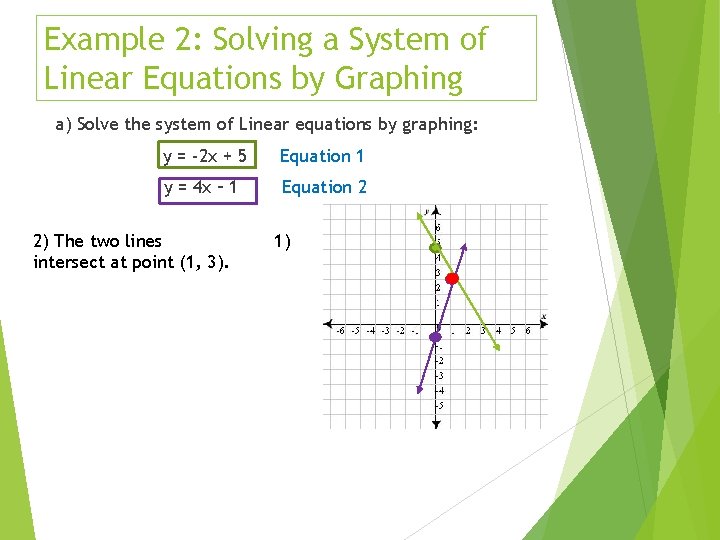
Example 2: Solving a System of Linear Equations by Graphing a) Solve the system of Linear equations by graphing: y = -2 x + 5 Equation 1 y = 4 x – 1 Equation 2 2) The two lines intersect at point (1, 3). 1)

3) Check your work: y = -2 x + 5 3 = -2(1) + 5 3=3 Equation 1 y = 4 x – 1 Equation 2 3 = 4(1) – 1 3=3 (1, 3) is the solution to the system.

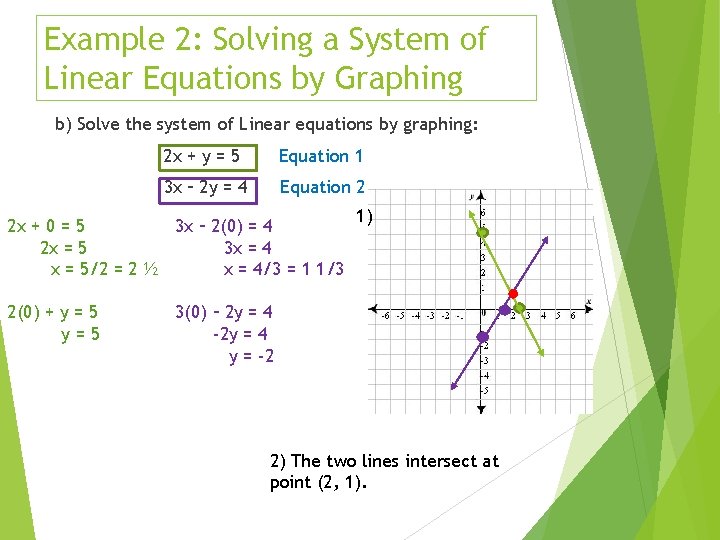
Example 2: Solving a System of Linear Equations by Graphing b) Solve the system of Linear equations by graphing: 2 x + y = 5 Equation 1 3 x – 2 y = 4 Equation 2 2 x + 0 = 5 3 x – 2(0) = 4 2 x = 5 3 x = 4 x = 5/2 = 2 ½ x = 4/3 = 1 1/3 2(0) + y = 5 y=5 1) 3(0) – 2 y = 4 -2 y = 4 y = -2 2) The two lines intersect at point (2, 1).

3) Check your work: 2 x + y = 5 2(2) + 1 = 5 5=5 Equation 1 3 x – 2 y = 4 Equation 2 3(2) – 2(1) = 4 6– 2=4 4=4 (2, 1) is the solution to the system.

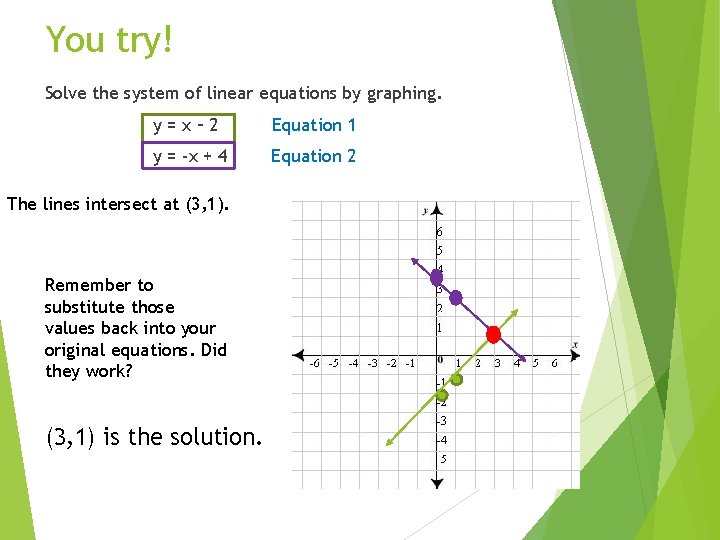
You try! Solve the system of linear equations by graphing. y=x– 2 Equation 1 y = -x + 4 Equation 2 The lines intersect at (3, 1). Remember to substitute those values back into your original equations. Did they work? (3, 1) is the solution.

Example 3: Solving Real-Life Problems Let x be the price (in dollars) per bundle. Let y be the price (in dollars) per roll.

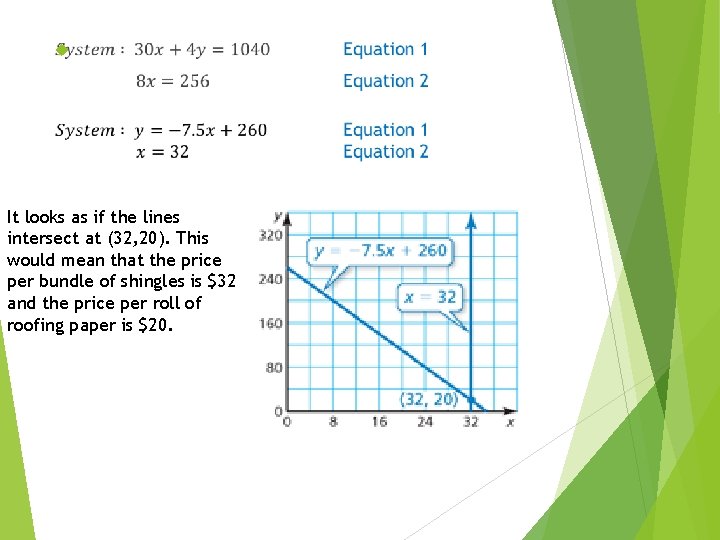
It looks as if the lines intersect at (32, 20). This would mean that the price per bundle of shingles is $32 and the price per roll of roofing paper is $20.

Remember you can check your solution by substituting the x and y values into the original equations!! Equation 1 30 x + 4 y = 1040 30(32) + 4(20) = 1040 Equation 2 8 x = 256 8(32) = 256

You try! You have a total of 18 math and science exercises for homework. You have 6 more math exercises than science exercises. How many exercises do you have in each subject? Let x be the number of math exercises. Let y be the number of science exercises.

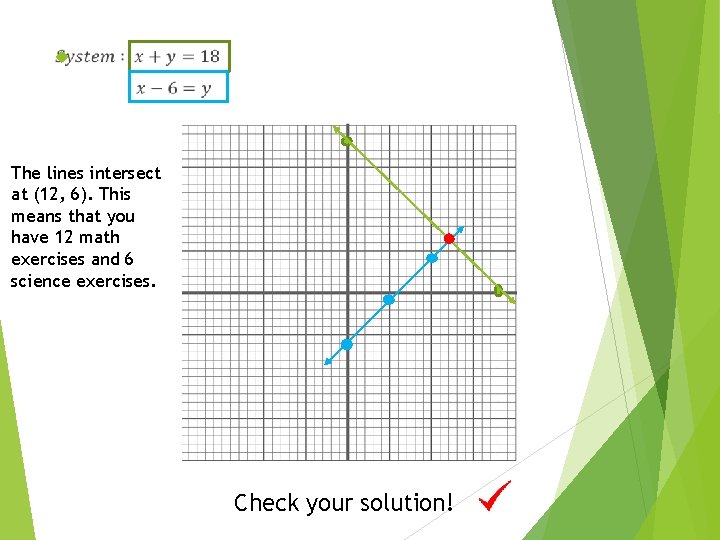
The lines intersect at (12, 6). This means that you have 12 math exercises and 6 science exercises. Check your solution!