5 1 Polynomial Functions Learning goals graph functions

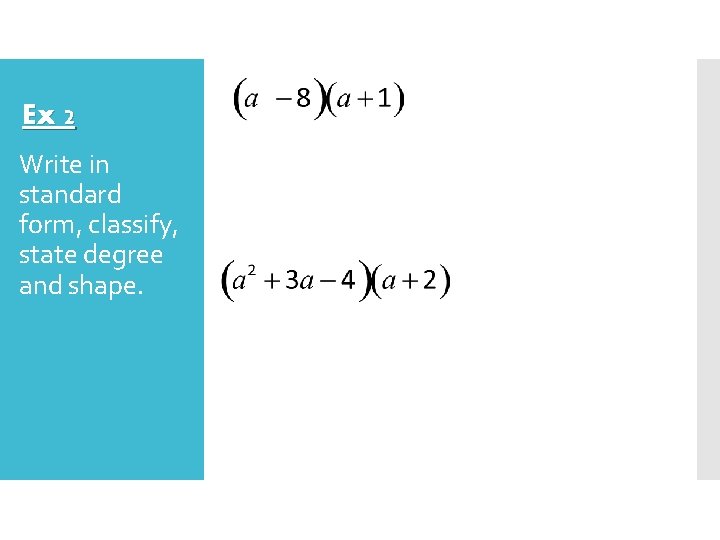
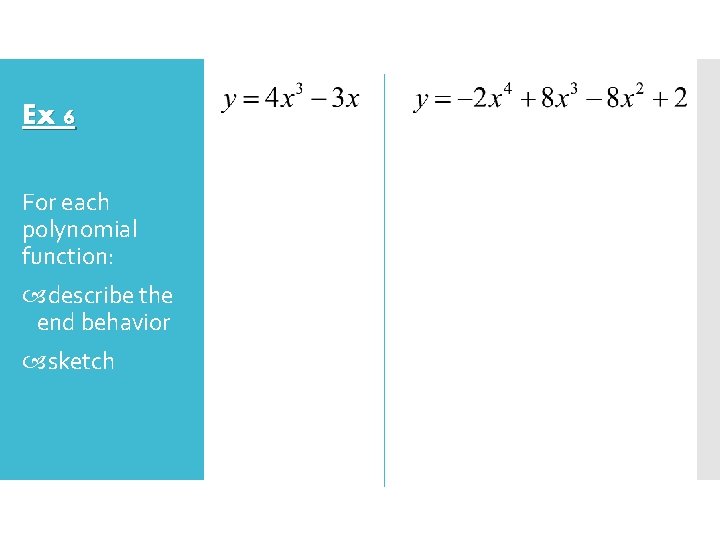
  • Slides: 13
Download presentation
5. 1 Polynomial Functions Learning goals • graph functions expressed symbolically and show key

5. 1 Polynomial Functions Learning goals • graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases. • graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior.

monomial : a number, a variable, or the product of a real number and

monomial : a number, a variable, or the product of a real number and variables with whole number exponents polynomial : a monomial or the sum of monomials Vocabulary degree : For a monomial – the sum of its exponents For a polynomial – the largest sum of exponents from a term **Always put answers in standard form: descending order of exponents

By # of Terms 1 – monomial 2 – binomial 3 – trinomial 4

By # of Terms 1 – monomial 2 – binomial 3 – trinomial 4 or more - polynomial Classifying Polynomials By Degree 0 – constant 1 – linear 2 – quadratic 3 – cubic 4 – quartic 5 – quintic Shape

Ex 1 Put in standard form What is the degree of the polynomial? Classify

Ex 1 Put in standard form What is the degree of the polynomial? Classify each polynomial by degree and number of terms What shape is it?

Ex 2 Write in standard form, classify, state degree and shape.

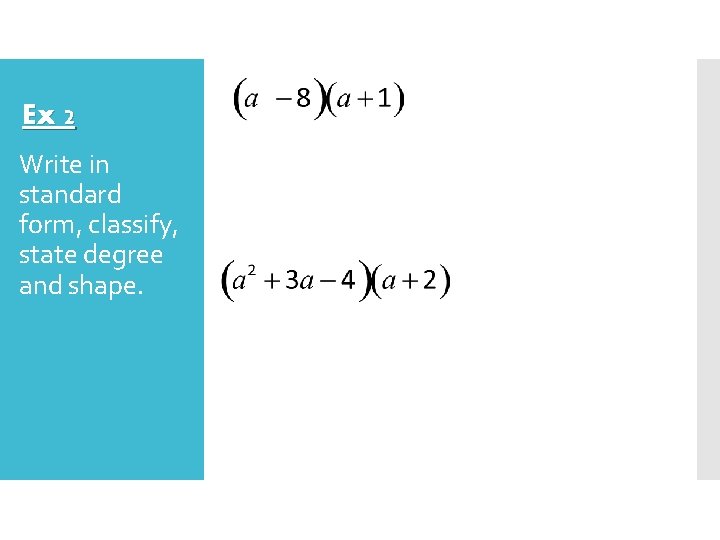
Ex 2 Write in standard form, classify, state degree and shape.

The degree of a polynomial function affects the shape of its graph the maximum

The degree of a polynomial function affects the shape of its graph the maximum number of turning points the way behaves at its ends Vocabulary turning point : places where a graph changes direction end behavior : direction of the graph where the arrows appear (far left and far right of the graph)

Vocabulary relative minimum /relative maximum peaks and valleys within the graph of a polynomial

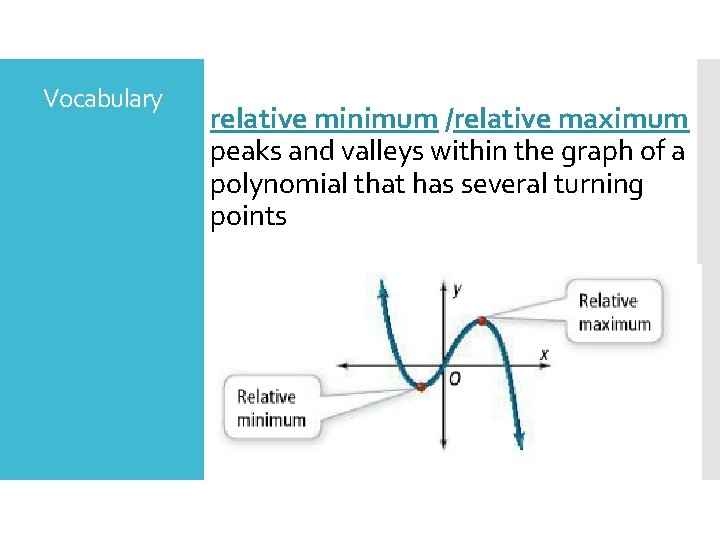
Vocabulary relative minimum /relative maximum peaks and valleys within the graph of a polynomial that has several turning points

Ex 3 Find the relative minimum and maximum

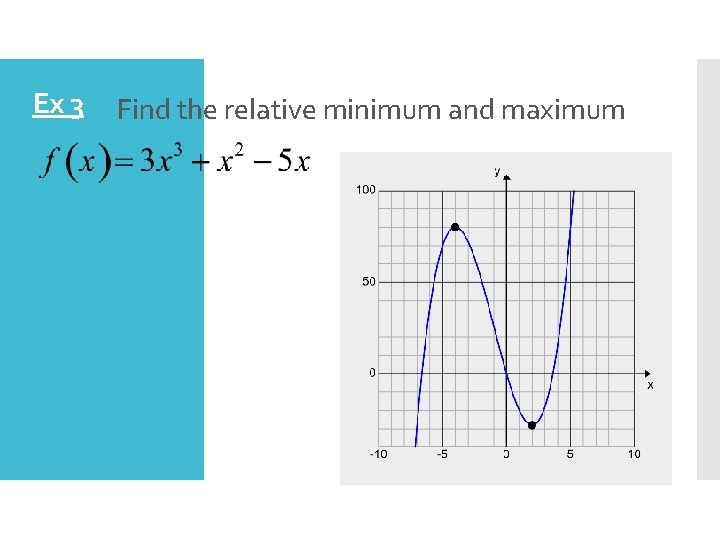
Ex 3 Find the relative minimum and maximum

End Behavior a a behaves is positive is negative like n is even up

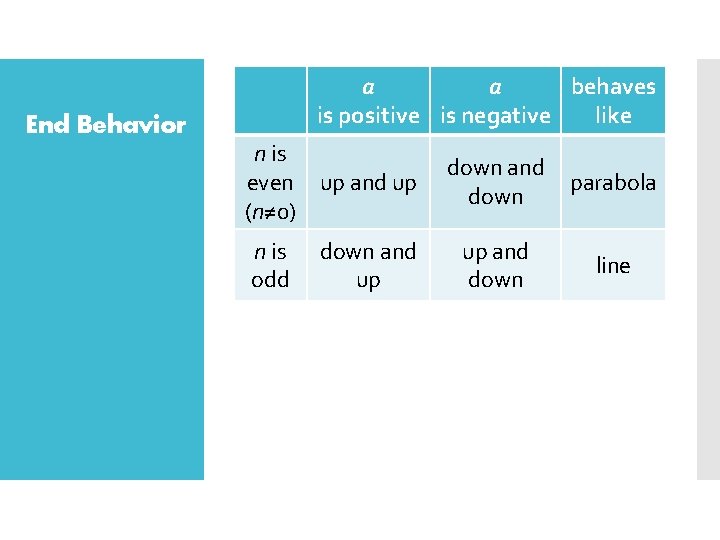
End Behavior a a behaves is positive is negative like n is even up and up (n≠ 0) n is odd down and up down and down parabola up and down line

Ex 4 Describe the end behavior Is the graph odd or even? Is the

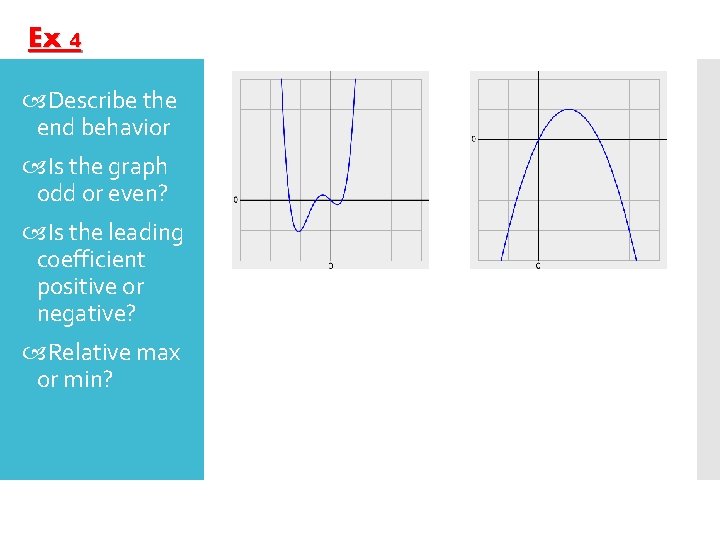
Ex 4 Describe the end behavior Is the graph odd or even? Is the leading coefficient positive or negative? Relative max or min?

Ex 5 Describe the end behavior Is the graph odd or even? Is the

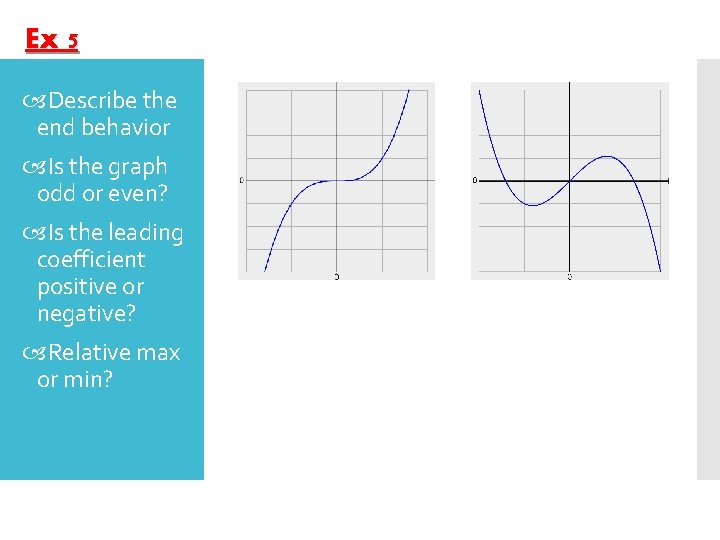
Ex 5 Describe the end behavior Is the graph odd or even? Is the leading coefficient positive or negative? Relative max or min?

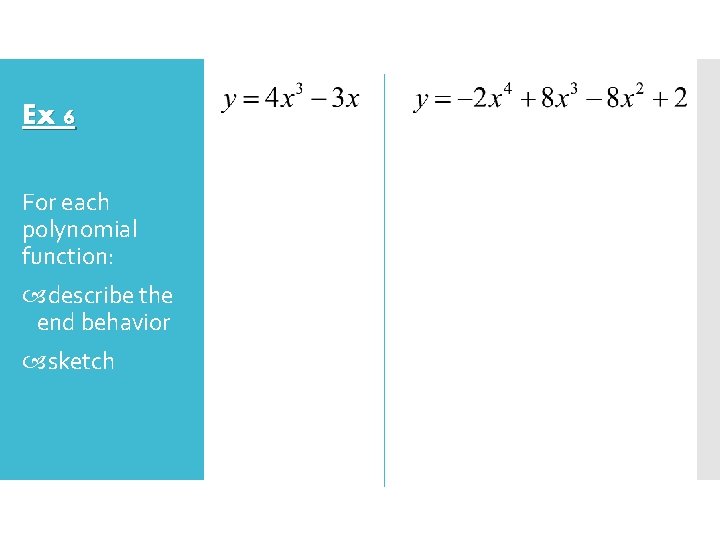
Ex 6 For each polynomial function: describe the end behavior sketch

Ex 6 For each polynomial function: describe the end behavior sketch

Ex 7 For each polynomial function: describe the end behavior sketch

Ex 7 For each polynomial function: describe the end behavior sketch