5 1 Modeling Data with Quadratic Functions 1


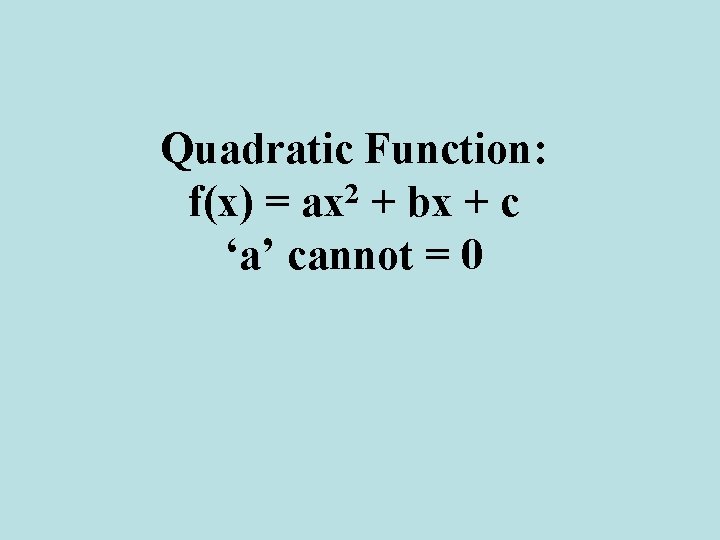








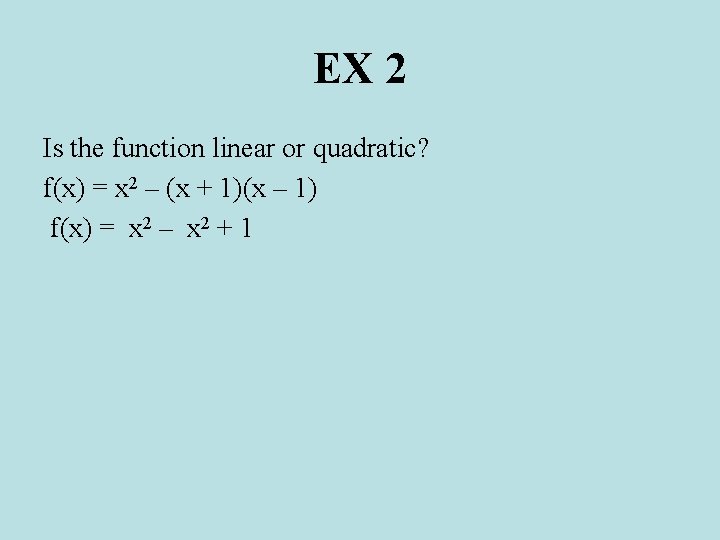
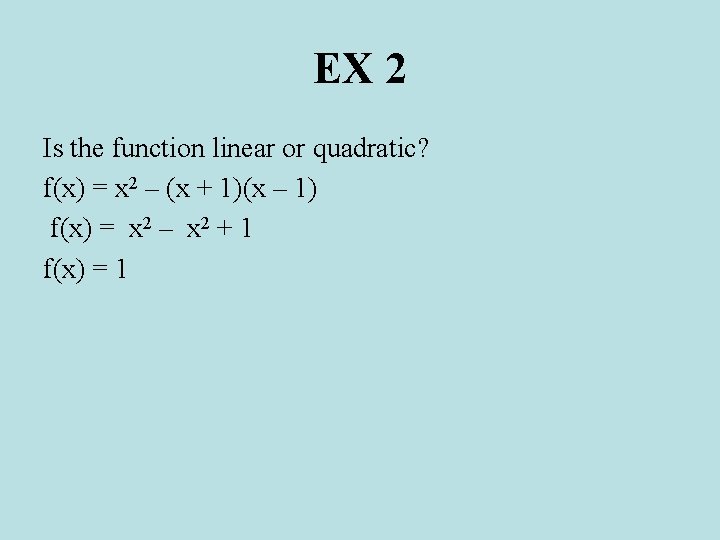












- Slides: 37

5. 1 Modeling Data with Quadratic Functions 1. Quadratic Functions and Their Graphs

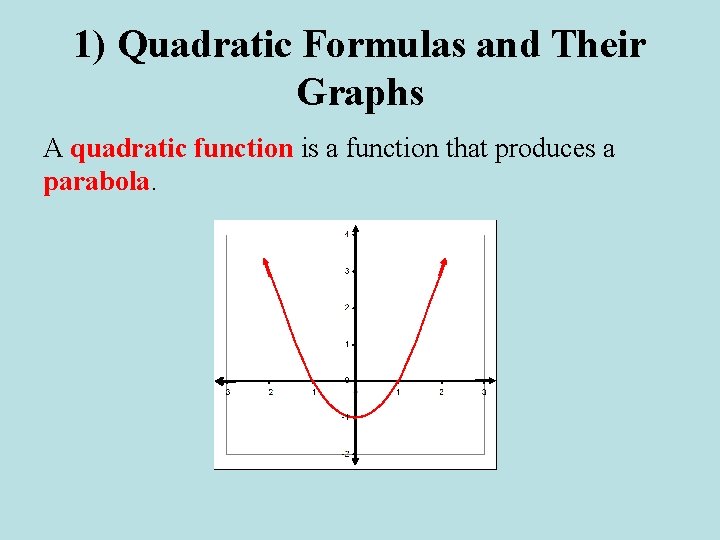
1) Quadratic Formulas and Their Graphs A quadratic function is a function that produces a parabola.

1) Quadratic Formulas and Their Graphs A quadratic function is a function that produces a parabola.

1) Quadratic Formulas and Their Graphs A quadratic function is a function that produces a parabola.

1) Quadratic Formulas and Their Graphs The equation of a quadratic function can be written in standard form. Quadratic term Linear term Constant term
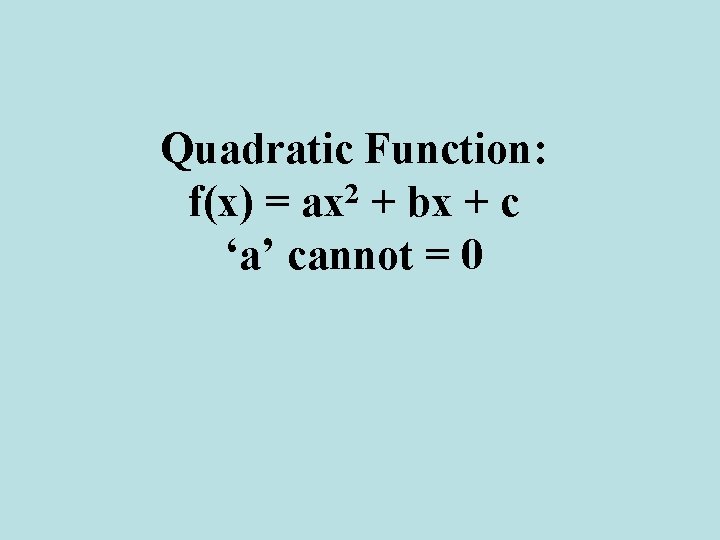
Quadratic Function: f(x) = ax 2 + bx + c ‘a’ cannot = 0

1) Quadratic Formulas and Their Graphs Since the largest exponent of function is 2, we say that a quadratic equation has a degree of 2. Equations of second degree are called quadratic.

QUADRATICS - - what are they? Y = ax² + bx + c FORM ____________ Quadratic term Linear term Important Details o c is y-intercept o a determines shape and position if a > 0, then opens up if a < 0, then opens down o Vertex: x-coordinate is at –b/2 a Constant

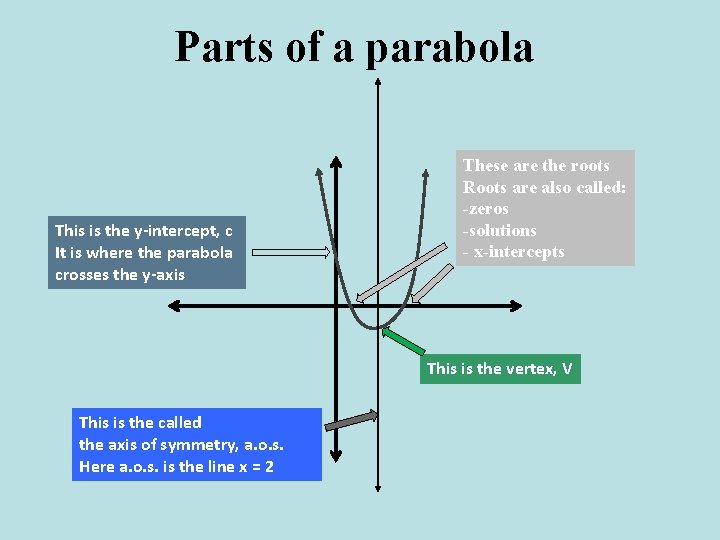
Parts of a parabola This is the y-intercept, c It is where the parabola crosses the y-axis These are the roots Roots are also called: -zeros -solutions - x-intercepts This is the vertex, V This is the called the axis of symmetry, a. o. s. Here a. o. s. is the line x = 2

STEPS FOR GRAPHING Y = ax² + bx +c 1 2 3 4 HAPPY or SAD ? VERTEX = ( -b / 2 a , f(-b / 2 a) ) T- Chart Axis of Symmetry

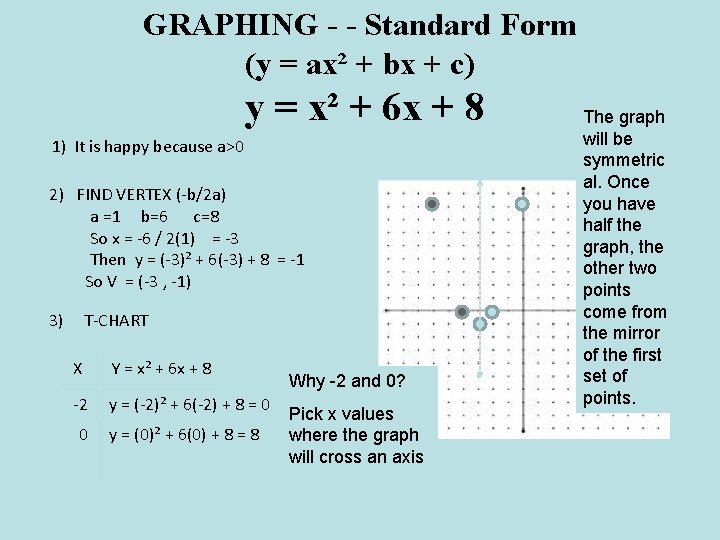
GRAPHING - - Standard Form (y = ax² + bx + c) y = x² + 6 x + 8 1) It is happy because a>0 2) FIND VERTEX (-b/2 a) a =1 b=6 c=8 So x = -6 / 2(1) = -3 Then y = (-3)² + 6(-3) + 8 = -1 So V = (-3 , -1) 3) T-CHART X Y = x² + 6 x + 8 -2 y = (-2)² + 6(-2) + 8 = 0 0 y = (0)² + 6(0) + 8 = 8 Why -2 and 0? Pick x values where the graph will cross an axis The graph will be symmetric al. Once you have half the graph, the other two points come from the mirror of the first set of points.

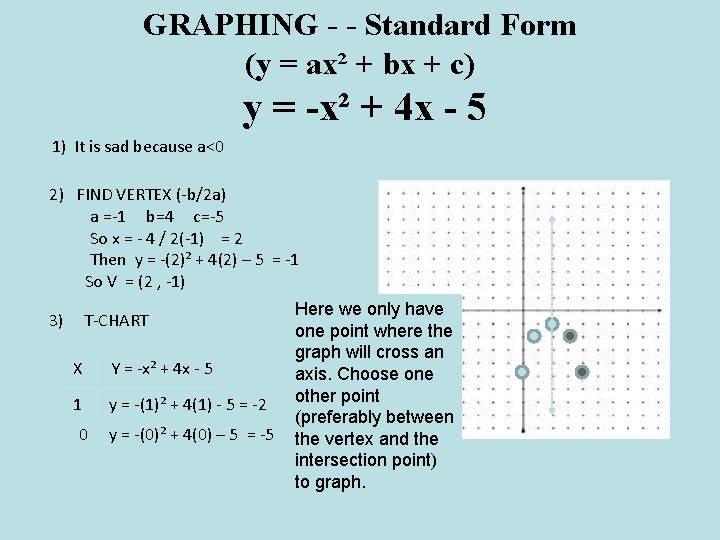
GRAPHING - - Standard Form (y = ax² + bx + c) y = -x² + 4 x - 5 1) It is sad because a<0 2) FIND VERTEX (-b/2 a) a =-1 b=4 c=-5 So x = - 4 / 2(-1) = 2 Then y = -(2)² + 4(2) – 5 = -1 So V = (2 , -1) 3) T-CHART X Y = -x² + 4 x - 5 1 y = -(1)² + 4(1) - 5 = -2 0 y = -(0)² + 4(0) – 5 = -5 Here we only have one point where the graph will cross an axis. Choose one other point (preferably between the vertex and the intersection point) to graph.

1) Quadratic Formulas and Their Graphs Example 1: Determine whether each function is linear or quadratic. Identify the quadratic term, linear term and constant term.

1) Quadratic Formulas and Their Graphs Example 1: Determine whether each function is linear or quadratic. Identify the quadratic term, linear term and constant term. This IS a quadratic function. QUADRATIC TERM: x 2 LINEAR TERM: 3 x CONSTANT TERM: none

1) Quadratic Formulas and Their Graphs Example 1: Determine whether each function is linear or quadratic. Identify the quadratic term, linear term and constant term. This IS a quadratic function. This is NOT a quadratic function. QUADRATIC TERM: x 2 QUADRATIC TERM: none LINEAR TERM: 3 x LINEAR TERM: 5 x CONSTANT TERM: none

Ex 1 Is the function linear or quadratic? f(x) = (2 x – 1)2 The function is quadratic because “a” (the coefficient of x squared) is equal to 4. If “a” were equal to zero, then the function would be linear.

EX 2 Is the function linear or quadratic? f(x) = x 2 – (x + 1)(x – 1)
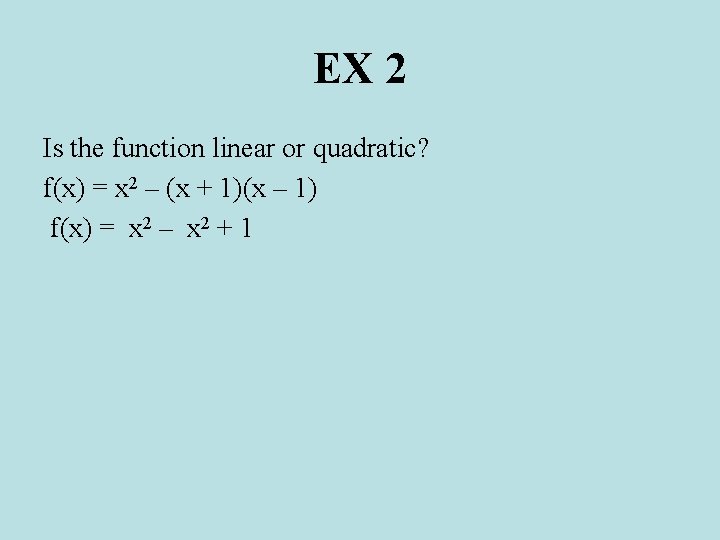
EX 2 Is the function linear or quadratic? f(x) = x 2 – (x + 1)(x – 1) f(x) = x 2 – x 2 + 1
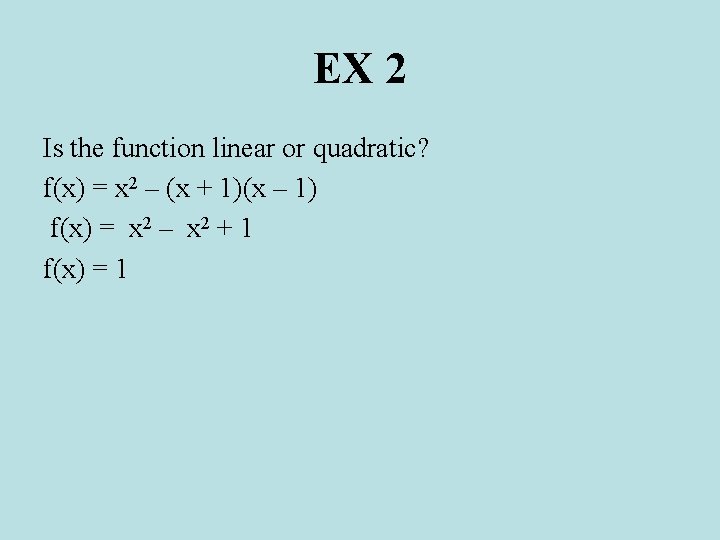
EX 2 Is the function linear or quadratic? f(x) = x 2 – (x + 1)(x – 1) f(x) = x 2 – x 2 + 1 f(x) = 1

EX 2 Is the function linear or quadratic? f(x) = x 2 – (x + 1)(x – 1) f(x) = x 2 – x 2 + 1 f(x) = 1 The function is linear.

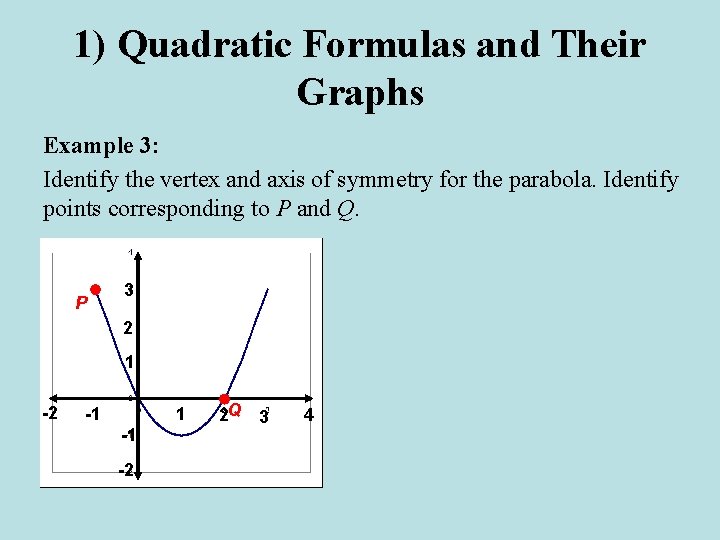
1) Quadratic Formulas and Their Graphs Example 3: Identify the vertex and axis of symmetry for the parabola. Identify points corresponding to P and Q. P 3 2 1 -2 -1 1 -1 -2 2 Q 3 4

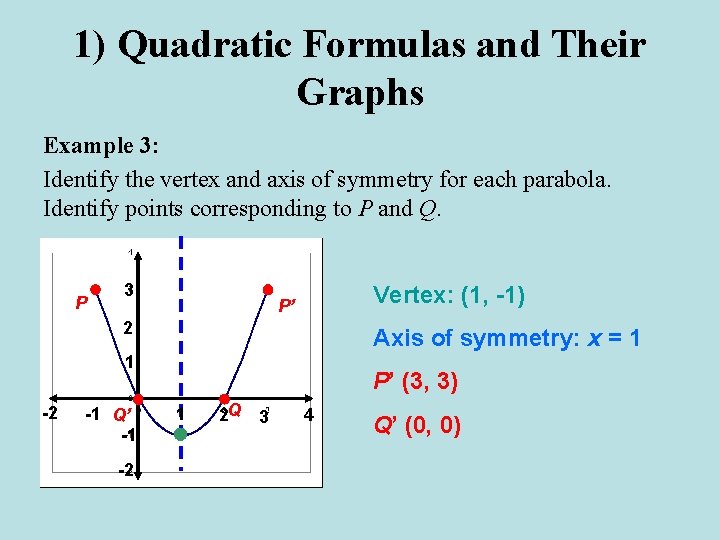
1) Quadratic Formulas and Their Graphs Example 3: Identify the vertex and axis of symmetry for each parabola. Identify points corresponding to P and Q. P 3 P Vertex: (1, -1) P’ 2 Axis of symmetry: x = 1 1 -2 -1 Q’ -1 -2 P’ (3, 3) 1 2 Q 3 4 Q’ (0, 0)

Ex 4 y = 2 x 2 + x – c contains the point (1, 2). Find c.

Ex 4 y = 2 x 2 + x – c contains the point (1, 2). Find c. 2 = 2(1)2 + 1 – c

Ex 4 y = 2 x 2 + x – c contains the point (1, 2). Find c. 2 = 2(1)2 + 1 – c 2=3–c

Ex 4 y = 2 x 2 + x – c contains the point (1, 2). Find c. 2 = 2(1)2 + 1 – c 2=3–c -1 = -c

Ex 4 y = 2 x 2 + x – c contains the point (1, 2). Find c. 2 = 2(1)2 + 1 – c 2=3–c -1 = -c c=1

1) Quadratic Formulas and Their Graphs We can graph parabolas using a table of values.

1) Quadratic Formulas and Their Graphs We can graph parabolas using a table of values. Recall…graphing linear functions…

1) Quadratic Formulas and Their Graphs Example 2: Graph the parent function f(x) = x 2 using a table of values.

1) Quadratic Formulas and Their Graphs Example 2: Graph the parent function f(x) = x 2 using a table of values. x -2 -1 0 1 2 y

1) Quadratic Formulas and Their Graphs Example 2: Graph the parent function f(x) = x 2 using a table of values. x y -2 (-2)2 = 4 -1 (-1)2 = 1 0 (0)2 = 0 1 (1)2 = 1 2 (2)2 = 4

1) Quadratic Formulas and Their Graphs Example 2: Graph the parent function f(x) = x 2 using a table of values. x y -2 4 -1 1 0 0 1 1 2 4

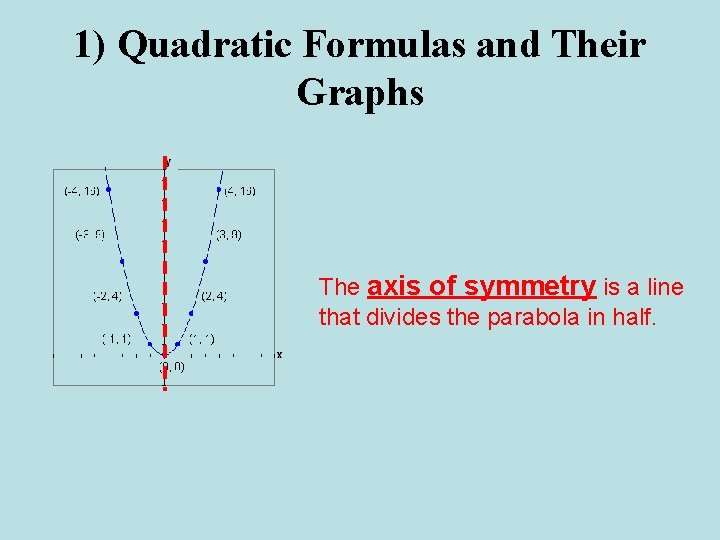
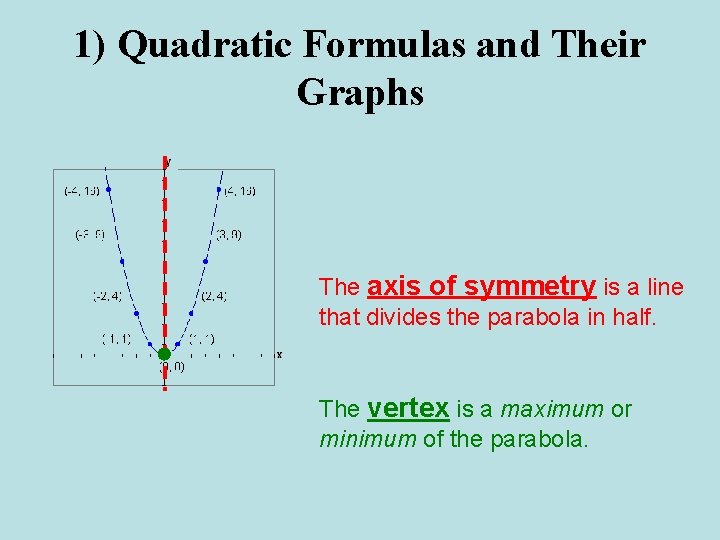
1) Quadratic Formulas and Their Graphs The axis of symmetry is a line that divides the parabola in half.

1) Quadratic Formulas and Their Graphs The axis of symmetry is a line that divides the parabola in half. The vertex is a maximum or minimum of the parabola.

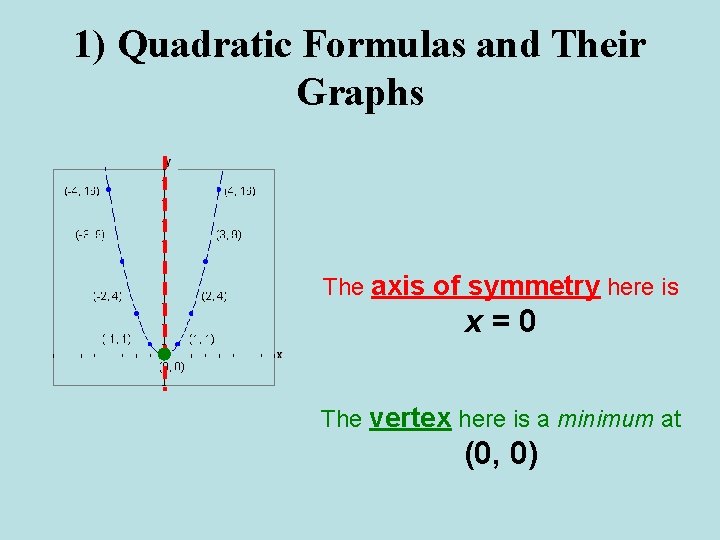
1) Quadratic Formulas and Their Graphs The axis of symmetry here is x=0 The vertex here is a minimum at (0, 0)

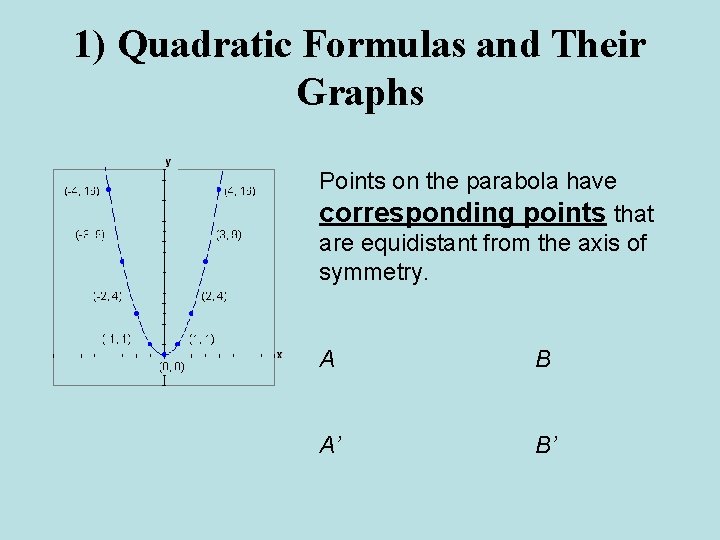
1) Quadratic Formulas and Their Graphs Points on the parabola have corresponding points that are equidistant from the axis of symmetry. A B A’ B’