5 1 Midsegments of Triangles Brett Solberg AHS

5. 1 Midsegments of Triangles Brett Solberg AHS ’ 11 -’ 12

Warm-up 11 -28 -2011 � 1) Find the distance between (1, 4) and (4, 8). � 2) Find the midpoint of the segment whose endpoints are (4, 11) and (6, 3). � 3) Find the slope of the line containing the points (8, 3) and (7, 12).

Today’s Agenda � Chapter 5 Relationships Within Triangles ◦ Triangle Midsegments � Test Make-up

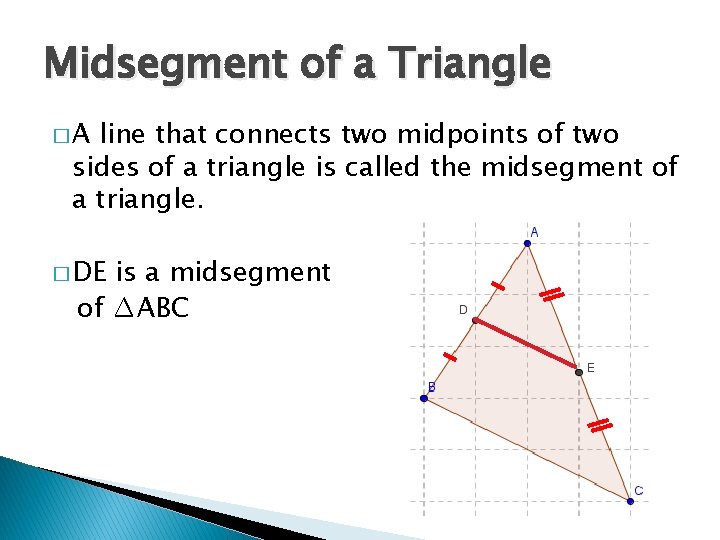
Midsegment of a Triangle �A line that connects two midpoints of two sides of a triangle is called the midsegment of a triangle. � DE is a midsegment of ∆ABC

Discovery � What relationships did you discover between a triangle midsegment and the third side of a triangle?

Triangle Midsegment Theorem � The midsegment of a triangle is half the length of the third side of a triangle. � DE = 5 � BC = 10

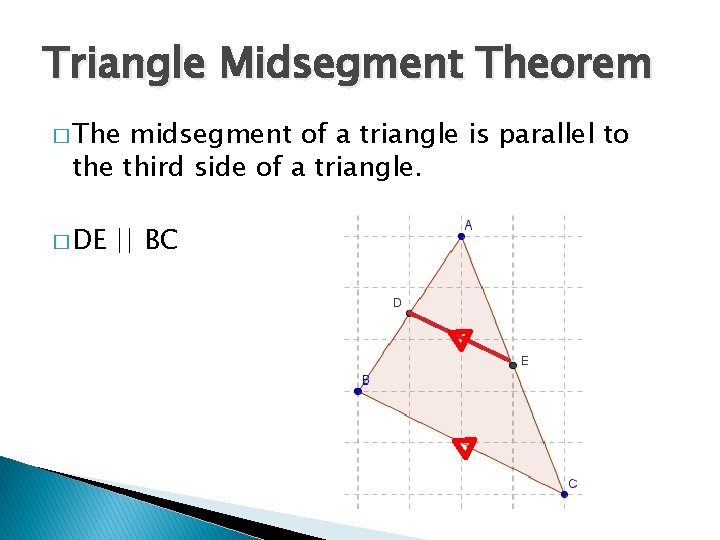
Triangle Midsegment Theorem � The midsegment of a triangle is parallel to the third side of a triangle. � DE || BC

Example 1 � Which segments are parallel?

Example 3 � M, N, and P are midpoint in ∆XYZ. The perimeter of ∆MNP is 60. Find NP and YZ. � MN = 22 MP = 24 � MN + MP + NP = 60 � 22 + 24 + NP = 60 � NP = 14 � XY = 28 � YZ = 44 � XZ = 48

Homework � 5. 1 Worksheet ◦ pg 262 #1 – 13 all

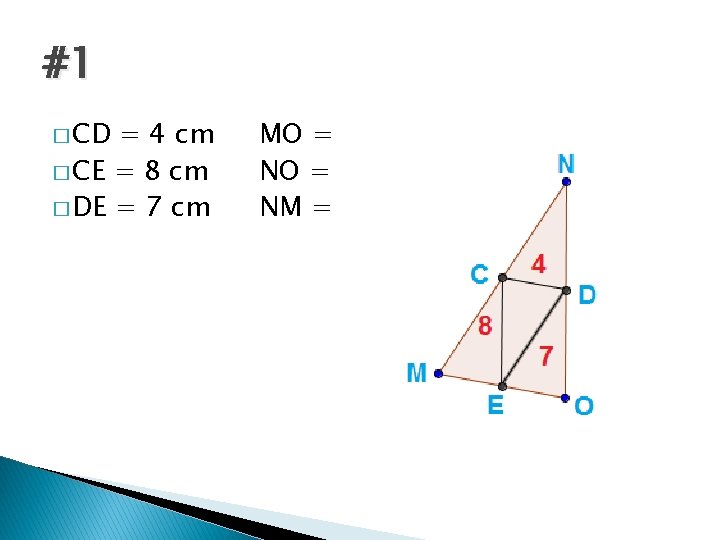
#1 � CD = 4 cm � CE = 8 cm � DE = 7 cm MO = NM =

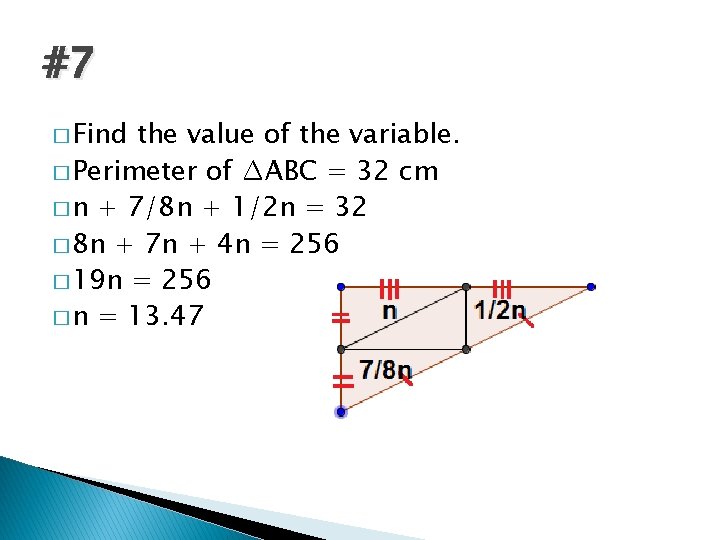
#7 � Find the value of the variable. � Perimeter of ∆ABC = 32 cm � n + 7/8 n + 1/2 n = 32 � 8 n + 7 n + 4 n = 256 � 19 n = 256 � n = 13. 47